高中数学人教A版必修2第三章 直线与方程3.2 直线的方程课件(28张PPT)
文档属性
| 名称 | 高中数学人教A版必修2第三章 直线与方程3.2 直线的方程课件(28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 06:38:30 | ||
图片预览








文档简介
复习
方程名称
已知条件
直线方程
使用范围
点
斜
式
斜
截
式
斜率k和直线在y轴上的截距
点
和斜率k
斜率必须存在
斜率不存在时,
解:设直线方程为:y=kx+b.
由已知得:
得:
所以,直线方程为: y=x+2
有其他做法吗?
所以,直线方程为: y=x+2
将A(1,3),k=1代入点斜式,
得: y-3= x-1
解:
x
y
l
P2(x2, y2)
P1(x1, y1)
O
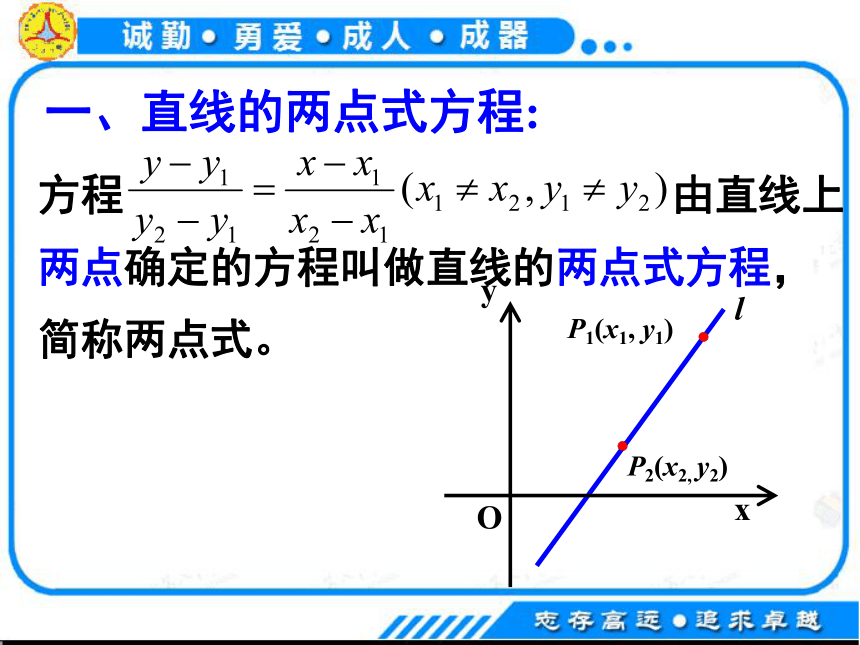
一、直线的两点式方程:
方程 由直线上两点确定的方程叫做直线的两点式方程,简称两点式。
x
y
l
P2(x2, y2)
P1(x1, y1)
O
三、直线的两点式方程的应用
不是!
两点式不能表示平行于坐标轴或与坐标轴重合的直线.
注意:
当x1 =x2或y1= y2时,直线P1 P2没有两点式程.(因为x1 =x2或y1= y2时,两点式的分母为零,没有意义)
那么两点式不能用来表示哪些直线的方程呢?
是不是已知任一直线中的两点就能用两点式
出直线方程呢?
新知拓展
记忆特点:
左边全为y,右边全为x
两边的分母全为常数
分子,分母中的减数相同
1.求经过下列两点的直线的两点式方程,再化斜截式方程.
(1)P(2,1),Q(0,-3)
(2)A(0,5),B(5,0)
(3)C(-4,-5),D(0,0)
(4)M(1,3),N(1,5)
课堂练习:
小结:两点式的优点和局限性?
例1:已知三角形的三个顶点A(-5, 0),
B(3, -3),C(0, 2),求:
(1)三角形三边所在直线的方程;
y
A
B
O
C
x
解:
直线AB
直线BC
直线AC
线段P1P2中P1(x1, y1), P2(x2, y2),
则中点P(x,y) :
x
y
P2(x2, y2)
P1(x1, y1)
O
中点坐标公式:
P (x, y)
在 中A(x1, y1), B(x2, y2), C(x3, y3),
则重心G(x,y) :
x
y
O
重心坐标公式:
G
A
B
C
例1:已知三角形的三个顶点A(-5, 0),
B(3, -3),C(0, 2),求:
(2)BC边上中线AM所在直线的方程;
y
A
B
O
C
x
解:
M
例1:已知三角形的三个顶点A(-5, 0),
B(3, -3),C(0, 2),求:
(3)BC边垂直平分线l所在直线的方程.
y
A
B
O
C
x
解:
M
l
截距式方程
x
y
l
A(a,0)
截距式方程
B(0,b)
代入两点式方程得
化简得
横截距
纵截距
截距式适用于横、纵截距都存在且都不为0的直线.
②截距可是正数,负数和零
①不能表示过原点或与坐标轴平行或重合的直线
是不是任意一条直线都有其截距式方程呢?
是不是都有截距呢?
注意:
截距式方程
2.根据下列条件求直线方程
(1)在x轴上的截距为2,在y轴上的截距是3;
(2)在x轴上的截距为-5,在y轴上的截距是6;
由截距式得: 整理得:
由截距式得: 整理得:
小结:截距式方程优点,局限?
3、根据下列条件,求直线的方程:
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2.
(三)典例分析
例2 教材P97 练习3T
⑴ 求过点P(2,3)并且在两个坐标轴上的截距相
等的直线有几条?
解:
例2:
斜率相等是否还有别的情况?
所以直线方程为:y=-x+5
解得:a=5
把(2,3)代入得:
设 直线的方程为:
两条
当直线截距都为零时,设直线方程为y=kx将点p(2,3)代入得:k=
所以直线方程为y= x
法二:设直线方程为:y-3=k(x-2)
令x=0,得y=-2k+3
令y=0,得x=
直线在坐标轴上的截距相等
2.求过点(4,-3)且在两坐标轴上截距的绝对值相等的直线l的方程.
自我提升:
(2)若直线l在两坐标轴上的截距相等,
则直线l的方程:
注:(1)截距式适用于与两坐标轴不垂直
且不过原点的直线。
x+y=a
或y=kx
(3)若直线l在两坐标轴上的截距互为相反数,
则直线l的方程:
x-y=a
或y=kx
(4)若直线l在两坐标轴上的截距绝对值相等,
则直线l的方程:
x+y=a
或y=kx
或x-y=a
名 称
几 何 条 件
方程
局限性
直线方程的四种具体形式
【总一总★成竹在胸】
数形结合与对称的灵活应用
已知一条光线从点A(2,-1)发出、经x轴反射后,
通过点B(-2,-4),试求点P坐标.
A(2,-1)
(x,0)
B(-2,-4)
P
变:已知两点A(2,-1)、B(-2,-4)
试在x轴上求一点P,使|PA|+|PB|最小
变:试在x轴上求一点P,使|PB|-|PA|最大
P(1.2,0)
P(1.2,0)
P(10\3,0)
数形结合与对称的灵活应用
已知直线l:x-2y+8=0和两点A(2,0)、B(-2,-4)
(1)求点A关于直线l的对称点
(2)在直线l是求一点P,使|PA|+|PB|最小
(3)在直线l是求一点Q,使| Q B|-| Q A|最大
A(2,0)
A1(x,y)
G
B(-2,-4)
P
A(2,0)
Q
B(-2,-4)
(-2,8)
(-2,3)
(12,10)
方程名称
已知条件
直线方程
使用范围
点
斜
式
斜
截
式
斜率k和直线在y轴上的截距
点
和斜率k
斜率必须存在
斜率不存在时,
解:设直线方程为:y=kx+b.
由已知得:
得:
所以,直线方程为: y=x+2
有其他做法吗?
所以,直线方程为: y=x+2
将A(1,3),k=1代入点斜式,
得: y-3= x-1
解:
x
y
l
P2(x2, y2)
P1(x1, y1)
O
一、直线的两点式方程:
方程 由直线上两点确定的方程叫做直线的两点式方程,简称两点式。
x
y
l
P2(x2, y2)
P1(x1, y1)
O
三、直线的两点式方程的应用
不是!
两点式不能表示平行于坐标轴或与坐标轴重合的直线.
注意:
当x1 =x2或y1= y2时,直线P1 P2没有两点式程.(因为x1 =x2或y1= y2时,两点式的分母为零,没有意义)
那么两点式不能用来表示哪些直线的方程呢?
是不是已知任一直线中的两点就能用两点式
出直线方程呢?
新知拓展
记忆特点:
左边全为y,右边全为x
两边的分母全为常数
分子,分母中的减数相同
1.求经过下列两点的直线的两点式方程,再化斜截式方程.
(1)P(2,1),Q(0,-3)
(2)A(0,5),B(5,0)
(3)C(-4,-5),D(0,0)
(4)M(1,3),N(1,5)
课堂练习:
小结:两点式的优点和局限性?
例1:已知三角形的三个顶点A(-5, 0),
B(3, -3),C(0, 2),求:
(1)三角形三边所在直线的方程;
y
A
B
O
C
x
解:
直线AB
直线BC
直线AC
线段P1P2中P1(x1, y1), P2(x2, y2),
则中点P(x,y) :
x
y
P2(x2, y2)
P1(x1, y1)
O
中点坐标公式:
P (x, y)
在 中A(x1, y1), B(x2, y2), C(x3, y3),
则重心G(x,y) :
x
y
O
重心坐标公式:
G
A
B
C
例1:已知三角形的三个顶点A(-5, 0),
B(3, -3),C(0, 2),求:
(2)BC边上中线AM所在直线的方程;
y
A
B
O
C
x
解:
M
例1:已知三角形的三个顶点A(-5, 0),
B(3, -3),C(0, 2),求:
(3)BC边垂直平分线l所在直线的方程.
y
A
B
O
C
x
解:
M
l
截距式方程
x
y
l
A(a,0)
截距式方程
B(0,b)
代入两点式方程得
化简得
横截距
纵截距
截距式适用于横、纵截距都存在且都不为0的直线.
②截距可是正数,负数和零
①不能表示过原点或与坐标轴平行或重合的直线
是不是任意一条直线都有其截距式方程呢?
是不是都有截距呢?
注意:
截距式方程
2.根据下列条件求直线方程
(1)在x轴上的截距为2,在y轴上的截距是3;
(2)在x轴上的截距为-5,在y轴上的截距是6;
由截距式得: 整理得:
由截距式得: 整理得:
小结:截距式方程优点,局限?
3、根据下列条件,求直线的方程:
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2.
(三)典例分析
例2 教材P97 练习3T
⑴ 求过点P(2,3)并且在两个坐标轴上的截距相
等的直线有几条?
解:
例2:
斜率相等是否还有别的情况?
所以直线方程为:y=-x+5
解得:a=5
把(2,3)代入得:
设 直线的方程为:
两条
当直线截距都为零时,设直线方程为y=kx将点p(2,3)代入得:k=
所以直线方程为y= x
法二:设直线方程为:y-3=k(x-2)
令x=0,得y=-2k+3
令y=0,得x=
直线在坐标轴上的截距相等
2.求过点(4,-3)且在两坐标轴上截距的绝对值相等的直线l的方程.
自我提升:
(2)若直线l在两坐标轴上的截距相等,
则直线l的方程:
注:(1)截距式适用于与两坐标轴不垂直
且不过原点的直线。
x+y=a
或y=kx
(3)若直线l在两坐标轴上的截距互为相反数,
则直线l的方程:
x-y=a
或y=kx
(4)若直线l在两坐标轴上的截距绝对值相等,
则直线l的方程:
x+y=a
或y=kx
或x-y=a
名 称
几 何 条 件
方程
局限性
直线方程的四种具体形式
【总一总★成竹在胸】
数形结合与对称的灵活应用
已知一条光线从点A(2,-1)发出、经x轴反射后,
通过点B(-2,-4),试求点P坐标.
A(2,-1)
(x,0)
B(-2,-4)
P
变:已知两点A(2,-1)、B(-2,-4)
试在x轴上求一点P,使|PA|+|PB|最小
变:试在x轴上求一点P,使|PB|-|PA|最大
P(1.2,0)
P(1.2,0)
P(10\3,0)
数形结合与对称的灵活应用
已知直线l:x-2y+8=0和两点A(2,0)、B(-2,-4)
(1)求点A关于直线l的对称点
(2)在直线l是求一点P,使|PA|+|PB|最小
(3)在直线l是求一点Q,使| Q B|-| Q A|最大
A(2,0)
A1(x,y)
G
B(-2,-4)
P
A(2,0)
Q
B(-2,-4)
(-2,8)
(-2,3)
(12,10)
