高中数学人教A版必修3课件-2.2.2用样本的数字特征估计总体的数字特征(1)(28张PPT)
文档属性
| 名称 | 高中数学人教A版必修3课件-2.2.2用样本的数字特征估计总体的数字特征(1)(28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 06:49:55 | ||
图片预览





文档简介
0.0001
0.0002
0.0003
0.0004
0.0005
1000 1500 2000 2500 3000 3500 4000
月收入(元)
频率/组距
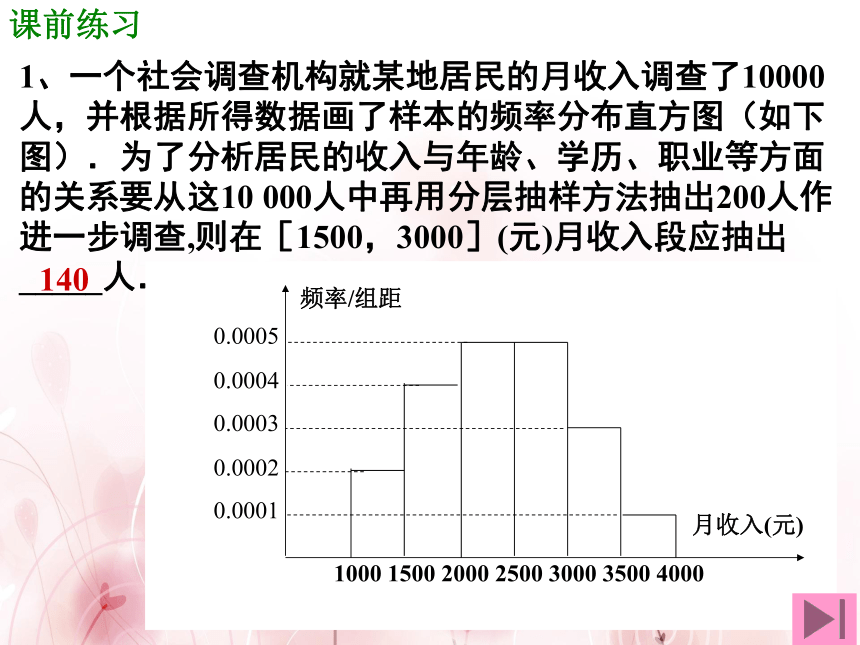
1、一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系要从这10 000人中再用分层抽样方法抽出200人作进一步调查,则在[1500,3000](元)月收入段应抽出_____人.
140
课前练习
2、一个容量为40的样本数据分组后组数与频数如下:
[25,25.3),6;[25.3,25.6),4;[25.6,25.9),10;
[25.9,26.2),8;[26.2,26.5),8;[26.5,26.8),4;
则样本在[25,25.9)上的频率为( )
C
课前练习
⑵中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
⑴众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.
众数、中位数、平均数都是描述一组数据的集中趋势的特征数,只是描述的角度不同,其中以平均数的应用最为广泛.
⑶平均数:一组数据的算术平均数,即
一、基础知识讲解
(一)基本概念
(二)众数、中位数、平均数与频率分布直方图的关系
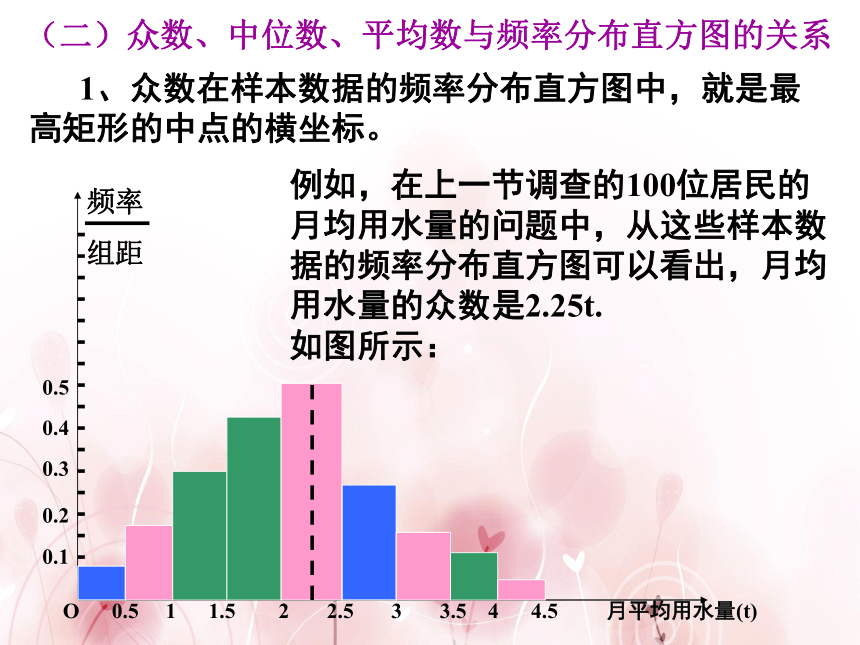
1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。
频率
组距
0.1
0.2
0.3
0.4
0.5
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)
例如,在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.
如图所示:
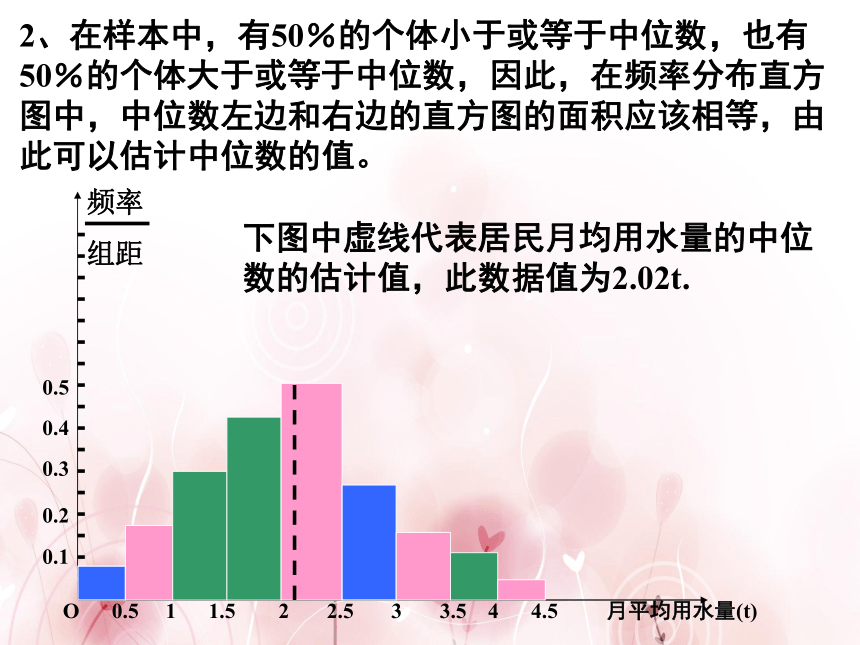
2、在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。
频率
组距
0.1
0.2
0.3
0.4
0.5
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)
下图中虚线代表居民月均用水量的中位数的估计值,此数据值为2.02t.
说明:
2.02这个中位数的估计值,与样本的中位数值2.0不一样,这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致。
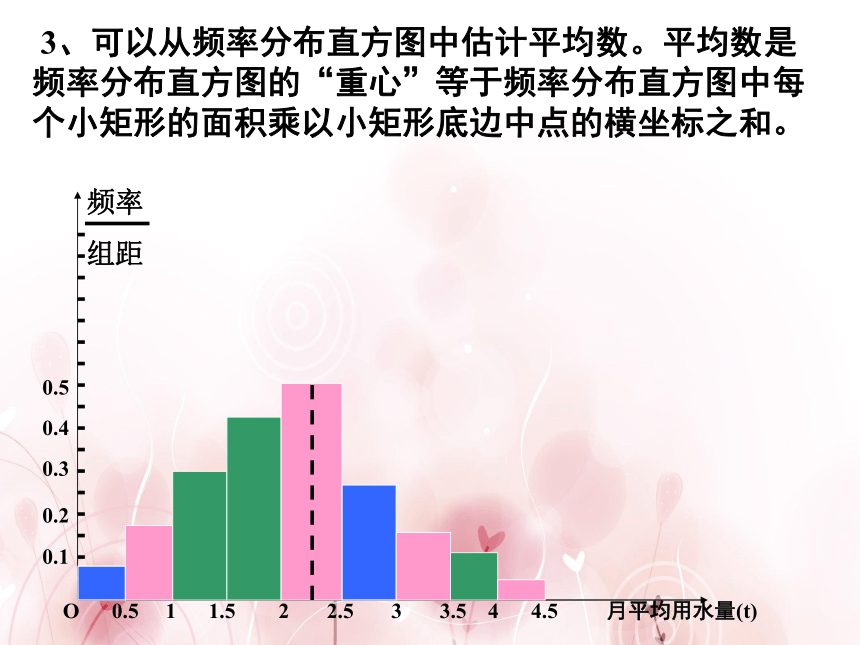
3、可以从频率分布直方图中估计平均数。平均数是频率分布直方图的“重心”等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
频率
组距
0.1
0.2
0.3
0.4
0.5
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)
(三)三种数字特征的优缺点
⑴众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征。如上例中众数是2.25t,它告诉我们,月均用水量为2.25t的居民数比月均用水量为其它数值的居民数多,但它并没有告诉我们多多少。
⑵中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点。如上例中假设有某一用户月均用水量为10t,那么它所占频率为0.01,几乎不影响中位数,但显然这一极端值是不能忽视的。
⑶由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。也正因如此 ,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。
例1、某工厂人员及工资构成如下:
人员
经理
管理人员
高级技工
工人
学徒
合计
周工资
2200
250
220
200
100
人数
1
6
5
10
1
23
合计
2200
1500
1100
2000
100
6900
(1)指出这个问题中周工资的众数、中位数、平均数。
(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么?
二、应用举例
分析:众数为200,中位数为220,平均数为300。
因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平。
有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
问题:如果你是教练,你应当如何对这次射击作出评价?
如果看两人本次射击的平均成绩,由于
两人射击的平均成绩是一样的。那么两个人的水平就没有什么差异吗?
平均数向我们提供了样本数据的重要信息,但是平均数有时也会使我们作出对总体的片面判断。因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽略的。因此,只有平均数还难以概括样本数据的实际状态。
(四)标准差
4
5
6
7
8
9
10
环数
频率
0.1
0.2
0.3
(甲)
4
5
6
7
8
9
10
0.1
0.2
0.3
0.4
环数
频率
(乙)
直观上看,还是有差异的。如:甲成绩比较分散,乙成绩相对集中(如图示)。
即甲、乙的成绩相对于他们的平均成绩的离散程度不同。
在数学中,刻画数据相对于平均数的离散程度,经常
用标准差或方差
表示这组数据的标准差
直观上看,还是有差异的。如:甲成绩比较分散,乙成绩相对集中(如图示)。因此,我们还需要从另外的角度来考察这两组。例如:在作统计图、表时提到过的极差。
甲的环数极差=10-4=6
乙的环数极差=9-5=4.
考察样本数据的分散程度的大小,最常用的统计量是标准差.标准差是样本平均数的一种平均距离,一般用s表示.
所谓“平均距离”,其含义可作如下理解:
由于上式含有绝对值,运算不太方便,因此,通常改用如下公式来计算标准差
(四)标准差
由 可以知道,甲的成绩离散程度大,乙的成绩离散程度小.由此可以估计,乙比甲的射击成绩稳定.
显然,标准差越大,则a越大,数据的离散程度越大;标准差越小,数据的离散程度越小。
用计算器可得
上面两组数据的离散程度与标准差之间的关系可用图直观地表示出来.
4
5
6
7
8
9
10
a
一个样本中的个体与平均数之间的距离关系可用下图表示:
考虑一个容量为2的样本:
例2、画出下列四组样本数据的条形图,说明它们的异同点.
(1) 5,5,5,5,5,5,5,5,5;
(2) 4,4,4,5,5,5,6,6,6;
(3) 3,3,4,4,5,6,6,7,7;
(4) 2,2,2,2,5,8,8,8,8;
解:四组样本数据的条形图是:
二、应用举例
S=0.00
频率
o
1
2
3
4
5
6
7
8
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
(1)
S=0.82
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
(2)
频率
o
1
2
3
4
5
6
7
8
S=1.49
S=2.83
四组数据的平均数都是5.0,标准差分别是0.00,0.82,1.49,2.83。
虽然它们有相同的平均数,但是它们有不同的标准差,说明数据的分散程度是不一样的。
1
2
3
4
5
6
7
8
频率
o
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
(3)
频率
o
1
2
3
4
5
6
7
8
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
(4)
标准差还可以用于对样本数据的另外一种解释。例如,在关于居民月均用水量的例子中,平均数:
标准差s=0.868 ,所以
例2、甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm)
甲 25.46, 25.32, 25.45, 25.39, 25.36
25.34, 25.42, 25.45, 25.38, 25.42
25.39, 25.43, 25.39, 25.40, 25.44
25.40, 25.42, 25.35, 25.41, 25.39
乙 25.40, 25.43, 25.44, 25.48, 25.48
25.47, 25.49, 25.49, 25.36, 25.34
25.33, 25.43, 25.43, 25.32, 25.47
25.31, 25.32, 25.32, 25.32, 25.48
从生产的零件内径的尺寸看,谁生产的质量较高?
解:用计算器计算可得:
从样本平均数看,甲生产的零件内径比乙生产的更接近内径标准(25.40mm),但是差异很小;从样本标准差看,由于:
例3、求下列数据的标准差和方差
(1)5,7,7,8,10,11
(2)10,14,14,16,20,22
(3)7,9,9,10,12,13
B
四、针对性练习
2、已知一组数据为-1, 0, 4, x , 6, 15, 且这组数据的中位数为5, 那么这组数据的众数为( )
A、4 B、5 C、6 D、15
C
3、如果一组数中每个数加上同一个非零常数,则这一组数的( ).
A、平均数不变,标准差不变
B、平均数改变,标准差改变
C、平均数不变,标准差改变
D、平均数改变,标准差不变
D
四、针对性练习
C
16
6
四、针对性练习
96
四、针对性练习
2.标准差计算公式
3.方差计算公式
1.学会从频率分布直方图中估计众数、中位数、平均数
五、课时小结
0.0002
0.0003
0.0004
0.0005
1000 1500 2000 2500 3000 3500 4000
月收入(元)
频率/组距
1、一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系要从这10 000人中再用分层抽样方法抽出200人作进一步调查,则在[1500,3000](元)月收入段应抽出_____人.
140
课前练习
2、一个容量为40的样本数据分组后组数与频数如下:
[25,25.3),6;[25.3,25.6),4;[25.6,25.9),10;
[25.9,26.2),8;[26.2,26.5),8;[26.5,26.8),4;
则样本在[25,25.9)上的频率为( )
C
课前练习
⑵中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
⑴众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.
众数、中位数、平均数都是描述一组数据的集中趋势的特征数,只是描述的角度不同,其中以平均数的应用最为广泛.
⑶平均数:一组数据的算术平均数,即
一、基础知识讲解
(一)基本概念
(二)众数、中位数、平均数与频率分布直方图的关系
1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。
频率
组距
0.1
0.2
0.3
0.4
0.5
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)
例如,在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.
如图所示:
2、在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。
频率
组距
0.1
0.2
0.3
0.4
0.5
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)
下图中虚线代表居民月均用水量的中位数的估计值,此数据值为2.02t.
说明:
2.02这个中位数的估计值,与样本的中位数值2.0不一样,这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致。
3、可以从频率分布直方图中估计平均数。平均数是频率分布直方图的“重心”等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
频率
组距
0.1
0.2
0.3
0.4
0.5
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)
(三)三种数字特征的优缺点
⑴众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征。如上例中众数是2.25t,它告诉我们,月均用水量为2.25t的居民数比月均用水量为其它数值的居民数多,但它并没有告诉我们多多少。
⑵中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点。如上例中假设有某一用户月均用水量为10t,那么它所占频率为0.01,几乎不影响中位数,但显然这一极端值是不能忽视的。
⑶由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。也正因如此 ,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。
例1、某工厂人员及工资构成如下:
人员
经理
管理人员
高级技工
工人
学徒
合计
周工资
2200
250
220
200
100
人数
1
6
5
10
1
23
合计
2200
1500
1100
2000
100
6900
(1)指出这个问题中周工资的众数、中位数、平均数。
(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么?
二、应用举例
分析:众数为200,中位数为220,平均数为300。
因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平。
有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
问题:如果你是教练,你应当如何对这次射击作出评价?
如果看两人本次射击的平均成绩,由于
两人射击的平均成绩是一样的。那么两个人的水平就没有什么差异吗?
平均数向我们提供了样本数据的重要信息,但是平均数有时也会使我们作出对总体的片面判断。因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽略的。因此,只有平均数还难以概括样本数据的实际状态。
(四)标准差
4
5
6
7
8
9
10
环数
频率
0.1
0.2
0.3
(甲)
4
5
6
7
8
9
10
0.1
0.2
0.3
0.4
环数
频率
(乙)
直观上看,还是有差异的。如:甲成绩比较分散,乙成绩相对集中(如图示)。
即甲、乙的成绩相对于他们的平均成绩的离散程度不同。
在数学中,刻画数据相对于平均数的离散程度,经常
用标准差或方差
表示这组数据的标准差
直观上看,还是有差异的。如:甲成绩比较分散,乙成绩相对集中(如图示)。因此,我们还需要从另外的角度来考察这两组。例如:在作统计图、表时提到过的极差。
甲的环数极差=10-4=6
乙的环数极差=9-5=4.
考察样本数据的分散程度的大小,最常用的统计量是标准差.标准差是样本平均数的一种平均距离,一般用s表示.
所谓“平均距离”,其含义可作如下理解:
由于上式含有绝对值,运算不太方便,因此,通常改用如下公式来计算标准差
(四)标准差
由 可以知道,甲的成绩离散程度大,乙的成绩离散程度小.由此可以估计,乙比甲的射击成绩稳定.
显然,标准差越大,则a越大,数据的离散程度越大;标准差越小,数据的离散程度越小。
用计算器可得
上面两组数据的离散程度与标准差之间的关系可用图直观地表示出来.
4
5
6
7
8
9
10
a
一个样本中的个体与平均数之间的距离关系可用下图表示:
考虑一个容量为2的样本:
例2、画出下列四组样本数据的条形图,说明它们的异同点.
(1) 5,5,5,5,5,5,5,5,5;
(2) 4,4,4,5,5,5,6,6,6;
(3) 3,3,4,4,5,6,6,7,7;
(4) 2,2,2,2,5,8,8,8,8;
解:四组样本数据的条形图是:
二、应用举例
S=0.00
频率
o
1
2
3
4
5
6
7
8
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
(1)
S=0.82
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
(2)
频率
o
1
2
3
4
5
6
7
8
S=1.49
S=2.83
四组数据的平均数都是5.0,标准差分别是0.00,0.82,1.49,2.83。
虽然它们有相同的平均数,但是它们有不同的标准差,说明数据的分散程度是不一样的。
1
2
3
4
5
6
7
8
频率
o
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
(3)
频率
o
1
2
3
4
5
6
7
8
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
(4)
标准差还可以用于对样本数据的另外一种解释。例如,在关于居民月均用水量的例子中,平均数:
标准差s=0.868 ,所以
例2、甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm)
甲 25.46, 25.32, 25.45, 25.39, 25.36
25.34, 25.42, 25.45, 25.38, 25.42
25.39, 25.43, 25.39, 25.40, 25.44
25.40, 25.42, 25.35, 25.41, 25.39
乙 25.40, 25.43, 25.44, 25.48, 25.48
25.47, 25.49, 25.49, 25.36, 25.34
25.33, 25.43, 25.43, 25.32, 25.47
25.31, 25.32, 25.32, 25.32, 25.48
从生产的零件内径的尺寸看,谁生产的质量较高?
解:用计算器计算可得:
从样本平均数看,甲生产的零件内径比乙生产的更接近内径标准(25.40mm),但是差异很小;从样本标准差看,由于:
例3、求下列数据的标准差和方差
(1)5,7,7,8,10,11
(2)10,14,14,16,20,22
(3)7,9,9,10,12,13
B
四、针对性练习
2、已知一组数据为-1, 0, 4, x , 6, 15, 且这组数据的中位数为5, 那么这组数据的众数为( )
A、4 B、5 C、6 D、15
C
3、如果一组数中每个数加上同一个非零常数,则这一组数的( ).
A、平均数不变,标准差不变
B、平均数改变,标准差改变
C、平均数不变,标准差改变
D、平均数改变,标准差不变
D
四、针对性练习
C
16
6
四、针对性练习
96
四、针对性练习
2.标准差计算公式
3.方差计算公式
1.学会从频率分布直方图中估计众数、中位数、平均数
五、课时小结
