高中数学人教A版选修2-1第三章3.2立体几何中的向量法 课件(28张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-1第三章3.2立体几何中的向量法 课件(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 06:53:50 | ||
图片预览







文档简介
立体几何中的向量方法
学习目标:
1、理解直线的方向向量和平面的法向量;
2、能用向量语言表达线线、线面、面面的平行和垂直关系;
3、能用向量法解决直线与直线、直线与平面、平面与平面的夹角问题;
4、会用向量法求两异面直线和点到平面之间的距离。
?
一、空间两点间的距离公式
?
?
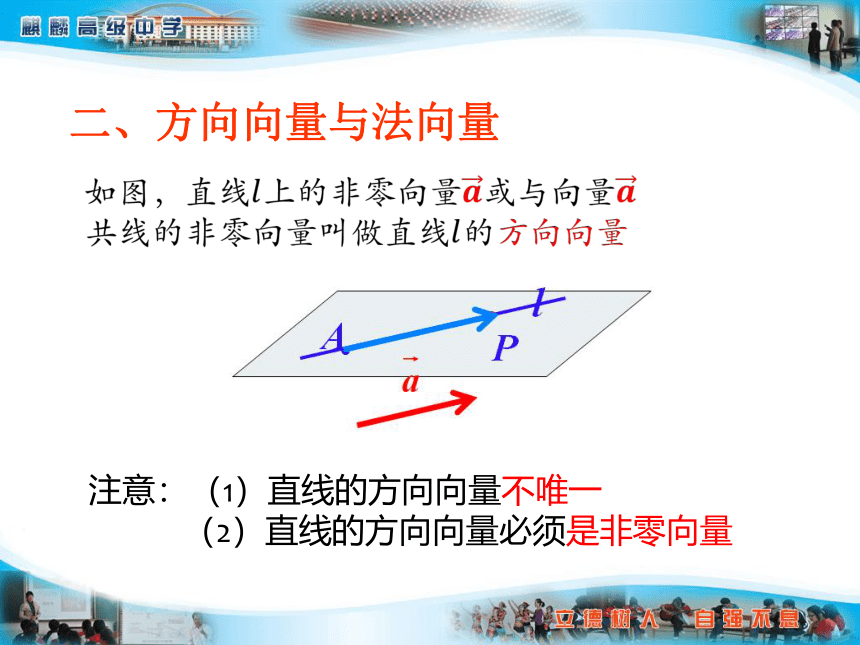
二、方向向量与法向量
?
注意:(1)直线的方向向量不唯一
(2)直线的方向向量必须是非零向量
?
?
例1. 如图所示, 正方体的棱长为1
直线OA的一个方向向量坐标为___________
平面OABC 的一个法向量坐标为___________
平面AB1C 的一个法向量坐标为___________
(-1,-1,1)
(0,0,1)
(1,0,0)
?
?
注意:法向量不唯一
?
例2.在空间直角坐标系中,已知A(3,0,0),
B(0,4,0),C(0,0,2),试求平面ABC的
一个法向量.
?
?
三、直线与平面、平面与平面的平行与垂直的判断
?
?
1、线面平行
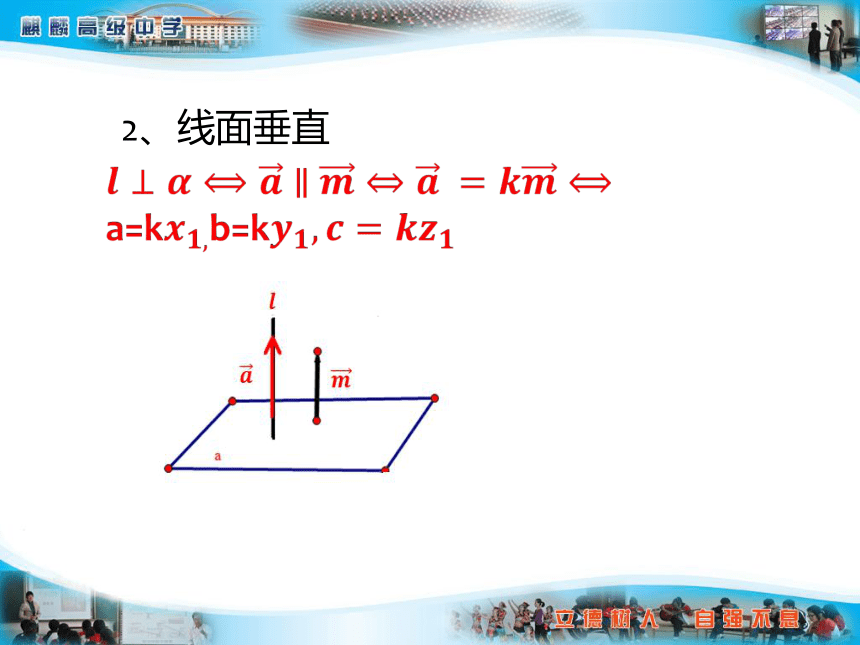
2、线面垂直
?
3、面面平行
?
4、面面垂直
?
四、利用向量求空间的角
1、异面直线所成角
?
?
?
例:如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB,A1D1的中点,求直线EF与BD1所成角的余弦值。
?
?
?
2、直线与平面所成角
?
?
?
?
(2)试问:在棱AD上是否存在点M,使得BM与平面PAD所成角为45°?若存在,求AM的长度;若不存在,说明理由.
?
?
?
?
3、二面角
?
?
?
?
?
?
?
因为二面角为锐二面角
五、空间的距离
1、两异面直线之间的距离
?
?
?
?
?
解:如图,以点D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直坐标系O-xyz.
?
?
?
?
?
取y=2,的x=5,z=1
?
?
?
2、点到平面的距离
?
?
?
?
解:如图,以点D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直坐标系O-xyz.
?
?
?
取x=1,得y=1,z=1
?
?
设点A到平面PQL的距离为d
?
三角
线线所成角,余弦不要绝对值;
线面所成角,正弦加上绝对值;
面面所成角,余弦加上绝对值,
若要去掉绝对值,符号看图来决定!
两距离
线线之间的距离,公垂向量是关键;两线各取一个点,连线之后找投影;点面之间的距离,先来求出法向量,平面之内任取点,点点连线找投影!
课堂小结:
学习目标:
1、理解直线的方向向量和平面的法向量;
2、能用向量语言表达线线、线面、面面的平行和垂直关系;
3、能用向量法解决直线与直线、直线与平面、平面与平面的夹角问题;
4、会用向量法求两异面直线和点到平面之间的距离。
?
一、空间两点间的距离公式
?
?
二、方向向量与法向量
?
注意:(1)直线的方向向量不唯一
(2)直线的方向向量必须是非零向量
?
?
例1. 如图所示, 正方体的棱长为1
直线OA的一个方向向量坐标为___________
平面OABC 的一个法向量坐标为___________
平面AB1C 的一个法向量坐标为___________
(-1,-1,1)
(0,0,1)
(1,0,0)
?
?
注意:法向量不唯一
?
例2.在空间直角坐标系中,已知A(3,0,0),
B(0,4,0),C(0,0,2),试求平面ABC的
一个法向量.
?
?
三、直线与平面、平面与平面的平行与垂直的判断
?
?
1、线面平行
2、线面垂直
?
3、面面平行
?
4、面面垂直
?
四、利用向量求空间的角
1、异面直线所成角
?
?
?
例:如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB,A1D1的中点,求直线EF与BD1所成角的余弦值。
?
?
?
2、直线与平面所成角
?
?
?
?
(2)试问:在棱AD上是否存在点M,使得BM与平面PAD所成角为45°?若存在,求AM的长度;若不存在,说明理由.
?
?
?
?
3、二面角
?
?
?
?
?
?
?
因为二面角为锐二面角
五、空间的距离
1、两异面直线之间的距离
?
?
?
?
?
解:如图,以点D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直坐标系O-xyz.
?
?
?
?
?
取y=2,的x=5,z=1
?
?
?
2、点到平面的距离
?
?
?
?
解:如图,以点D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直坐标系O-xyz.
?
?
?
取x=1,得y=1,z=1
?
?
设点A到平面PQL的距离为d
?
三角
线线所成角,余弦不要绝对值;
线面所成角,正弦加上绝对值;
面面所成角,余弦加上绝对值,
若要去掉绝对值,符号看图来决定!
两距离
线线之间的距离,公垂向量是关键;两线各取一个点,连线之后找投影;点面之间的距离,先来求出法向量,平面之内任取点,点点连线找投影!
课堂小结:
