沪教版(上海)数学高二下册-11.1 直线的点方向式方程课件(25张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二下册-11.1 直线的点方向式方程课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 578.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 20:59:19 | ||
图片预览




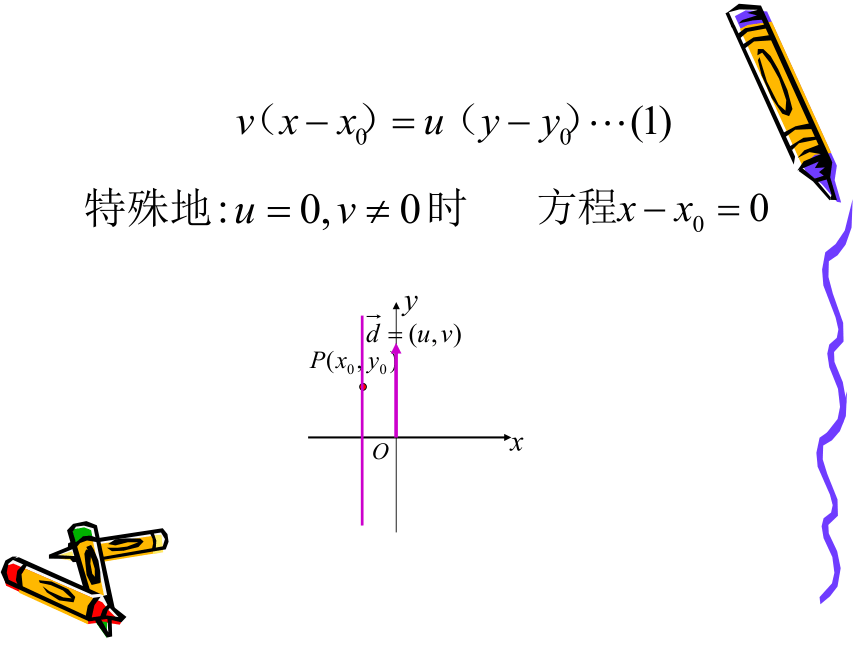
文档简介
直线的点方向式方程
教学目标:
知识与技能:
理解直线方程的意义,掌握直线的点方向式方程。
过程与方法:
学生分类讨论、数形结合等数学思想和探究能力
的培养。
情感态度与价值观:
培养学生探究新事物的欲望,获得成功的体验,
树立学好数学的信心。
教学重点:
直线的点方向式方程。
教学难点:
理解直线方程以及点方向式方程的推导。
直线的点方向式方程
现实世界中到处有美妙的曲线,……这些曲线和方程息息相关。
引进直角坐标系,把图像上的点用有序实数对(x,y)来表示。就可以根据曲线的几何性质可以得到一个关于x,y的代数方程f(x,y)=0
南浦大桥1
南浦大桥2
南浦大桥3
长江隧桥1
长江隧桥2
南浦大桥4
x
y
o
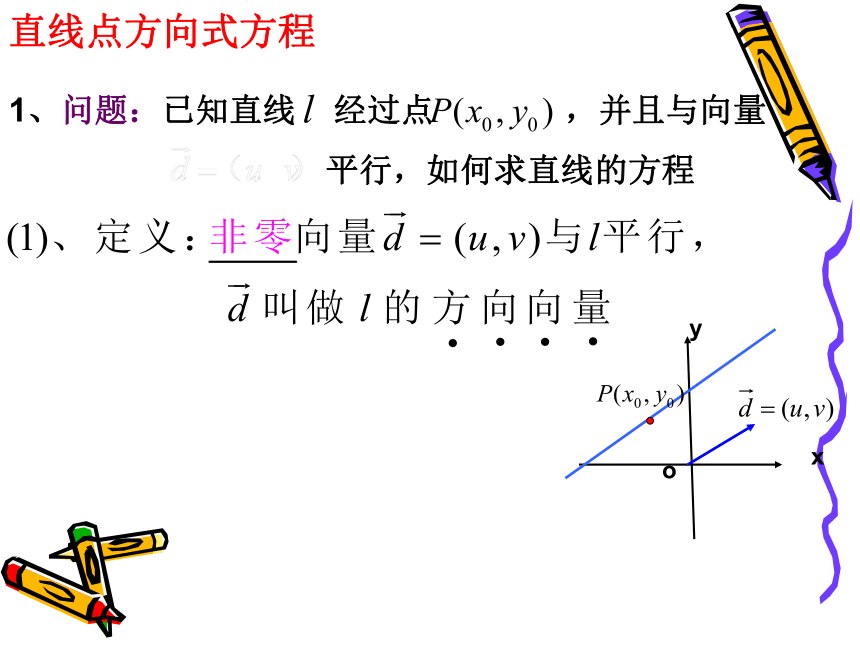
直线点方向式方程
1、问题:已知直线 经过点 ,并且与向量
平行,如何求直线的方程
x
y
o
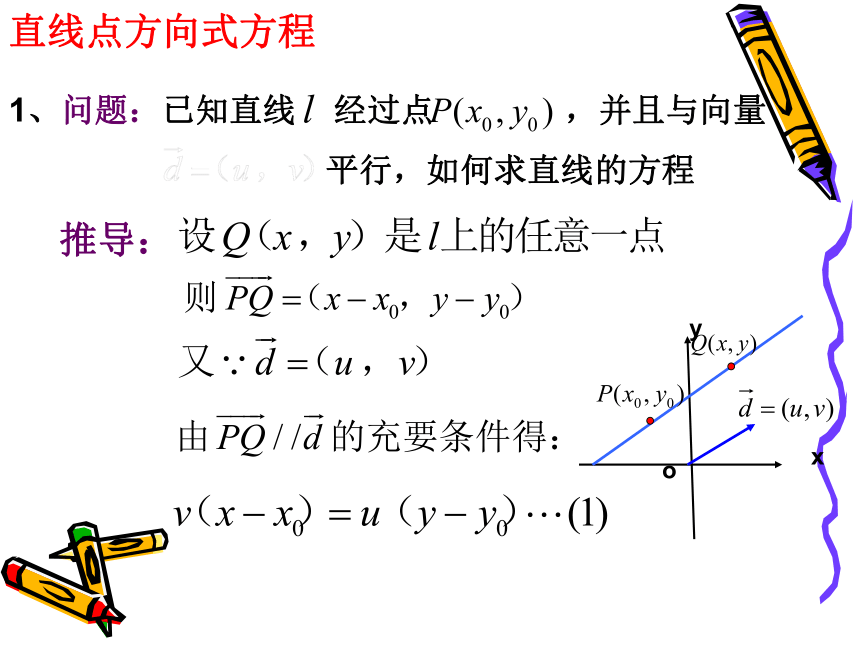
直线点方向式方程
1、问题:已知直线 经过点 ,并且与向量
平行,如何求直线的方程
推导:
这条直线 就叫做这个方程(1)的图形
这个方程(1)就叫做这条直线 的方程
方程与直线的关系
直线的点方向式方程
应用举例
例1:观察下列直线方程,并指出各直线必过
的点和它的一个方向向量?
例3、已知A(4,6)、B(-3,-1)、C(4,-5)
x
y
o
求经过点A且与BC平行的直线 的点方向式方程
直线 经过
解:
它的一个方向向量
所以,直线 的点方向式方程为
1、已知A(4,6)、B(-3,-1)、C(4,-5)
求经过点B且与AC平行的直线 的方程
2、已知A(4,6)、B(-3,-1)、C(4,-5)
求经过点C且与AB平行的直线 的点方向式方程
课堂练习:
变式1、已知A(4,6)、B(-3,-1)、C(4,-5)
x
y
o
求经过B、C两点的直线 的点方向式方程
因为直线 经过B、C两点,
它的一个方向向量为
所以直线 的点方向式方程
解:
思考
变式2、已知A(4,6)、B(-3,-1)、C(4,-5)
x
y
o
求 中,平行于BC边的中位线MN所在的直线的点方向式方程
解:
AB的中点为
AC的中点为
则
所以,MN所在的直线的点方向式方程是
MN
变式3、已知A(4,6)、B(-3,-1)、C(4,-5)
x
y
o
求 中,BC边的中线所在的直线的点方向式方程
BC的中点为
则
所以,直线AD的点方向式方程是
解:
如图:依题意可知,AD为所求的直线
拓展
能否把直线 化成点方向式方程?
若能,它的点方式方程是否唯一?
并观察x,y的系数与方向向量有什么联系?
小结
探索
直线 的方向向量可以表示为?
我们通过对现实生活中的直线的图片,引入直线,然后抽象成数学意义上的直线,接下来我们把这个几何图形通过坐标的形式转化成代数问题,然后通过方程来研究直线!
课堂小结:
思考:我们这节课重点学习了
哪种直线方程?
思考:它的表示形式是?
如果代数与几何各自分开发展,那它进步将十分缓慢,而且应用范围也很有限。但若两者互相结合而共同发展,则就会相互加强,并以快速的步伐向着完美化的方向猛进。 —— 拉格朗日
家庭作业
数学练习册:
变式2、已知A(4,6)、B(-3,-1)、C(4,-5)
x
y
o
求 中,平行于BC边的中位线MN所在的直线的点方向式方程
解:
AB的中点为
AC的中点为
则
所以,MN所在的直线的点方向式方程是
返回
1本节课所做的幻灯片的内容是2课时的内容,如果上一堂课 ,可酌情删
减。
2从变式1或变式3还可以总结出这样一个结论:过两点 的
点方向式方程为:
3从变式1中验证了,代入B或C点之后,所得到的点方向式的表现形式虽
然不同,但化简后的实质却是同一个方程,由此可见,直线确定后,虽
有无数个点,但具有的特征确实相同的--均为直线的特征。
4从变式2的方向向量BC与MN的不同(BC=2MN),所得到的直线方程的
点方向式方程的形式也出现了不同之处,但与变式1相比,更容易看出
是一条直线,方程的两边只要乘上一个系数可以相互转化。
5拓展先看特例向量
教学后记:
教学目标:
知识与技能:
理解直线方程的意义,掌握直线的点方向式方程。
过程与方法:
学生分类讨论、数形结合等数学思想和探究能力
的培养。
情感态度与价值观:
培养学生探究新事物的欲望,获得成功的体验,
树立学好数学的信心。
教学重点:
直线的点方向式方程。
教学难点:
理解直线方程以及点方向式方程的推导。
直线的点方向式方程
现实世界中到处有美妙的曲线,……这些曲线和方程息息相关。
引进直角坐标系,把图像上的点用有序实数对(x,y)来表示。就可以根据曲线的几何性质可以得到一个关于x,y的代数方程f(x,y)=0
南浦大桥1
南浦大桥2
南浦大桥3
长江隧桥1
长江隧桥2
南浦大桥4
x
y
o
直线点方向式方程
1、问题:已知直线 经过点 ,并且与向量
平行,如何求直线的方程
x
y
o
直线点方向式方程
1、问题:已知直线 经过点 ,并且与向量
平行,如何求直线的方程
推导:
这条直线 就叫做这个方程(1)的图形
这个方程(1)就叫做这条直线 的方程
方程与直线的关系
直线的点方向式方程
应用举例
例1:观察下列直线方程,并指出各直线必过
的点和它的一个方向向量?
例3、已知A(4,6)、B(-3,-1)、C(4,-5)
x
y
o
求经过点A且与BC平行的直线 的点方向式方程
直线 经过
解:
它的一个方向向量
所以,直线 的点方向式方程为
1、已知A(4,6)、B(-3,-1)、C(4,-5)
求经过点B且与AC平行的直线 的方程
2、已知A(4,6)、B(-3,-1)、C(4,-5)
求经过点C且与AB平行的直线 的点方向式方程
课堂练习:
变式1、已知A(4,6)、B(-3,-1)、C(4,-5)
x
y
o
求经过B、C两点的直线 的点方向式方程
因为直线 经过B、C两点,
它的一个方向向量为
所以直线 的点方向式方程
解:
思考
变式2、已知A(4,6)、B(-3,-1)、C(4,-5)
x
y
o
求 中,平行于BC边的中位线MN所在的直线的点方向式方程
解:
AB的中点为
AC的中点为
则
所以,MN所在的直线的点方向式方程是
MN
变式3、已知A(4,6)、B(-3,-1)、C(4,-5)
x
y
o
求 中,BC边的中线所在的直线的点方向式方程
BC的中点为
则
所以,直线AD的点方向式方程是
解:
如图:依题意可知,AD为所求的直线
拓展
能否把直线 化成点方向式方程?
若能,它的点方式方程是否唯一?
并观察x,y的系数与方向向量有什么联系?
小结
探索
直线 的方向向量可以表示为?
我们通过对现实生活中的直线的图片,引入直线,然后抽象成数学意义上的直线,接下来我们把这个几何图形通过坐标的形式转化成代数问题,然后通过方程来研究直线!
课堂小结:
思考:我们这节课重点学习了
哪种直线方程?
思考:它的表示形式是?
如果代数与几何各自分开发展,那它进步将十分缓慢,而且应用范围也很有限。但若两者互相结合而共同发展,则就会相互加强,并以快速的步伐向着完美化的方向猛进。 —— 拉格朗日
家庭作业
数学练习册:
变式2、已知A(4,6)、B(-3,-1)、C(4,-5)
x
y
o
求 中,平行于BC边的中位线MN所在的直线的点方向式方程
解:
AB的中点为
AC的中点为
则
所以,MN所在的直线的点方向式方程是
返回
1本节课所做的幻灯片的内容是2课时的内容,如果上一堂课 ,可酌情删
减。
2从变式1或变式3还可以总结出这样一个结论:过两点 的
点方向式方程为:
3从变式1中验证了,代入B或C点之后,所得到的点方向式的表现形式虽
然不同,但化简后的实质却是同一个方程,由此可见,直线确定后,虽
有无数个点,但具有的特征确实相同的--均为直线的特征。
4从变式2的方向向量BC与MN的不同(BC=2MN),所得到的直线方程的
点方向式方程的形式也出现了不同之处,但与变式1相比,更容易看出
是一条直线,方程的两边只要乘上一个系数可以相互转化。
5拓展先看特例向量
教学后记:
