沪教版(上海)数学高二下册-11.3 两条直线的位置关系 课件(21张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二下册-11.3 两条直线的位置关系 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 425.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 21:05:13 | ||
图片预览






文档简介
两条直线的位置关系
1. 点与直线位置关系
存在点到直线的最短距离
2. 直线与直线位置关系
在同一平面上的直线之间,有相交、平行、重合三种位置关系,那么这三种位置关系反映在直线方程关系上如何呢?
设直角坐标系上两条直线的方程分别为:
结论:
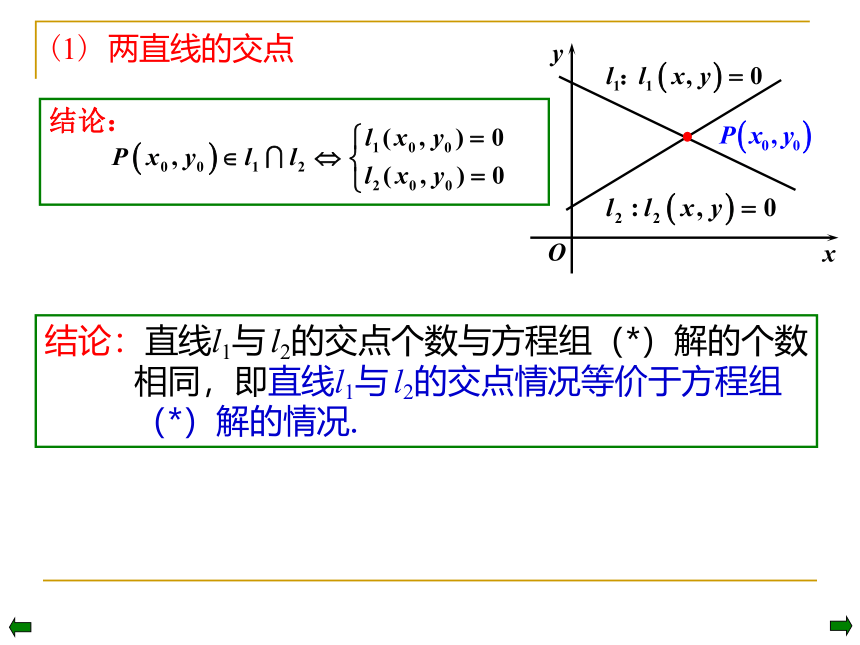
结论:直线l1与 l2的交点个数与方程组(*)解的个数相同,即直线l1与 l2的交点情况等价于方程组(*)解的情况.
(1) 两直线的交点
(2)两直线的位置关系
方程组(*)有唯一解
即直线l1与 l2相交于一点,其交点坐标是
设直角坐标系上两条直线的方程分别为:
方程组(*)无解
即直线 l1// l2
方程组(*)有无穷多解
即直线l1与 l2重合
结论:D=0 即a1b2-a2b1=0 是直线l1与 l2平行或重合的必要条件.
特别地:
特别地
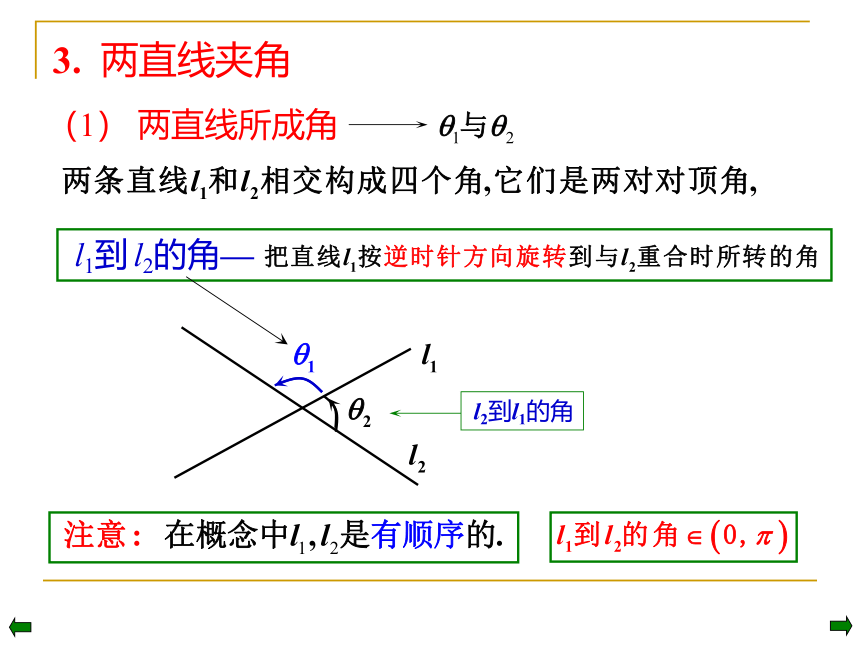
l1到 l2的角—
3. 两直线夹角
(1) 两直线所成角
l2到l1的角
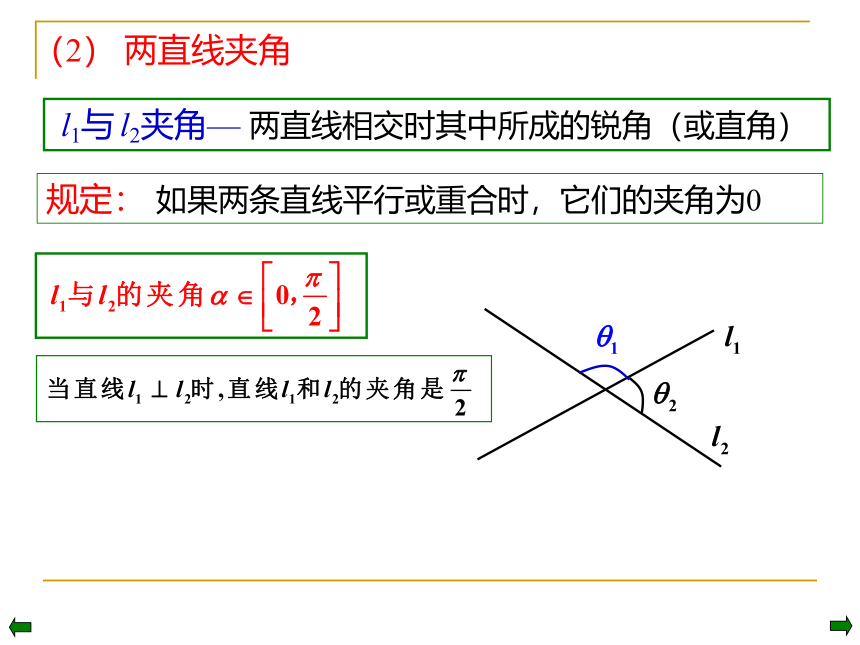
(2) 两直线夹角
l1与 l2夹角— 两直线相交时其中所成的锐角(或直角)
规定: 如果两条直线平行或重合时,它们的夹角为0
(3) 两直线夹角公式
设两条直线l1与l2的方程分别为:
(4) 两直线夹角正切公式
(1)
(2)
x
y
O
O
y
x
x
y
O
x
y
O
解:
练 习
解:
解:
解:
解:
1. 点与直线位置关系
存在点到直线的最短距离
2. 直线与直线位置关系
在同一平面上的直线之间,有相交、平行、重合三种位置关系,那么这三种位置关系反映在直线方程关系上如何呢?
设直角坐标系上两条直线的方程分别为:
结论:
结论:直线l1与 l2的交点个数与方程组(*)解的个数相同,即直线l1与 l2的交点情况等价于方程组(*)解的情况.
(1) 两直线的交点
(2)两直线的位置关系
方程组(*)有唯一解
即直线l1与 l2相交于一点,其交点坐标是
设直角坐标系上两条直线的方程分别为:
方程组(*)无解
即直线 l1// l2
方程组(*)有无穷多解
即直线l1与 l2重合
结论:D=0 即a1b2-a2b1=0 是直线l1与 l2平行或重合的必要条件.
特别地:
特别地
l1到 l2的角—
3. 两直线夹角
(1) 两直线所成角
l2到l1的角
(2) 两直线夹角
l1与 l2夹角— 两直线相交时其中所成的锐角(或直角)
规定: 如果两条直线平行或重合时,它们的夹角为0
(3) 两直线夹角公式
设两条直线l1与l2的方程分别为:
(4) 两直线夹角正切公式
(1)
(2)
x
y
O
O
y
x
x
y
O
x
y
O
解:
练 习
解:
解:
解:
解:
