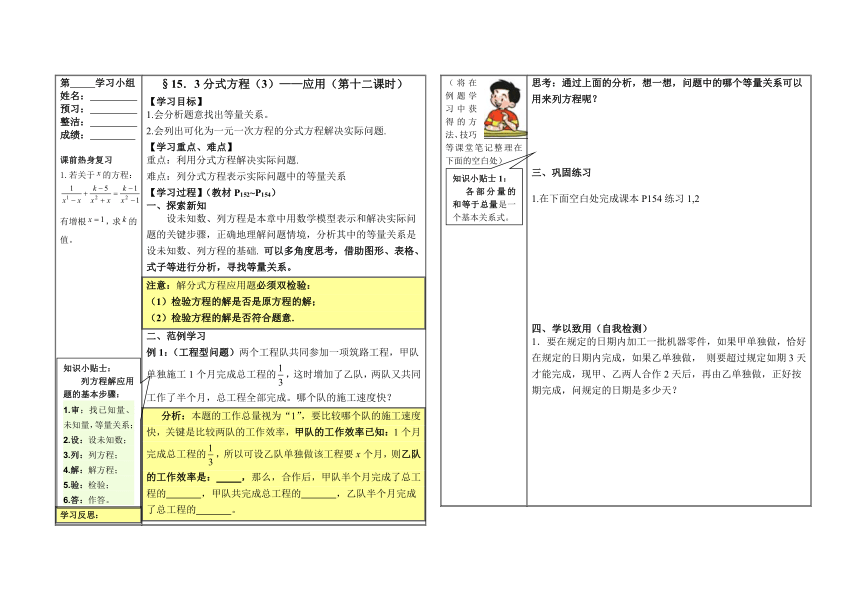
人教版八年级上册数学学案:15.3分式方程(3)——应用(表格式)
文档属性
| 名称 | 人教版八年级上册数学学案:15.3分式方程(3)——应用(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 53.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览

文档简介
第
学习小组
姓名:
预习:
整洁:
成绩:
课前热身复习
若关于的方程:有增根,求的
值。
学习反思:
(将在例题学习中获得的方法、技巧等课堂笔记整理在下面的空白处)
§15.3分式方程(3)——应用(第十二课时)
【学习目标】
会分析题意找出等量关系。
2.会列出可化为一元一次方程的分式方程解决实际问题.
【学习重点、难点】
重点:利用分式方程解决实际问题.
难点:列分式方程表示实际问题中的等量关系
【学习过程】(教材P152~P154)
一、探索新知
设未知数、列方程是本章中用数学模型表示和解决实际问题的关键步骤,正确地理解问题情境,分析其中的等量关系是设未知数、列方程的基础.
可以多角度思考,借助图形、表格、式子等进行分析,寻找等量关系。
注意:解分式方程应用题必须双检验:
检验方程的解是否是原方程的解;
检验方程的解是否符合题意.
范例学习
例1:(工程型问题)两个工程队共同参加一项筑路工程,甲队单独施工1个月完成总工程的,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
分析:本题的工作总量视为“1”,要比较哪个队的施工速度快,关键是比较两队的工作效率,甲队的工作效率已知:1个月完成总工程的,所以可设乙队单独做该工程要x个月,则乙队的工作效率是:
,那么,合作后,甲队半个月完成了总工程的
,甲队共完成总工程的
,乙队半个月完成了总工程的
。
思考:通过上面的分析,想一想,问题中的哪个等量关系可以用来列方程呢?
巩固练习
在下面空白处完成课本P154练习1,2
四、学以致用(自我检测)
1.要在规定的日期内加工一批机器零件,如果甲单独做,恰好在规定的日期内完成,如果乙单独做,
则要超过规定如期3天才能完成,现甲、乙两人合作2天后,再由乙单独做,正好按期完成,问规定的日期是多少天?
我的课堂笔记:
在此记录下
你的做题过程,对做错的题进行错因分析,改正相信
你会收获很
多。
本节反思
1.本节课你有哪些收获?(知识上,思想方法上)
2.课前你的疑难解决了吗?有没有新的问题?
2.一项工程要在限期内完成.如果第一组单独做,恰好按规定日期完成;如果第二组单独做,需要超过规定日期4天才能完成,如果两组合作3天后,剩下的工程由第二组单独做,正好在规定日期内完成,问规定日期是多少天?
3.甲、乙两个工程队共同完成一项工程,乙队先单独做1天后,再由两队合作2天就完成了全部工程,已知甲队单独完成工程所需的天数是乙队单独完成所需天数的,求甲、乙两队单独完成各需多少天?
4.某学校学生进行急行军训练,预计行60千米的路程在下午5时到达,后来由于把速度加快
,结果于下午4时到达,求原计划行军的速度。
5.甲、乙两地相距19千米,某人从甲地去乙地,先步行7千米,然后改骑自行车,共用了2小时到达乙地,已知这个人骑自行车的速度是步行速度的4倍,求步行的速度和骑自行车的速度.
6.
学校要举行跳绳比赛,同学们都积极练习.甲同学跳180个所用的时间,乙同学可以跳240个;又已知甲每分钟比乙少跳5个,求每人每分钟各跳多少个.
学习小组
姓名:
预习:
整洁:
成绩:
课前热身复习
若关于的方程:有增根,求的
值。
学习反思:
(将在例题学习中获得的方法、技巧等课堂笔记整理在下面的空白处)
§15.3分式方程(3)——应用(第十二课时)
【学习目标】
会分析题意找出等量关系。
2.会列出可化为一元一次方程的分式方程解决实际问题.
【学习重点、难点】
重点:利用分式方程解决实际问题.
难点:列分式方程表示实际问题中的等量关系
【学习过程】(教材P152~P154)
一、探索新知
设未知数、列方程是本章中用数学模型表示和解决实际问题的关键步骤,正确地理解问题情境,分析其中的等量关系是设未知数、列方程的基础.
可以多角度思考,借助图形、表格、式子等进行分析,寻找等量关系。
注意:解分式方程应用题必须双检验:
检验方程的解是否是原方程的解;
检验方程的解是否符合题意.
范例学习
例1:(工程型问题)两个工程队共同参加一项筑路工程,甲队单独施工1个月完成总工程的,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
分析:本题的工作总量视为“1”,要比较哪个队的施工速度快,关键是比较两队的工作效率,甲队的工作效率已知:1个月完成总工程的,所以可设乙队单独做该工程要x个月,则乙队的工作效率是:
,那么,合作后,甲队半个月完成了总工程的
,甲队共完成总工程的
,乙队半个月完成了总工程的
。
思考:通过上面的分析,想一想,问题中的哪个等量关系可以用来列方程呢?
巩固练习
在下面空白处完成课本P154练习1,2
四、学以致用(自我检测)
1.要在规定的日期内加工一批机器零件,如果甲单独做,恰好在规定的日期内完成,如果乙单独做,
则要超过规定如期3天才能完成,现甲、乙两人合作2天后,再由乙单独做,正好按期完成,问规定的日期是多少天?
我的课堂笔记:
在此记录下
你的做题过程,对做错的题进行错因分析,改正相信
你会收获很
多。
本节反思
1.本节课你有哪些收获?(知识上,思想方法上)
2.课前你的疑难解决了吗?有没有新的问题?
2.一项工程要在限期内完成.如果第一组单独做,恰好按规定日期完成;如果第二组单独做,需要超过规定日期4天才能完成,如果两组合作3天后,剩下的工程由第二组单独做,正好在规定日期内完成,问规定日期是多少天?
3.甲、乙两个工程队共同完成一项工程,乙队先单独做1天后,再由两队合作2天就完成了全部工程,已知甲队单独完成工程所需的天数是乙队单独完成所需天数的,求甲、乙两队单独完成各需多少天?
4.某学校学生进行急行军训练,预计行60千米的路程在下午5时到达,后来由于把速度加快
,结果于下午4时到达,求原计划行军的速度。
5.甲、乙两地相距19千米,某人从甲地去乙地,先步行7千米,然后改骑自行车,共用了2小时到达乙地,已知这个人骑自行车的速度是步行速度的4倍,求步行的速度和骑自行车的速度.
6.
学校要举行跳绳比赛,同学们都积极练习.甲同学跳180个所用的时间,乙同学可以跳240个;又已知甲每分钟比乙少跳5个,求每人每分钟各跳多少个.
