沪教版(上海)数学高一上册-3.4 函数的最大值、最小值 课件(15张PPT)
文档属性
| 名称 | 沪教版(上海)数学高一上册-3.4 函数的最大值、最小值 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 199.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 21:21:03 | ||
图片预览


文档简介
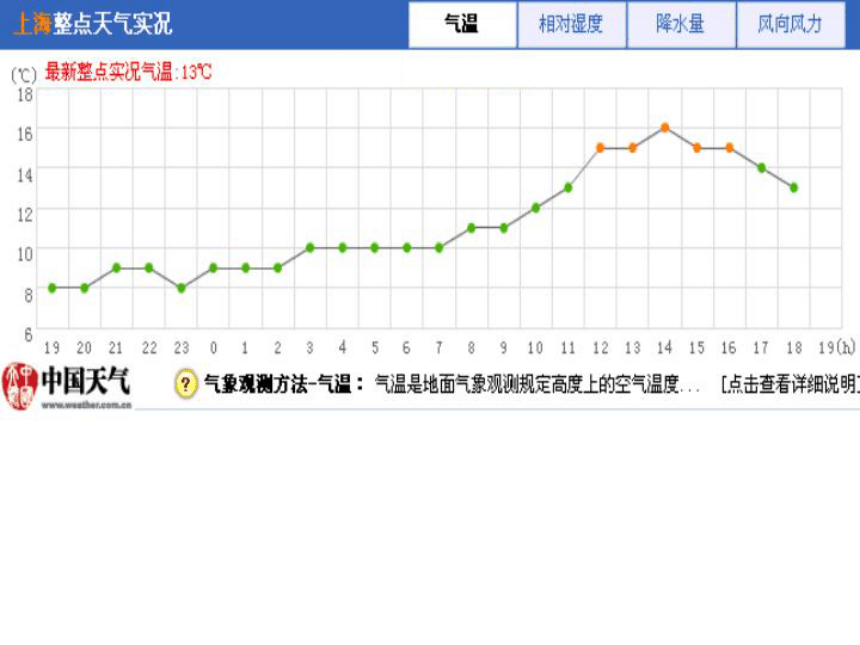
课题:函数的最大值、最小值
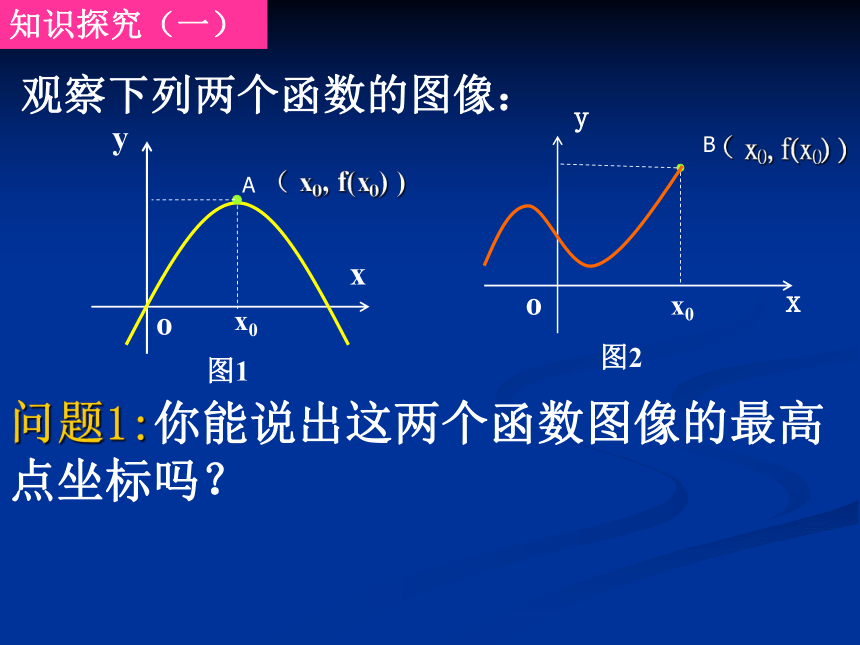
问题1:你能说出这两个函数图像的最高点坐标吗?
y
x
o
x0
图2
B
图1
o
x0
x
y
A
( x0, f(x0) )
知识探究(一)
观察下列两个函数的图像:
( x0, f(x0) )
y
x
o
x0
图2
B
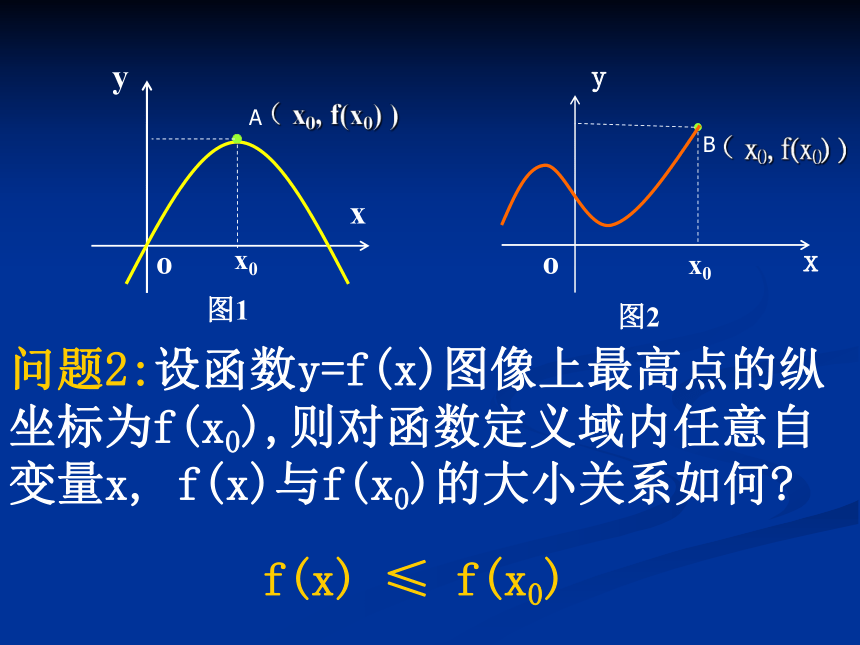
问题2:设函数y=f(x)图像上最高点的纵坐标为f(x0),则对函数定义域内任意自变量x, f(x)与f(x0)的大小关系如何?
图1
o
x0
x
y
A
( x0, f(x0) )
( x0, f(x0) )
f(x) ≤ f(x0)
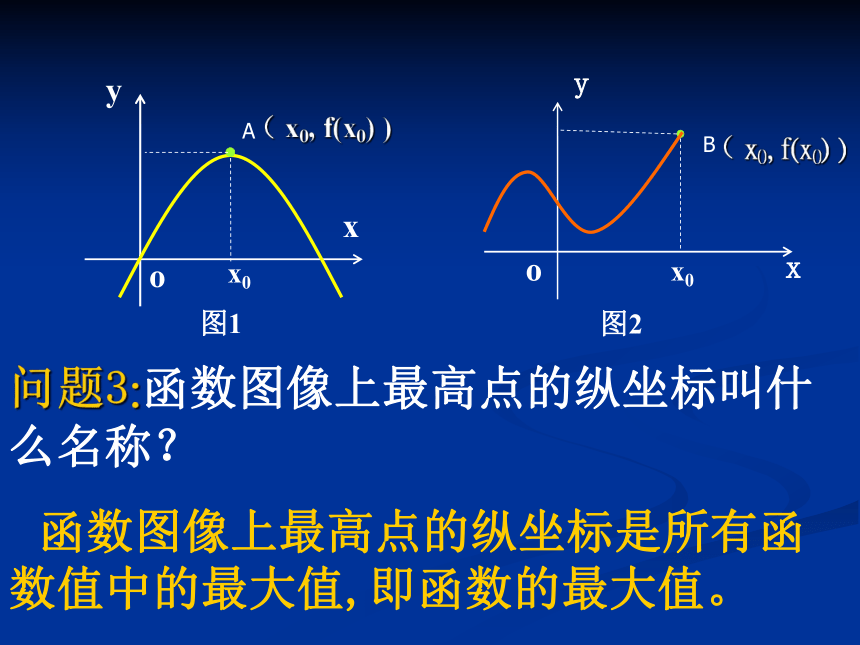
问题3:函数图像上最高点的纵坐标叫什么名称?
y
x
o
x0
图2
B
图1
o
x0
x
y
A
( x0, f(x0) )
( x0, f(x0) )
函数图像上最高点的纵坐标是所有函数值中的最大值,即函数的最大值。
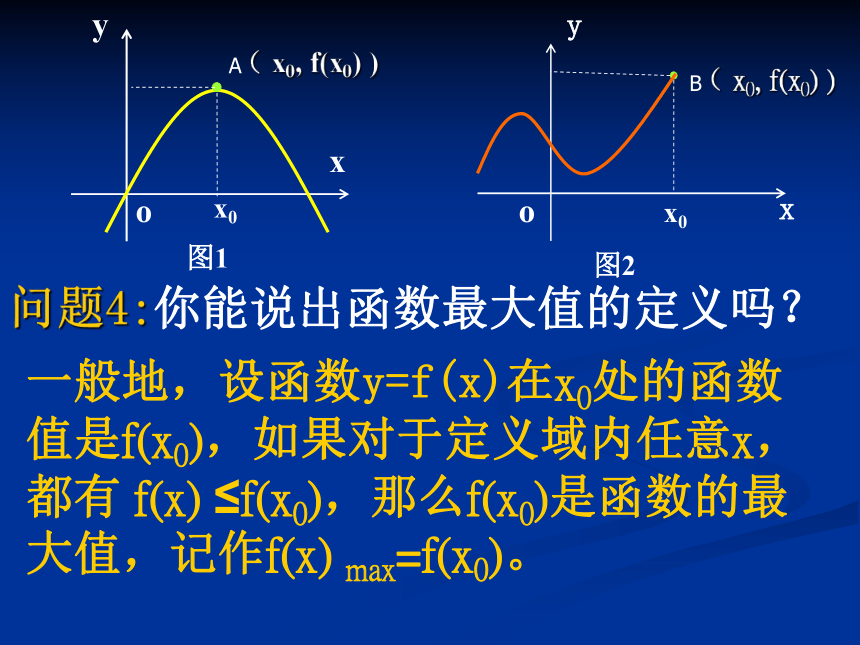
问题4:你能说出函数最大值的定义吗?
y
x
o
x0
图2
B
图1
o
x0
x
y
A
( x0, f(x0) )
( x0, f(x0) )
一般地,设函数y=f(x)在x0处的函数值是f(x0),如果对于定义域内任意x,都有 f(x) ≤f(x0),那么f(x0)是函数的最大值,记作f(x) max=f(x0)。
问题6:函数 有最大
值吗?为什么?点(-1,3)是不是最高点?由此你发现了什么值得注意的地方?
研究函数的最大值,要坚持定义域优先的原则;函数图像有最高点时,这个函数才存在最大值,最高点必须是函数图像上的点。
问题5:设函数f(x)=1-x2,则f(x) ≤2
成立吗? f(x)的最大值是2吗?为什么?
图3
y
o
x0
x
知识探究(二)
观察下列两个函数的图像:
x
y
o
x0
图4
问题1:这两个函数图像各有一个最低点,函数图像上最低点的纵坐标叫什么名称?
函数图像最低点的纵坐标即为函数最小值。
A( x0, f(x0) )
B( x0, f(x0) )
y
x
y
o
x0
图4
问题2:仿照函数最大值的定义,你能定义函数的最小值?
图3
o
x0
x
A( x0, f(x0) )
B( x0, f(x0) )
一般地,设函数y=f(x)在x0处的函数值是f(x0),如果对于定义域内任意x,都有 f(x) f(x0),那么f(x0)是函数的最小值,记作f(x)min=f(x0)。
≥
知识探究(三)
问题1:如果在函数 定义域内存在x1和x2,
对定义域内任意x都有
成立,由此你能得到什么结论?
问题2:如图函数 有最大值、最小值吗?对应的x为何值?
Y
X
0
-3
1
4
8
7
函数的最大值、最小值:
图像
定义
函数的最大(小)值是函数图像上最高(低)点的纵坐标
一般地,设函数y=f(x)在x0处的函数值是f(x0),如果对于定义域内任意x,都有 f(x) ≤f(x0),那么f(x0)是函数的最大值,记作f(x) max=f(x0)。
一般地,设函数y=f(x)在x0处的函数值是f(x0),如果对于定义域内任意x,都有 f(x) ≥f(x0),那么f(x0)是函数的最小值,记作f(x)min=f(x0)。
怎么求函数的最大值、最小值呢?
例 题:求二次函数y=x2+2x+8的最大值、最小值
变式1:求二次函数y=-x2+2x+8的最大值、
最小值
变式2:求二次函数y=-x2+2x+8在区间
的最大值、最小值
变式3:求二次函数y=-x2+2x+8在区间
的最大值、最小值
知识探究(四)
课堂小结:
1、一种思想:数形结合思想
2、两个定义:函数的最大值和最小值
3、三种方法:求函数的最大和最小值的重要方法
①配方法
②利用函数的单调性
③图像法
课后作业:
1.练习册P33 A组9、10、11
2.动物园要建造一面靠墙的2间面积相同的矩形熊猫居室。如果可供建造围墙的材料总长是30米,那么宽为多少米时才能使所建造的熊猫居室面积最大?熊猫居室的最大面积是多少平方米?
3.求二次函数y=-x2+2ax+8在区间
的最大值、最小值。
谢 谢
问题1:你能说出这两个函数图像的最高点坐标吗?
y
x
o
x0
图2
B
图1
o
x0
x
y
A
( x0, f(x0) )
知识探究(一)
观察下列两个函数的图像:
( x0, f(x0) )
y
x
o
x0
图2
B
问题2:设函数y=f(x)图像上最高点的纵坐标为f(x0),则对函数定义域内任意自变量x, f(x)与f(x0)的大小关系如何?
图1
o
x0
x
y
A
( x0, f(x0) )
( x0, f(x0) )
f(x) ≤ f(x0)
问题3:函数图像上最高点的纵坐标叫什么名称?
y
x
o
x0
图2
B
图1
o
x0
x
y
A
( x0, f(x0) )
( x0, f(x0) )
函数图像上最高点的纵坐标是所有函数值中的最大值,即函数的最大值。
问题4:你能说出函数最大值的定义吗?
y
x
o
x0
图2
B
图1
o
x0
x
y
A
( x0, f(x0) )
( x0, f(x0) )
一般地,设函数y=f(x)在x0处的函数值是f(x0),如果对于定义域内任意x,都有 f(x) ≤f(x0),那么f(x0)是函数的最大值,记作f(x) max=f(x0)。
问题6:函数 有最大
值吗?为什么?点(-1,3)是不是最高点?由此你发现了什么值得注意的地方?
研究函数的最大值,要坚持定义域优先的原则;函数图像有最高点时,这个函数才存在最大值,最高点必须是函数图像上的点。
问题5:设函数f(x)=1-x2,则f(x) ≤2
成立吗? f(x)的最大值是2吗?为什么?
图3
y
o
x0
x
知识探究(二)
观察下列两个函数的图像:
x
y
o
x0
图4
问题1:这两个函数图像各有一个最低点,函数图像上最低点的纵坐标叫什么名称?
函数图像最低点的纵坐标即为函数最小值。
A( x0, f(x0) )
B( x0, f(x0) )
y
x
y
o
x0
图4
问题2:仿照函数最大值的定义,你能定义函数的最小值?
图3
o
x0
x
A( x0, f(x0) )
B( x0, f(x0) )
一般地,设函数y=f(x)在x0处的函数值是f(x0),如果对于定义域内任意x,都有 f(x) f(x0),那么f(x0)是函数的最小值,记作f(x)min=f(x0)。
≥
知识探究(三)
问题1:如果在函数 定义域内存在x1和x2,
对定义域内任意x都有
成立,由此你能得到什么结论?
问题2:如图函数 有最大值、最小值吗?对应的x为何值?
Y
X
0
-3
1
4
8
7
函数的最大值、最小值:
图像
定义
函数的最大(小)值是函数图像上最高(低)点的纵坐标
一般地,设函数y=f(x)在x0处的函数值是f(x0),如果对于定义域内任意x,都有 f(x) ≤f(x0),那么f(x0)是函数的最大值,记作f(x) max=f(x0)。
一般地,设函数y=f(x)在x0处的函数值是f(x0),如果对于定义域内任意x,都有 f(x) ≥f(x0),那么f(x0)是函数的最小值,记作f(x)min=f(x0)。
怎么求函数的最大值、最小值呢?
例 题:求二次函数y=x2+2x+8的最大值、最小值
变式1:求二次函数y=-x2+2x+8的最大值、
最小值
变式2:求二次函数y=-x2+2x+8在区间
的最大值、最小值
变式3:求二次函数y=-x2+2x+8在区间
的最大值、最小值
知识探究(四)
课堂小结:
1、一种思想:数形结合思想
2、两个定义:函数的最大值和最小值
3、三种方法:求函数的最大和最小值的重要方法
①配方法
②利用函数的单调性
③图像法
课后作业:
1.练习册P33 A组9、10、11
2.动物园要建造一面靠墙的2间面积相同的矩形熊猫居室。如果可供建造围墙的材料总长是30米,那么宽为多少米时才能使所建造的熊猫居室面积最大?熊猫居室的最大面积是多少平方米?
3.求二次函数y=-x2+2ax+8在区间
的最大值、最小值。
谢 谢
