沪教版(上海)数学高一上册-4.1 函数图像变换 课件(26张PPT)
文档属性
| 名称 | 沪教版(上海)数学高一上册-4.1 函数图像变换 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 771.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览




文档简介
函数图像变换
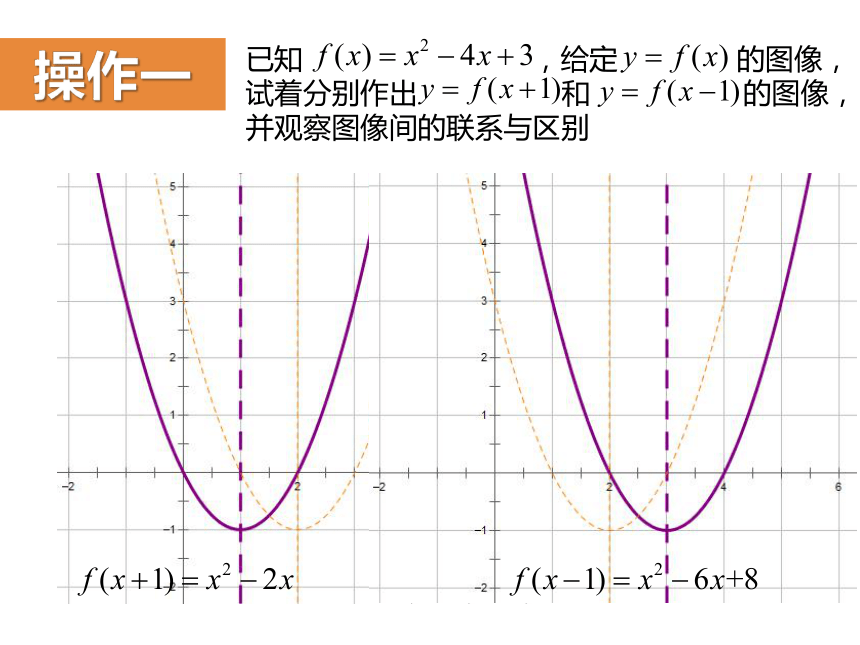
已知 ,给定 的图像,
试着分别作出 和 的图像,
并观察图像间的联系与区别
操作一
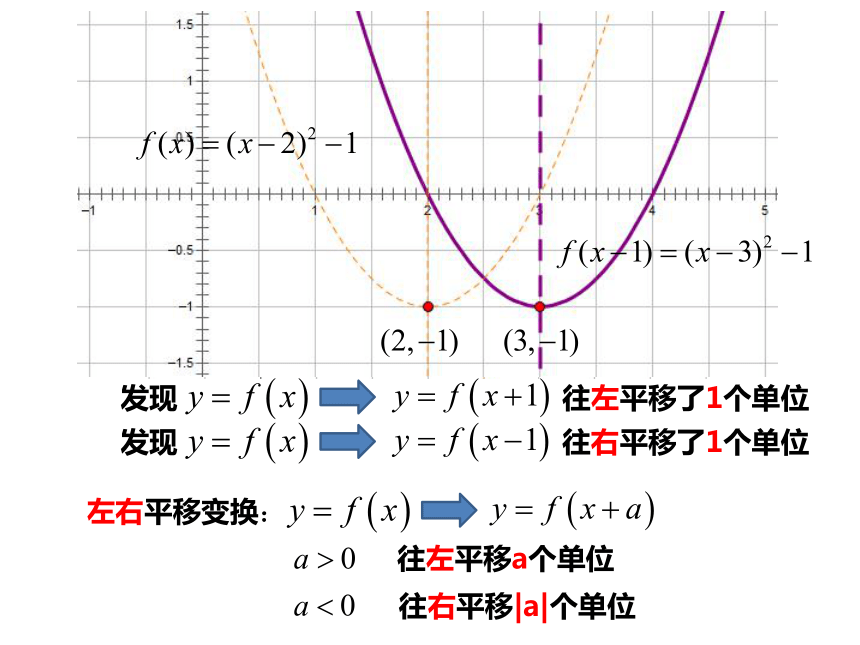
发现 往左平移了1个单位
左右平移变换:
往左平移a个单位
往右平移|a|个单位
发现 往右平移了1个单位
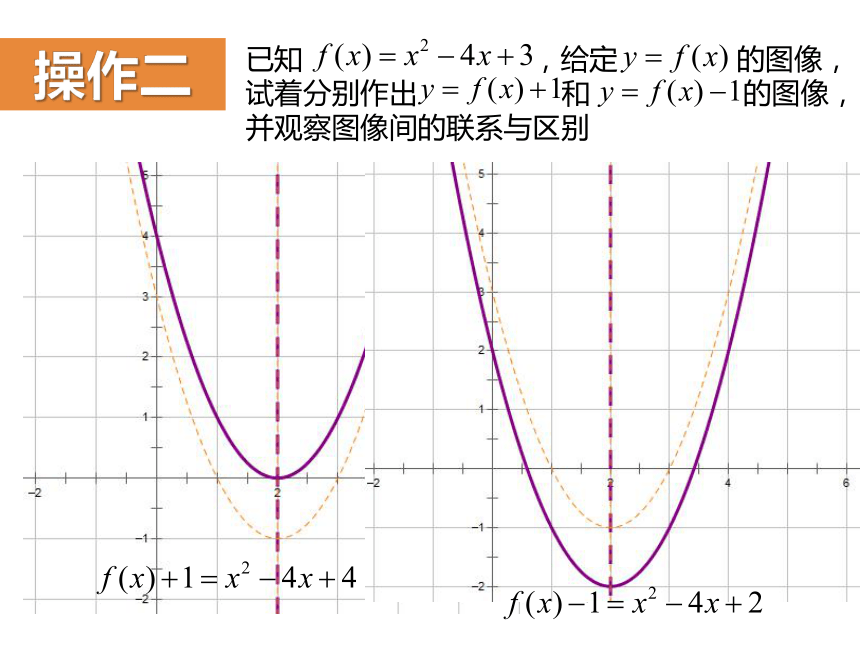
操作二
已知 ,给定 的图像,
试着分别作出 和 的图像,
并观察图像间的联系与区别
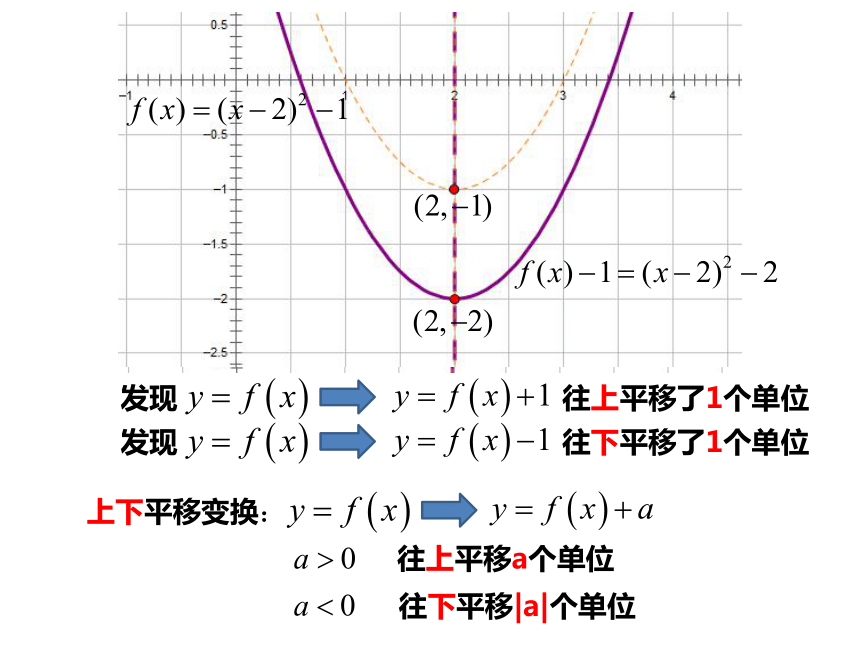
发现 往上平移了1个单位
上下平移变换:
往上平移a个单位
往下平移|a|个单位
发现 往下平移了1个单位
上下平移变换:
左右平移变换:
平移变换
总结:解析式中,左加右减,上加下减
往左平移a个单位
往右平移|a|个单位
往上平移a个单位
往下平移|a|个单位
学以致用
例题1:
(1) 可以由 通过怎样的图像变换得到?
(2) 可以由 通过怎样的图像变换得到?
学以致用
例题1:
(3) 可以由 通过怎样的图像变换得到?
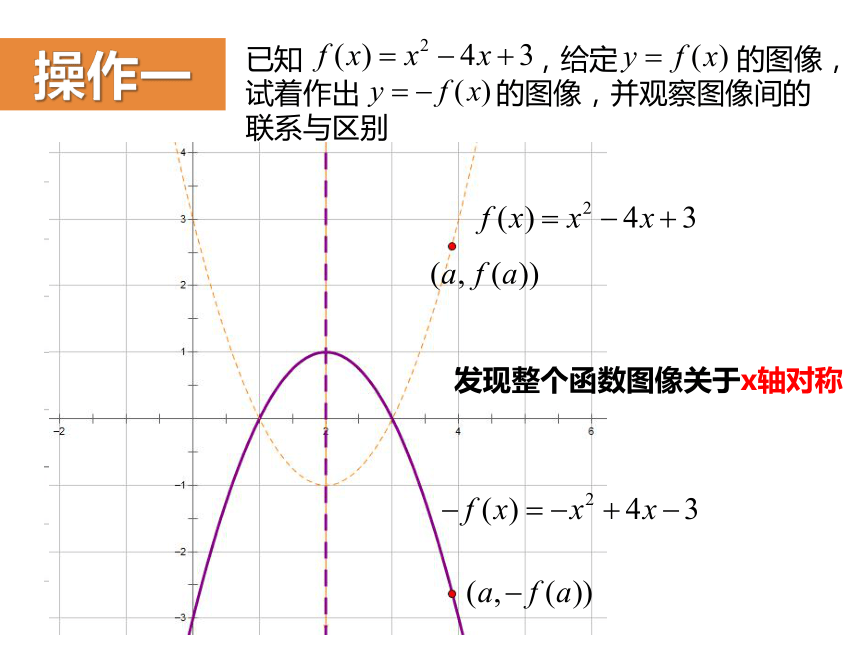
已知 ,给定 的图像,
试着作出 的图像,并观察图像间的
联系与区别
操作一
发现整个函数图像关于x轴对称
已知 ,给定 的图像,
试着作出 的图像,并观察图像间的
联系与区别
操作二
发现整个函数图像关于y轴对称
已知 ,给定 的图像,
试着作出 的图像,并观察图像间的
联系与区别
操作三
发现整个函数图像关于原点对称
先关于y轴对称,再关于x轴对称
所以图像关于原点对称
关于x轴对称:
关于y轴对称:
对称变换
关于原点对称:
已知 ,给定 的图像,
试着作出 的图像,并观察图像间的
联系与区别
操作一
(1)保留x轴上方及x轴上的点
(2)将x轴下方部分关于x轴
对称向上翻折
已知 ,给定 的图像,
试着作出 的图像,并观察图像间的
联系与区别
操作二
(1)画出y轴右边及y轴上的点
(2)再将y轴右侧部分关于y轴
对称向左翻折
翻折变换
(1)保留x轴上方及x轴上部分
(2)将x轴下方部分关于x轴
对称向上翻折
(1)画出y轴右边及y轴上的点
(2)再将y轴右侧部分关于y轴
对称向左翻折
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
图像关于y轴对称
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
图像关于x轴对称
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
图像关于原点对称
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
学以致用
例3:
1、关于 的方程 有三个不相等的实数根,求实数 的值。
学以致用
例3:
2、讨论关于 的方程 的根的个数。
学以致用
例3:
3、设定义域为R的函数 ,若关于 的方程
有3个
不同的实数解, ,则 的值等于( )
A、5 B、 C、13 D、
总结
上下平移变换:
左右平移变换:
往左平移a个单位
往右平移|a|个单位
往上平移a个单位
往下平移|a|个单位
左加右减,上加下减
关于x轴对称:
关于y轴对称:
关于原点对称:
关于x轴翻折:
关于y轴翻折:
已知 ,给定 的图像,
试着分别作出 和 的图像,
并观察图像间的联系与区别
操作一
发现 往左平移了1个单位
左右平移变换:
往左平移a个单位
往右平移|a|个单位
发现 往右平移了1个单位
操作二
已知 ,给定 的图像,
试着分别作出 和 的图像,
并观察图像间的联系与区别
发现 往上平移了1个单位
上下平移变换:
往上平移a个单位
往下平移|a|个单位
发现 往下平移了1个单位
上下平移变换:
左右平移变换:
平移变换
总结:解析式中,左加右减,上加下减
往左平移a个单位
往右平移|a|个单位
往上平移a个单位
往下平移|a|个单位
学以致用
例题1:
(1) 可以由 通过怎样的图像变换得到?
(2) 可以由 通过怎样的图像变换得到?
学以致用
例题1:
(3) 可以由 通过怎样的图像变换得到?
已知 ,给定 的图像,
试着作出 的图像,并观察图像间的
联系与区别
操作一
发现整个函数图像关于x轴对称
已知 ,给定 的图像,
试着作出 的图像,并观察图像间的
联系与区别
操作二
发现整个函数图像关于y轴对称
已知 ,给定 的图像,
试着作出 的图像,并观察图像间的
联系与区别
操作三
发现整个函数图像关于原点对称
先关于y轴对称,再关于x轴对称
所以图像关于原点对称
关于x轴对称:
关于y轴对称:
对称变换
关于原点对称:
已知 ,给定 的图像,
试着作出 的图像,并观察图像间的
联系与区别
操作一
(1)保留x轴上方及x轴上的点
(2)将x轴下方部分关于x轴
对称向上翻折
已知 ,给定 的图像,
试着作出 的图像,并观察图像间的
联系与区别
操作二
(1)画出y轴右边及y轴上的点
(2)再将y轴右侧部分关于y轴
对称向左翻折
翻折变换
(1)保留x轴上方及x轴上部分
(2)将x轴下方部分关于x轴
对称向上翻折
(1)画出y轴右边及y轴上的点
(2)再将y轴右侧部分关于y轴
对称向左翻折
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
图像关于y轴对称
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
图像关于x轴对称
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
图像关于原点对称
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
学以致用
例2:已知 的函数图像如图,写出下列函数图像的解析式。
学以致用
例3:
1、关于 的方程 有三个不相等的实数根,求实数 的值。
学以致用
例3:
2、讨论关于 的方程 的根的个数。
学以致用
例3:
3、设定义域为R的函数 ,若关于 的方程
有3个
不同的实数解, ,则 的值等于( )
A、5 B、 C、13 D、
总结
上下平移变换:
左右平移变换:
往左平移a个单位
往右平移|a|个单位
往上平移a个单位
往下平移|a|个单位
左加右减,上加下减
关于x轴对称:
关于y轴对称:
关于原点对称:
关于x轴翻折:
关于y轴翻折:
