沪教版(上海)数学高一上册-4.1 幂函数的图象与性质(一) 课件(15张PPT)
文档属性
| 名称 | 沪教版(上海)数学高一上册-4.1 幂函数的图象与性质(一) 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 175.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 21:24:24 | ||
图片预览




文档简介
幂函数
汨罗市一中高一数学组 文怀
问题引入:
1.如果张红购买了每千克1元的水果x千克,她需要付的钱数
为y(元),试将y表示成x的函数.
2.如果正方形的边长为x,面积为y,试将y表示成x的函数.
3.如果立方体的棱长为x,体积为y,试将y表示成x的函数.
4.如果一个正方形场地的面积为x,正方形的边长为y,试将
y表示成x的函数.
5.如果某人x秒内骑车行进了1km,他骑车的平均速度为ykm/s,试将y表示成x的函数.
探究(一):幂函数的概念
思考:这些函数有什么共同的结构特征?
探究(一):幂函数的概念
一.幂函数的概念
一般的,函数 叫做
幂函数,其中x是自变量, 是常数。
1.判断下列函数是否为幂函数.
(1) y=4x
(3) y= -x2
(5) y=2x2
(6) y=x3+x
练习1:
)
2
(
2.已知幂函数f(x)的图象过点 ,则f(4)的值是______________.
)
4
(
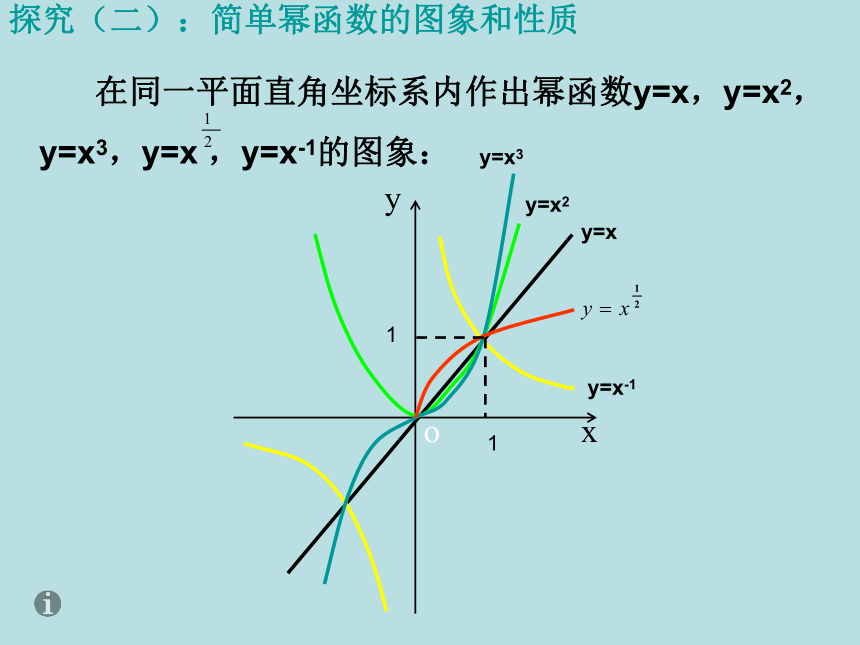
探究(二):简单幂函数的图象和性质
在同一平面直角坐标系内作出幂函数y=x,y=x2,
y=x3,y=x ,y=x-1的图象:
x
y
o
y=x
y=x2
y=x-1
y=x3
1
1
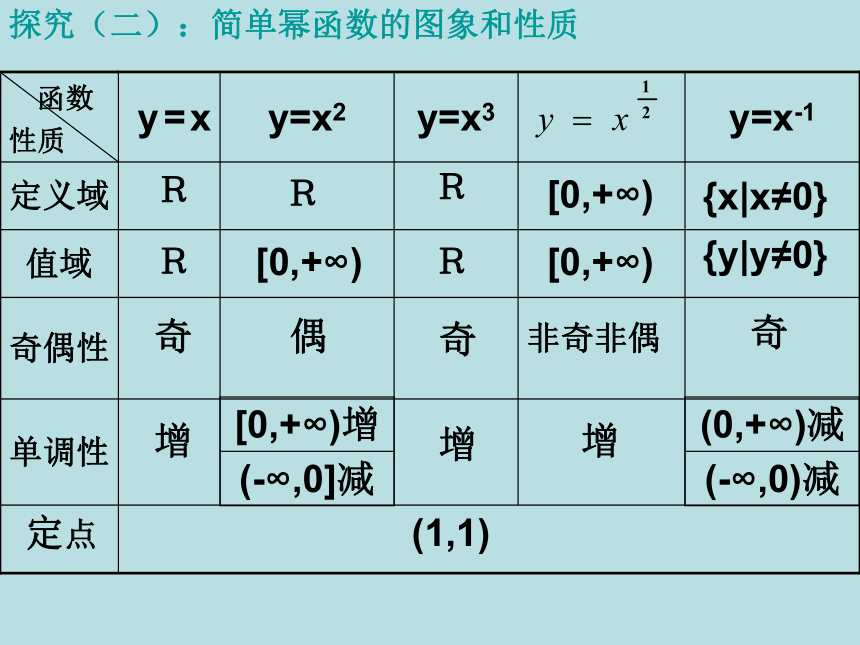
函数
性质
y=x
y=x2
y=x3
y=x-1
定义域
值域
奇偶性
单调性
R
R
奇
奇
奇
增
增
增
R
[0,+∞)
[0,+∞)
[0,+∞)
偶
(-∞,0]减
[0,+∞)增
R
R
非奇非偶
{x|x≠0}
{y|y≠0}
(-∞,0)减
(0,+∞)减
(1,1)
定点
探究(二):简单幂函数的图象和性质
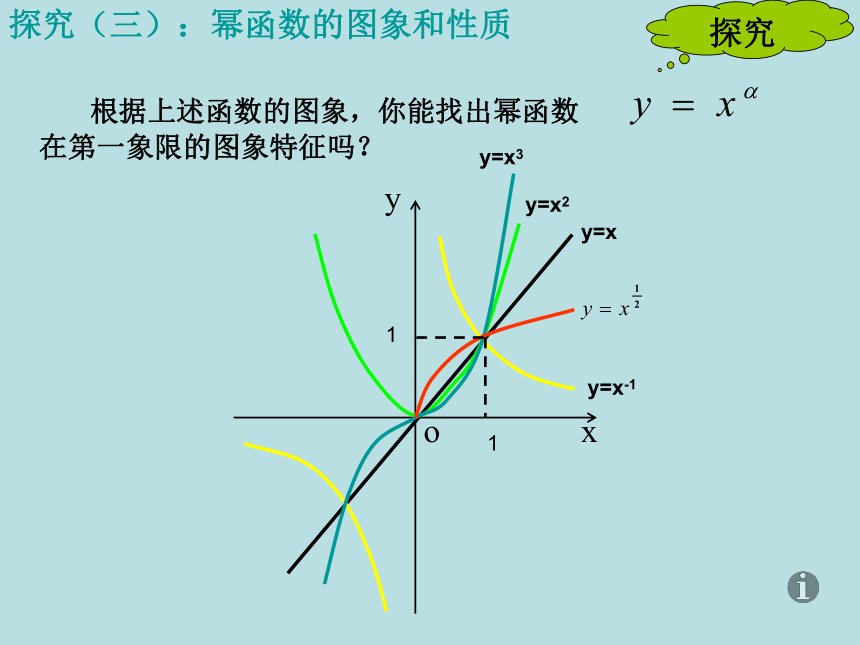
探究(三):幂函数的图象和性质
根据上述函数的图象,你能找出幂函数 在第一象限的图象特征吗?
探究
x
y
o
y=x
y=x2
y=x-1
y=x3
1
1
x
y
o
=1
>1
0< <1
<0
探究(三):幂函数的图象和性质
幂函数 在(0,+∞)的性质:
1
1
1.图象过定点(1,1)
2. 函数在 上是单调增函数。
[0,+∞)
3. 函数在 上是单调减函数。
(0,+∞)
例1:
讨论函数 的定义域、值域、奇偶性、
单调性,并画出图象的示意图.
如何作幂函数的图象?
思考
一、作幂函数的大致图象的方法:
描点法、利用性质作图法
归纳
二、利用性质作图的步骤:
1.先作函数在第一象限内的图象,
2.利用函数的定义域和奇偶性作出函数在其他
象限内的图象。(奇,偶,非奇非偶函数)
1.作出函数 的大致图象。
练习3:
2.比较下列各组数的大小。
3
2
3
1
3
1
)
6
(
)
3
2
(
)
2
(
7
.
1
1.5
)
1
(
3
2
-
-
-
-
和
和
p
比较幂值的大小的常用方法:
归纳
1.单调性法
2.中间量法
课堂小结
内容: 幂函数的概念、图象和性质;
重点: 幂函数的图象、性质及简单应用;
关键: 幂函数指数 的变化对函数图
象性质的影响;
思想方法: 数形结合思想、由特殊到一般的
思想方法
已知函数 是幂函数,且
在 上是减函数,求满足条件的实数m的值。
思考
1.下列函数 ,其
中定义域为R的函数有( )个,奇函数有( )个。
课后练习:
3.请将 按由小到大的
顺序排列:_________________________
2
2
2.若幂函数 的图象在 时位于直线y=x
的下方,则实数 的取值范围是( )
A B C D
B
再见!
汨罗市一中高一数学组 文怀
问题引入:
1.如果张红购买了每千克1元的水果x千克,她需要付的钱数
为y(元),试将y表示成x的函数.
2.如果正方形的边长为x,面积为y,试将y表示成x的函数.
3.如果立方体的棱长为x,体积为y,试将y表示成x的函数.
4.如果一个正方形场地的面积为x,正方形的边长为y,试将
y表示成x的函数.
5.如果某人x秒内骑车行进了1km,他骑车的平均速度为ykm/s,试将y表示成x的函数.
探究(一):幂函数的概念
思考:这些函数有什么共同的结构特征?
探究(一):幂函数的概念
一.幂函数的概念
一般的,函数 叫做
幂函数,其中x是自变量, 是常数。
1.判断下列函数是否为幂函数.
(1) y=4x
(3) y= -x2
(5) y=2x2
(6) y=x3+x
练习1:
)
2
(
2.已知幂函数f(x)的图象过点 ,则f(4)的值是______________.
)
4
(
探究(二):简单幂函数的图象和性质
在同一平面直角坐标系内作出幂函数y=x,y=x2,
y=x3,y=x ,y=x-1的图象:
x
y
o
y=x
y=x2
y=x-1
y=x3
1
1
函数
性质
y=x
y=x2
y=x3
y=x-1
定义域
值域
奇偶性
单调性
R
R
奇
奇
奇
增
增
增
R
[0,+∞)
[0,+∞)
[0,+∞)
偶
(-∞,0]减
[0,+∞)增
R
R
非奇非偶
{x|x≠0}
{y|y≠0}
(-∞,0)减
(0,+∞)减
(1,1)
定点
探究(二):简单幂函数的图象和性质
探究(三):幂函数的图象和性质
根据上述函数的图象,你能找出幂函数 在第一象限的图象特征吗?
探究
x
y
o
y=x
y=x2
y=x-1
y=x3
1
1
x
y
o
=1
>1
0< <1
<0
探究(三):幂函数的图象和性质
幂函数 在(0,+∞)的性质:
1
1
1.图象过定点(1,1)
2. 函数在 上是单调增函数。
[0,+∞)
3. 函数在 上是单调减函数。
(0,+∞)
例1:
讨论函数 的定义域、值域、奇偶性、
单调性,并画出图象的示意图.
如何作幂函数的图象?
思考
一、作幂函数的大致图象的方法:
描点法、利用性质作图法
归纳
二、利用性质作图的步骤:
1.先作函数在第一象限内的图象,
2.利用函数的定义域和奇偶性作出函数在其他
象限内的图象。(奇,偶,非奇非偶函数)
1.作出函数 的大致图象。
练习3:
2.比较下列各组数的大小。
3
2
3
1
3
1
)
6
(
)
3
2
(
)
2
(
7
.
1
1.5
)
1
(
3
2
-
-
-
-
和
和
p
比较幂值的大小的常用方法:
归纳
1.单调性法
2.中间量法
课堂小结
内容: 幂函数的概念、图象和性质;
重点: 幂函数的图象、性质及简单应用;
关键: 幂函数指数 的变化对函数图
象性质的影响;
思想方法: 数形结合思想、由特殊到一般的
思想方法
已知函数 是幂函数,且
在 上是减函数,求满足条件的实数m的值。
思考
1.下列函数 ,其
中定义域为R的函数有( )个,奇函数有( )个。
课后练习:
3.请将 按由小到大的
顺序排列:_________________________
2
2
2.若幂函数 的图象在 时位于直线y=x
的下方,则实数 的取值范围是( )
A B C D
B
再见!
