沪教版(上海)数学高一上册-4.1 幂函数课件(28张PPT)
文档属性
| 名称 | 沪教版(上海)数学高一上册-4.1 幂函数课件(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 362.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 21:26:54 | ||
图片预览








文档简介
幂函数
问题引入:
1.如果小李购买了每千克 1 元的蔬菜 千克,那么他需要支付的钱数 P= 元。
2. 若正方形的边长为 ,则正方形的面积为 S= 。
3. 若立方体的的边长为 ,则立方体的体积为 V= 。
4. 若一个正方形场地的面积为 ,正方形的边长为 。
5. 若某人 秒内骑车行进 1 千米,他骑车的平均速度为 。
思考:上面的这些函数有什么共同的特征?
(1)都是函数;
(2)指数为常数;
(3)均是以自变量为底的幂。
幂函数的定义:
1.一般地,函数 ( 为常数, )叫做幂函数(power function)。
2.A function of the form , where is a constant, is called a power function.
注意:
1.幂函数 中 前面的系数为 1,且只有一项;
2.定义域不固定,与 的取值有关。
例题:
例1.判断下列函数哪些是幂函数:
(1) (2) (3) (4) (5)
例2.已知函数 是幂函数,求实数 的值。
探究:
画出下列函数的图像,指出它们的定义域、值域,并判断它们的奇偶性和单调性。
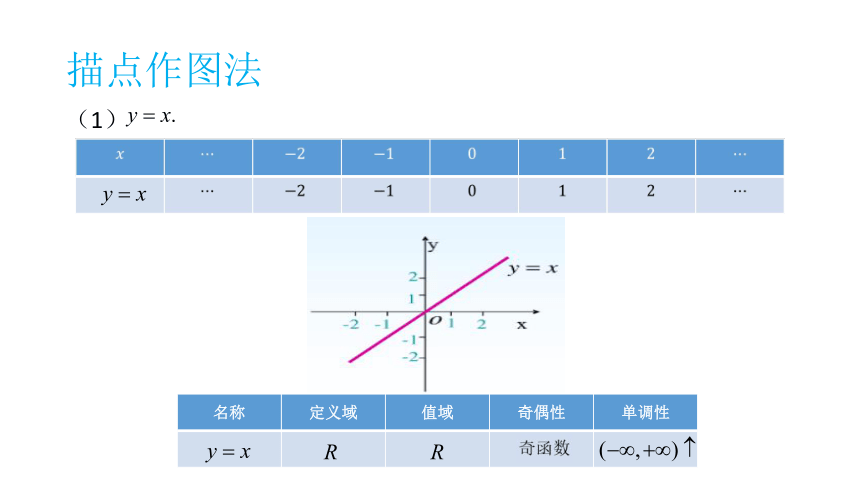
(1)
描点作图法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
定义域
值域
奇偶性
单调性
(2)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
定义域
值域
奇偶性
单调性
(3)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
定义域
值域
奇偶性
单调性
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
定义域
值域
奇偶性
单调性
(4)
(5)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
定义域
值域
奇偶性
单调性
结论:
y
x
0
1
1
y=x
幂函数的性质:
(1)幂函数在第一象限内的图像:
(2)所有的幂函数恒过点(1,1),
且当 时,幂函数还过点(0,0);
(3)所有幂函数的图像都经过第一象限,不经过第四象限;
(4)当 时, 越大,幂函数在第一象限的图像越靠近 轴。
(5)当 为奇数时,幂函数为奇函数;
当 为偶数时,幂函数为偶函数;
(6)当 时,幂函数在第一象限内是递增的;
当 时,幂函数在第一象限内是递减的;
例题:
例3.下列说法正确的是( )
(A)幂函数的图像都经过点(0,0)和点(1,1);
(B)幂函数的图像不可能出现在第四象限;
(C)当 时,幂函数 的值随 的增大而增大;
(D)当 时,幂函数 的图像是一条直线。
例4. Arrange the following triples in ascending order without using a calculator.
(1)
(2)
(3)
练习1.求一个幂函数,使其过点 。
练习2.幂函数 的图像过点 ,求 的值。
课堂练习:
练习3.设 ,求 的取值范围。
练习4.如果函数 是幂函数,且在区间 上是减函数,求满足条件的实数 的值。
思考题:
当幂函数的表达式为 ( , 且 )时的定义域、值域、奇偶性和单调性是怎样的?
例5:求下列函数的定义域、值域、奇偶性和单调性。
(1) (2)
(3) (4)
(5)
Domains of Power Functions
Domain of the power function is:
● if is odd and ;
● if is odd and ;
● if is even and ;
● if is even and .
奇偶性:
函数 的奇偶性:
当 为奇数, 为偶数时,函数是偶函数;
当 为奇数, 为奇数时,函数是奇函数;
当 为偶数, 为奇数时,函数是非奇非偶函数。
Monotonicity of Power Functions
Monotonicity of the power function is:
●increasing if is odd and ; decreasing if is odd and is even
with ; both increasing and decreasing if ;
●increasing for and decreasing for if is even and ;
decreasing for and increasing for if is even and ;
●decreasing for either or if is odd and .
课堂小结:
幂函数的定义;
幂函数的一些性质;
幂函数的应用(判断两个实数的大小关系)。
作业:
课本第81页的第1、2、3题。
问题引入:
1.如果小李购买了每千克 1 元的蔬菜 千克,那么他需要支付的钱数 P= 元。
2. 若正方形的边长为 ,则正方形的面积为 S= 。
3. 若立方体的的边长为 ,则立方体的体积为 V= 。
4. 若一个正方形场地的面积为 ,正方形的边长为 。
5. 若某人 秒内骑车行进 1 千米,他骑车的平均速度为 。
思考:上面的这些函数有什么共同的特征?
(1)都是函数;
(2)指数为常数;
(3)均是以自变量为底的幂。
幂函数的定义:
1.一般地,函数 ( 为常数, )叫做幂函数(power function)。
2.A function of the form , where is a constant, is called a power function.
注意:
1.幂函数 中 前面的系数为 1,且只有一项;
2.定义域不固定,与 的取值有关。
例题:
例1.判断下列函数哪些是幂函数:
(1) (2) (3) (4) (5)
例2.已知函数 是幂函数,求实数 的值。
探究:
画出下列函数的图像,指出它们的定义域、值域,并判断它们的奇偶性和单调性。
(1)
描点作图法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
定义域
值域
奇偶性
单调性
(2)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
定义域
值域
奇偶性
单调性
(3)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
定义域
值域
奇偶性
单调性
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
定义域
值域
奇偶性
单调性
(4)
(5)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
定义域
值域
奇偶性
单调性
结论:
y
x
0
1
1
y=x
幂函数的性质:
(1)幂函数在第一象限内的图像:
(2)所有的幂函数恒过点(1,1),
且当 时,幂函数还过点(0,0);
(3)所有幂函数的图像都经过第一象限,不经过第四象限;
(4)当 时, 越大,幂函数在第一象限的图像越靠近 轴。
(5)当 为奇数时,幂函数为奇函数;
当 为偶数时,幂函数为偶函数;
(6)当 时,幂函数在第一象限内是递增的;
当 时,幂函数在第一象限内是递减的;
例题:
例3.下列说法正确的是( )
(A)幂函数的图像都经过点(0,0)和点(1,1);
(B)幂函数的图像不可能出现在第四象限;
(C)当 时,幂函数 的值随 的增大而增大;
(D)当 时,幂函数 的图像是一条直线。
例4. Arrange the following triples in ascending order without using a calculator.
(1)
(2)
(3)
练习1.求一个幂函数,使其过点 。
练习2.幂函数 的图像过点 ,求 的值。
课堂练习:
练习3.设 ,求 的取值范围。
练习4.如果函数 是幂函数,且在区间 上是减函数,求满足条件的实数 的值。
思考题:
当幂函数的表达式为 ( , 且 )时的定义域、值域、奇偶性和单调性是怎样的?
例5:求下列函数的定义域、值域、奇偶性和单调性。
(1) (2)
(3) (4)
(5)
Domains of Power Functions
Domain of the power function is:
● if is odd and ;
● if is odd and ;
● if is even and ;
● if is even and .
奇偶性:
函数 的奇偶性:
当 为奇数, 为偶数时,函数是偶函数;
当 为奇数, 为奇数时,函数是奇函数;
当 为偶数, 为奇数时,函数是非奇非偶函数。
Monotonicity of Power Functions
Monotonicity of the power function is:
●increasing if is odd and ; decreasing if is odd and is even
with ; both increasing and decreasing if ;
●increasing for and decreasing for if is even and ;
decreasing for and increasing for if is even and ;
●decreasing for either or if is odd and .
课堂小结:
幂函数的定义;
幂函数的一些性质;
幂函数的应用(判断两个实数的大小关系)。
作业:
课本第81页的第1、2、3题。
