沪教版(上海)数学高一上册-4.2 指数函数的图像与性质 课件 (1)(13张PPT)
文档属性
| 名称 | 沪教版(上海)数学高一上册-4.2 指数函数的图像与性质 课件 (1)(13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 117.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览




文档简介
指数函数的图像与性质
温故而知新
分数指数幂的运算性质
(1)正分数指数幂的意义:
(2)负分数指数幂与负整数指数幂的意义相仿:
(3)运算性质:(a,b>0,m,n R)
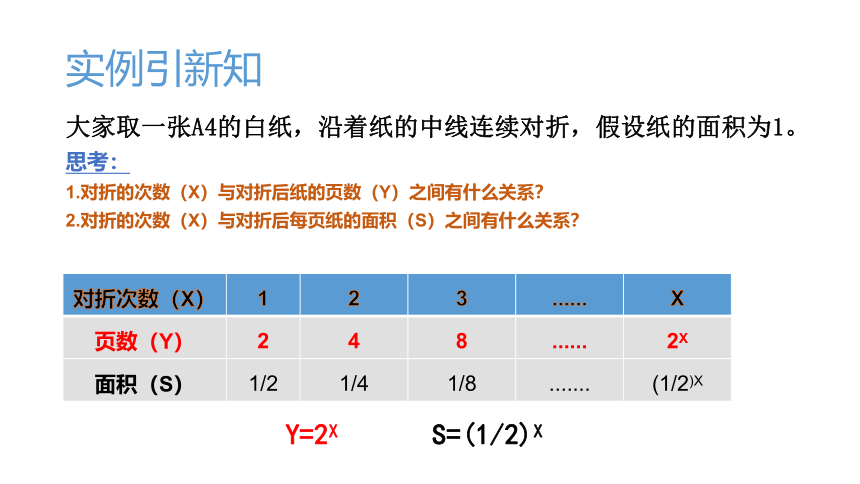
实例引新知
大家取一张A4的白纸,沿着纸的中线连续对折,假设纸的面积为1。
思考:
1.对折的次数(X)与对折后纸的页数(Y)之间有什么关系?
2.对折的次数(X)与对折后每页纸的面积(S)之间有什么关系?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}对折次数(X)
1
2
3
......
X
页数(Y)
2
4
8
......
2X
面积(S)
1/2
1/4
1/8
.......
(1/2)X
Y=2X S=(1/2)X
新知讲解
一、指数函数的定义:
一般的,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域为R。
思考:
1.为什么要规定 a>0,且a≠1 呢?
①a<0时,x取1/2,1/4....等偶次方根时,在实数范围内没有函数值。
②a=0时,当x>0,ax=0;当x<0时,ax无意义。(0的正分数指数幂等于0,0的负分数指数幂无意义)
③a=1时,ax是一个常数,没有研究的必要。
新知讲解
思考:
2.什么样的函数属于指数函数呢?
例1:判断下列函数中,哪些是指数函数?
(1)y=4x; (2)y=x4;
(3)y=-4x; (4)y=(-4)x;
(5)
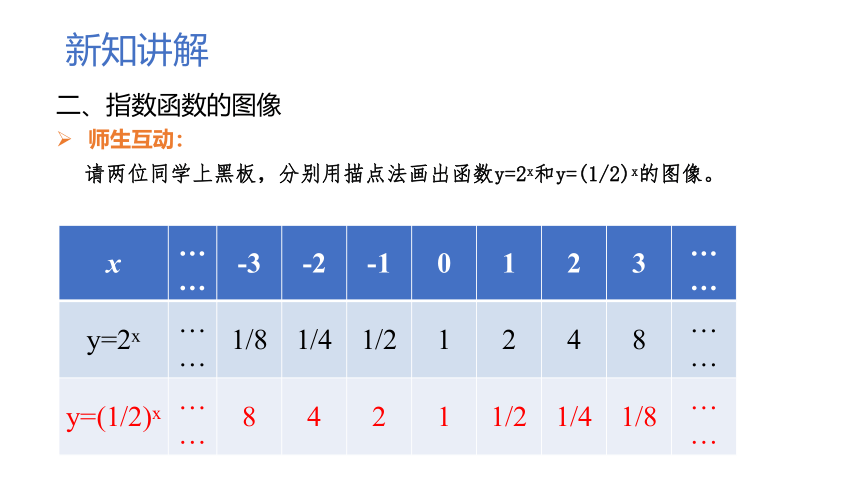
新知讲解
二、指数函数的图像
师生互动:
请两位同学上黑板,分别用描点法画出函数y=2x和y=(1/2)x的图像。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
……
-3
-2
-1
0
1
2
3
……
y=2x
……
1/8
1/4
1/2
1
2
4
8
……
y=(1/2)x
……
8
4
2
1
1/2
1/4
1/8
……
y=2x
x
-3 -2 -1 0 1 2 3
y
8
7
6
5
4
3
2
1
y=(1/2)x
同一坐标系下这两个图有什么关系?
8
7
6
5
4
3
2
1
x
-3 -2 -1 0 1 2 3
y
Y=3x
Y=(1/3)x
新知讲解
三、指数函数的性质
函数
y=ax(a>0且a≠1)
a>1
0图象
定义域
值域
性质
R
(0,+∞)
在(-∞,+∞)上↗
在(-∞,+∞)上↘
图象过定点(0,1)
例3:比较下列各组数值的大小
(1)1.72.5和1.73
(2)0.8-0.1和0.8-0.2
(3)1.70.3和0.93.1
例4:已知下列不等式,比较m,n的大小:
(1)2m<2n;(2)0.2m<0.2n;(3)am课堂总结
本节课学习的内容:
指数函数的概念和意义。
指数函数的图像及性质。
数学思想:
数形结合,归纳思想,分类讨论
一、夯实基础——解下列不等式
(1) 2x>22-x
(2) 32x-1>(1/3)x-2
二、能力提升
如果a-5x>ax+7(a>0,a≠1),求x的取值范围。
课后作业
请各位老师批评指正!
感谢聆听
温故而知新
分数指数幂的运算性质
(1)正分数指数幂的意义:
(2)负分数指数幂与负整数指数幂的意义相仿:
(3)运算性质:(a,b>0,m,n R)
实例引新知
大家取一张A4的白纸,沿着纸的中线连续对折,假设纸的面积为1。
思考:
1.对折的次数(X)与对折后纸的页数(Y)之间有什么关系?
2.对折的次数(X)与对折后每页纸的面积(S)之间有什么关系?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}对折次数(X)
1
2
3
......
X
页数(Y)
2
4
8
......
2X
面积(S)
1/2
1/4
1/8
.......
(1/2)X
Y=2X S=(1/2)X
新知讲解
一、指数函数的定义:
一般的,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域为R。
思考:
1.为什么要规定 a>0,且a≠1 呢?
①a<0时,x取1/2,1/4....等偶次方根时,在实数范围内没有函数值。
②a=0时,当x>0,ax=0;当x<0时,ax无意义。(0的正分数指数幂等于0,0的负分数指数幂无意义)
③a=1时,ax是一个常数,没有研究的必要。
新知讲解
思考:
2.什么样的函数属于指数函数呢?
例1:判断下列函数中,哪些是指数函数?
(1)y=4x; (2)y=x4;
(3)y=-4x; (4)y=(-4)x;
(5)
新知讲解
二、指数函数的图像
师生互动:
请两位同学上黑板,分别用描点法画出函数y=2x和y=(1/2)x的图像。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
……
-3
-2
-1
0
1
2
3
……
y=2x
……
1/8
1/4
1/2
1
2
4
8
……
y=(1/2)x
……
8
4
2
1
1/2
1/4
1/8
……
y=2x
x
-3 -2 -1 0 1 2 3
y
8
7
6
5
4
3
2
1
y=(1/2)x
同一坐标系下这两个图有什么关系?
8
7
6
5
4
3
2
1
x
-3 -2 -1 0 1 2 3
y
Y=3x
Y=(1/3)x
新知讲解
三、指数函数的性质
函数
y=ax(a>0且a≠1)
a>1
0
定义域
值域
性质
R
(0,+∞)
在(-∞,+∞)上↗
在(-∞,+∞)上↘
图象过定点(0,1)
例3:比较下列各组数值的大小
(1)1.72.5和1.73
(2)0.8-0.1和0.8-0.2
(3)1.70.3和0.93.1
例4:已知下列不等式,比较m,n的大小:
(1)2m<2n;(2)0.2m<0.2n;(3)am
本节课学习的内容:
指数函数的概念和意义。
指数函数的图像及性质。
数学思想:
数形结合,归纳思想,分类讨论
一、夯实基础——解下列不等式
(1) 2x>22-x
(2) 32x-1>(1/3)x-2
二、能力提升
如果a-5x>ax+7(a>0,a≠1),求x的取值范围。
课后作业
请各位老师批评指正!
感谢聆听
