沪教版(上海)数学高一下册-5.5 角与名的变换 课件(18张PPT)
文档属性
| 名称 | 沪教版(上海)数学高一下册-5.5 角与名的变换 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 250.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 21:34:53 | ||
图片预览




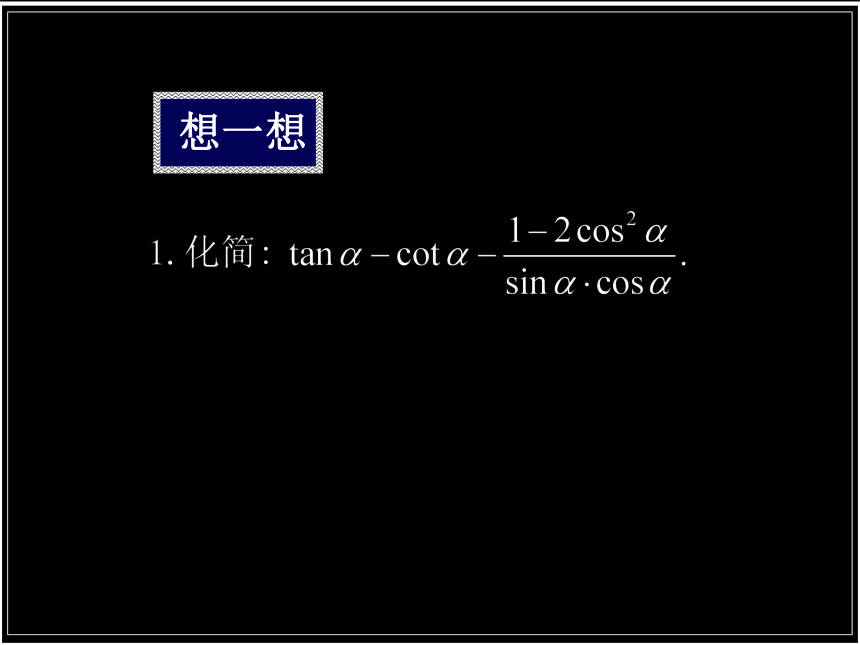

文档简介
三角比中
角与名的变换
复习要求
1. 在理解两角和(差)、二倍角与半角公式的基础上,掌握三角公式之间的变换思想方法.
2. 能将 三角比中“角的变换”、“‘名’的变换”,在化简、求值和恒等式证明等问题中较熟练地应用.
公式 回眸
公式 回眸
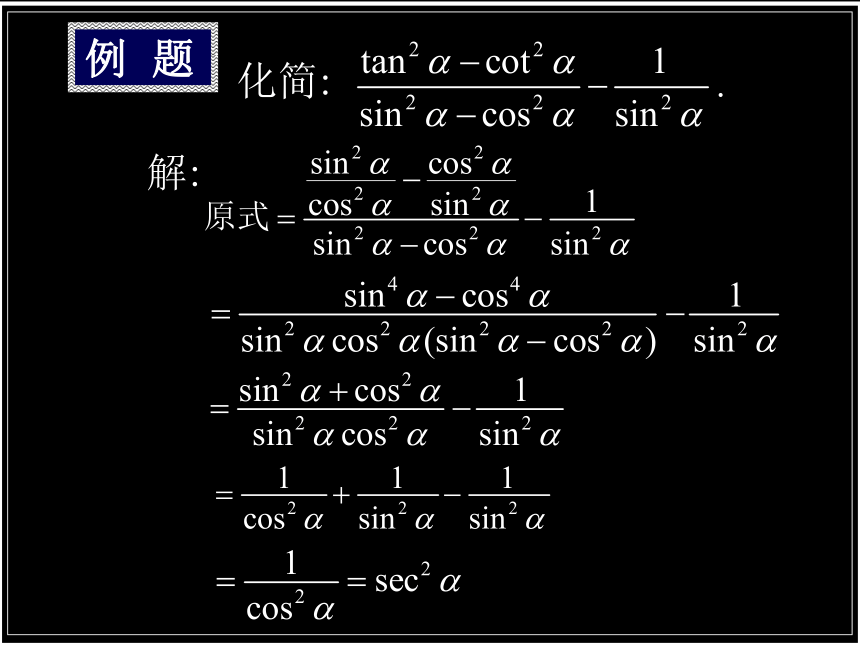
例 题
想一想
在三角变换时,若由于三角名较多给其变形带来困难,则常选定一个三角名为目标,将其余三角名向它转化,以尽可能减少三角名的个数,达到促进三角变换的功效. 常用的有: “切化弦” 、 “弦化切” 、 “正化余”和“余化正” ,这是三角恒等变换的一个策略.
三角比“名”的变换:
例 题
分析:观察条件角和结论角之间的内在联系,可以发现 ,从而进行角的拆分,达到转化的目的.
例 题
练一练
在进行三角比的化简和求值时,常常遇到表达式中出现较多相异的角.这时我们必须首先弄清这些角之间的相互关系,选定一个目标,其余的角都朝着这个目标转化,按题意配出相应的角的和与差、倍与半,创造使用三角公式的条件,以达到化简和论证的目的,这是三角变形的基本策略之一.即:变角和配角.
三角比“角”的变换:
常用“角 ”的 变换,有
和
差
倍
半
例 题
做一做
三角变换的思路与转化
宏观思路
分析差异
寻找联系
促进转化
角的差异
三角比名的差异等
名的正余关系
名的弦切关系
角的和差倍半关系
活用三角公式
选用代数方法
思想方法指导
微观探究
三角比中
名的转化
三角比中
角的转化
把一个表达式变形为另一个和它等价的表达式,变形前后两个表达式对字母的允许值不变,这种“形”变而“值”不变,便是恒等变形的实质,恒等变形的过程,就是对命题连续化简的过程.三角恒等变形的方向和方法主要有:
1.三角函数名的统一
2.”角”的统一
例 题 5:
求:
的 值
分析:注意找出一个“基本量”,将其余的角都化成特殊角与这个“基本量”之间的和、差关系。
复习内 容
理解、记忆三角公式的来龙去脉,并会进行推导,是复习应达到的起码要求.因为公式的推导过程体现了三角变换的一些基本方法与技能、技巧,它是复习本单元的基础.
角与名的变换
复习要求
1. 在理解两角和(差)、二倍角与半角公式的基础上,掌握三角公式之间的变换思想方法.
2. 能将 三角比中“角的变换”、“‘名’的变换”,在化简、求值和恒等式证明等问题中较熟练地应用.
公式 回眸
公式 回眸
例 题
想一想
在三角变换时,若由于三角名较多给其变形带来困难,则常选定一个三角名为目标,将其余三角名向它转化,以尽可能减少三角名的个数,达到促进三角变换的功效. 常用的有: “切化弦” 、 “弦化切” 、 “正化余”和“余化正” ,这是三角恒等变换的一个策略.
三角比“名”的变换:
例 题
分析:观察条件角和结论角之间的内在联系,可以发现 ,从而进行角的拆分,达到转化的目的.
例 题
练一练
在进行三角比的化简和求值时,常常遇到表达式中出现较多相异的角.这时我们必须首先弄清这些角之间的相互关系,选定一个目标,其余的角都朝着这个目标转化,按题意配出相应的角的和与差、倍与半,创造使用三角公式的条件,以达到化简和论证的目的,这是三角变形的基本策略之一.即:变角和配角.
三角比“角”的变换:
常用“角 ”的 变换,有
和
差
倍
半
例 题
做一做
三角变换的思路与转化
宏观思路
分析差异
寻找联系
促进转化
角的差异
三角比名的差异等
名的正余关系
名的弦切关系
角的和差倍半关系
活用三角公式
选用代数方法
思想方法指导
微观探究
三角比中
名的转化
三角比中
角的转化
把一个表达式变形为另一个和它等价的表达式,变形前后两个表达式对字母的允许值不变,这种“形”变而“值”不变,便是恒等变形的实质,恒等变形的过程,就是对命题连续化简的过程.三角恒等变形的方向和方法主要有:
1.三角函数名的统一
2.”角”的统一
例 题 5:
求:
的 值
分析:注意找出一个“基本量”,将其余的角都化成特殊角与这个“基本量”之间的和、差关系。
复习内 容
理解、记忆三角公式的来龙去脉,并会进行推导,是复习应达到的起码要求.因为公式的推导过程体现了三角变换的一些基本方法与技能、技巧,它是复习本单元的基础.
