沪教版数学高一下册-6.1.2正弦函数和余弦函数的图像和性质 -正余弦函数的最值 课件(共16张PPT)
文档属性
| 名称 | 沪教版数学高一下册-6.1.2正弦函数和余弦函数的图像和性质 -正余弦函数的最值 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 765.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 21:37:07 | ||
图片预览


文档简介
6.1.2
正余弦函数的最值
y=Asin(ωx+φ)
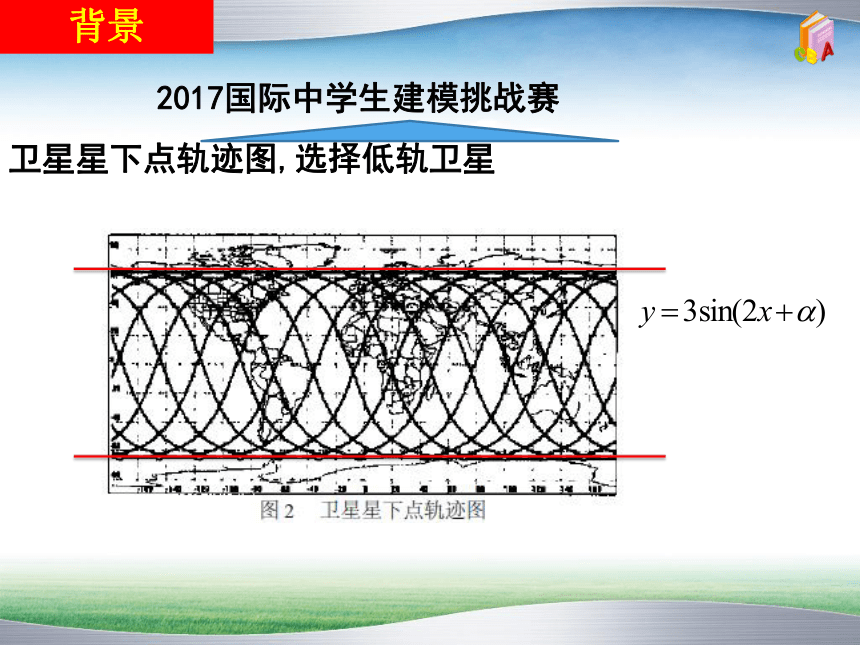
背景
2017国际中学生建模挑战赛
卫星星下点轨迹图,选择低轨卫星
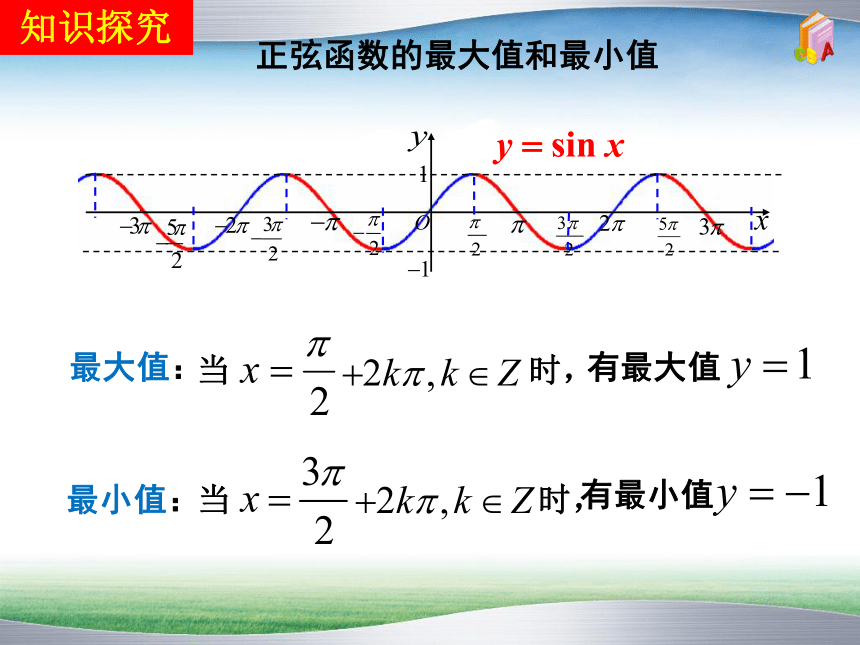
正弦函数的最大值和最小值
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
知识探究
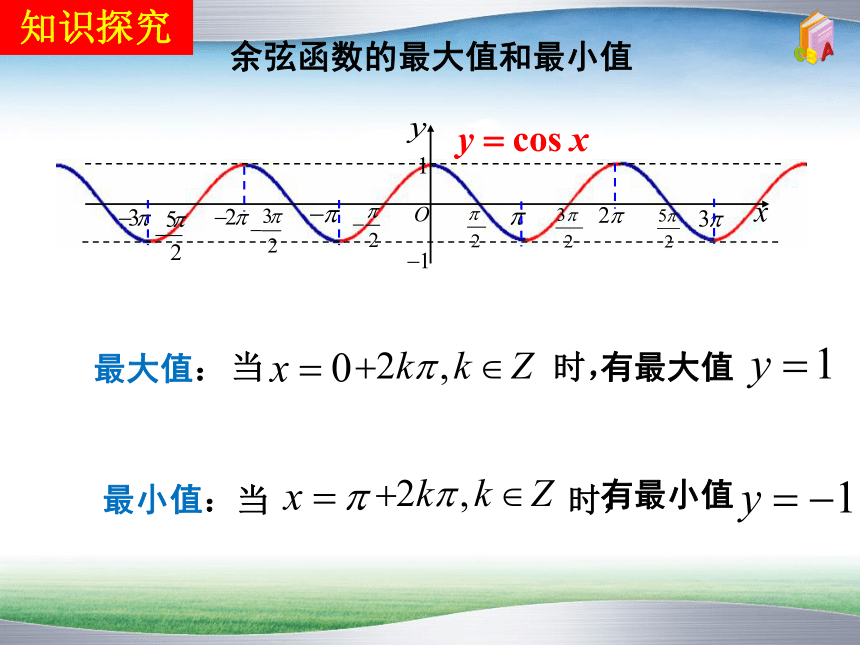
余弦函数的最大值和最小值
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
知识探究
解:
设 ,
则
的最大值为 1,
由
知识运用
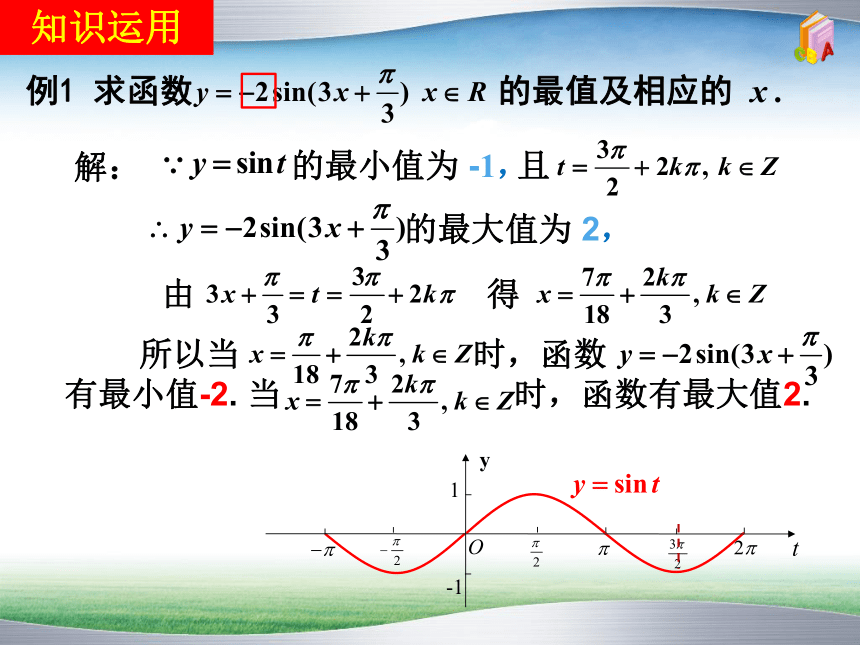
例1 求函数 的最值及相应的 x .
且
的最小值为 -2,
得
t
O
1
y
-1
解:
的最小值为 -1,
由
知识运用
例1 求函数 的最值及相应的 x .
且
的最大值为 2,
得
t
O
1
y
-1
所以当 时,函数 有最小值-2. 当 时,函数有最大值2.
解:
设 ,
则原函数变为 .
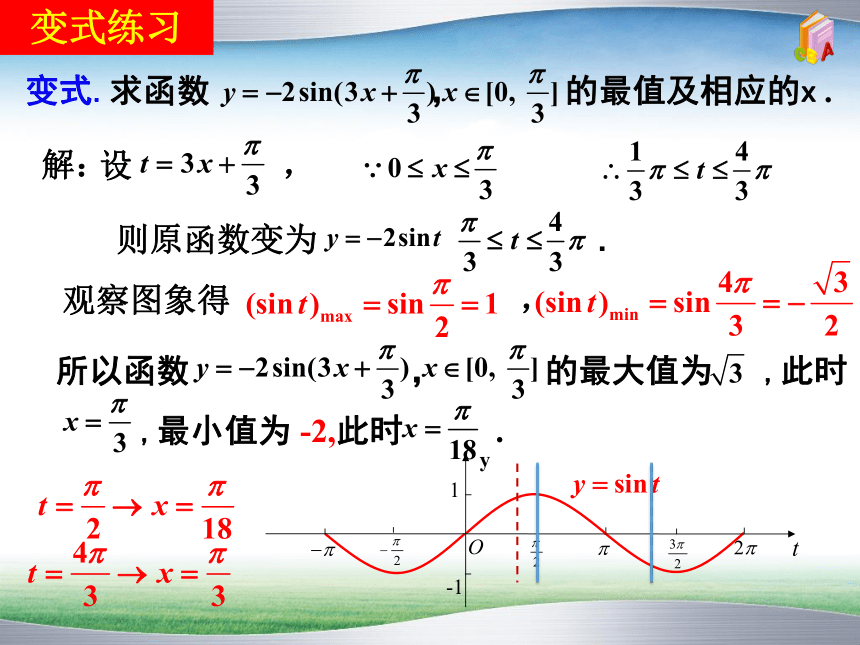
变式.求函数 , 的最值及相应的x .
t
O
1
y
-1
变式练习
观察图象得 ,
所以函数 , 的最大值为 ,此时
,最小值为 -2,此时 .
解:
函数可化为 ,
令
知识运用
例2 求函数 的最值.
则
t
y
-1
-1
1
1
当 函数取最大值
当 函数取最小值
函数可化为
变式运用
1.求函数 的最值.
令
2.求函数 是常数,求最值.
函数可化为
令
3.求函数 是常数,求最值.
函数可化为
令
总结:换元思想在复合函数中的应用
解:
由题意可知
知识运用
例3 如图,矩形 四个顶点分别在矩形
四条边上, 如果 与 夹角为 ,
那么当 为何值时,矩形 的周长最大。
即
同理
因此矩形 周长为
知识运用
又
故当
即 时,取得最大值。
辅助角公式
形如
转化为
X的范围
练一练
1.求函数 的最大(小)值。
借助于二倍角公式
练一练
法一:
2.请在半圆形纸快中裁剪出最大面积的矩形。
练一练
法二:
2.请在半圆形纸快中裁剪出最大面积的矩形。
思考
请在一个扇形纸快中裁剪出最大面积的矩形。
x
6?
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y
当且仅当
当且仅当
当且仅当
当且仅当
正弦、余弦函数的最值
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
课堂小结
正余弦函数的最值
y=Asin(ωx+φ)
背景
2017国际中学生建模挑战赛
卫星星下点轨迹图,选择低轨卫星
正弦函数的最大值和最小值
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
知识探究
余弦函数的最大值和最小值
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
知识探究
解:
设 ,
则
的最大值为 1,
由
知识运用
例1 求函数 的最值及相应的 x .
且
的最小值为 -2,
得
t
O
1
y
-1
解:
的最小值为 -1,
由
知识运用
例1 求函数 的最值及相应的 x .
且
的最大值为 2,
得
t
O
1
y
-1
所以当 时,函数 有最小值-2. 当 时,函数有最大值2.
解:
设 ,
则原函数变为 .
变式.求函数 , 的最值及相应的x .
t
O
1
y
-1
变式练习
观察图象得 ,
所以函数 , 的最大值为 ,此时
,最小值为 -2,此时 .
解:
函数可化为 ,
令
知识运用
例2 求函数 的最值.
则
t
y
-1
-1
1
1
当 函数取最大值
当 函数取最小值
函数可化为
变式运用
1.求函数 的最值.
令
2.求函数 是常数,求最值.
函数可化为
令
3.求函数 是常数,求最值.
函数可化为
令
总结:换元思想在复合函数中的应用
解:
由题意可知
知识运用
例3 如图,矩形 四个顶点分别在矩形
四条边上, 如果 与 夹角为 ,
那么当 为何值时,矩形 的周长最大。
即
同理
因此矩形 周长为
知识运用
又
故当
即 时,取得最大值。
辅助角公式
形如
转化为
X的范围
练一练
1.求函数 的最大(小)值。
借助于二倍角公式
练一练
法一:
2.请在半圆形纸快中裁剪出最大面积的矩形。
练一练
法二:
2.请在半圆形纸快中裁剪出最大面积的矩形。
思考
请在一个扇形纸快中裁剪出最大面积的矩形。
x
6?
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y
当且仅当
当且仅当
当且仅当
当且仅当
正弦、余弦函数的最值
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
课堂小结
