人教高中数学必修二 2.1《空间点-直线-平面之间的位置关系--平面》课件
文档属性
| 名称 | 人教高中数学必修二 2.1《空间点-直线-平面之间的位置关系--平面》课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 08:19:00 | ||
图片预览








文档简介
2.1.1 平面
实例引入
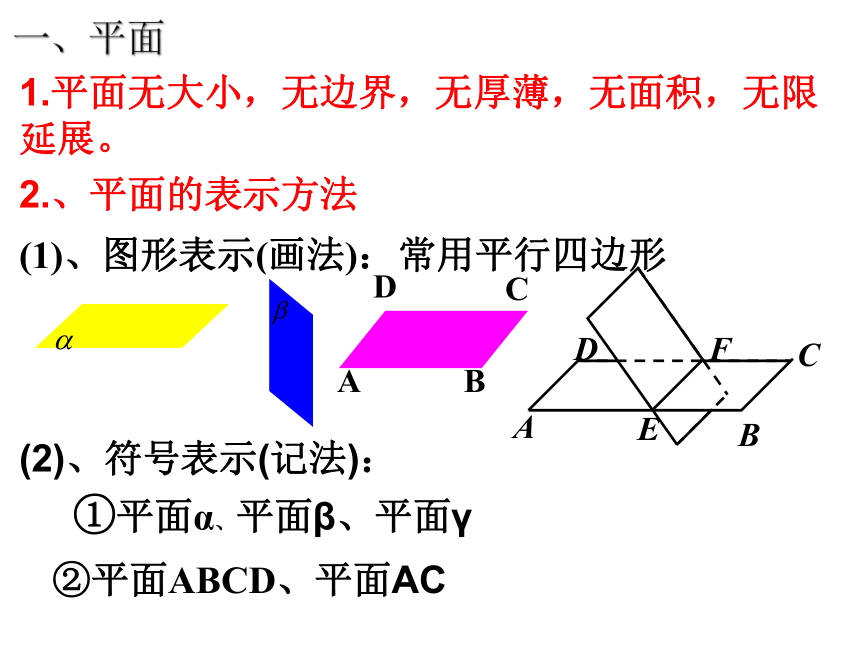
一、平面
1.平面无大小,无边界,无厚薄,无面积,无限延展。
2.、平面的表示方法
(1)、图形表示(画法):
常用平行四边形
A
B
C
D
(2)、符号表示(记法):
①平面α、平面β、平面γ
②平面ABCD、平面AC
A
D
C
B
E
F
图形
符号语言
文字语言(读法)
点在直线上
点不在直线上
点在平面内
点不在平面内
直线a、b交于点A
二、点、线、面的基本位置关系
(1)符号表示:
(2)集合关系:
点A、
线a、
面α
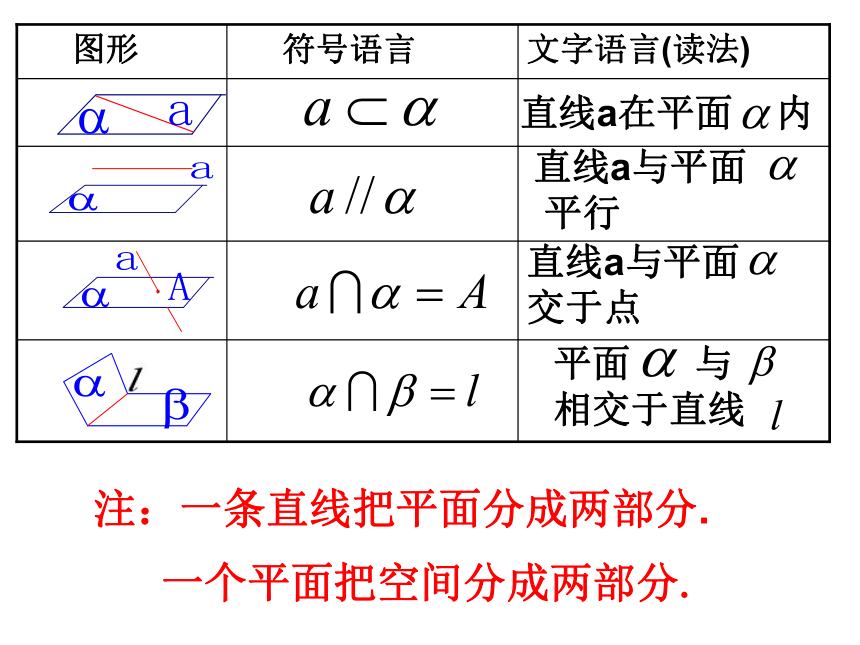
图形
符号语言
文字语言(读法)
直线a在平面 内
直线a与平面
平行
直线a与平面
交于点
平面 与
相交于直线
注:一条直线把平面分成两部分.
一个平面把空间分成两部分.
(2)直线a经过平面 外一点M
(3)直线 在平面 内,又在平面 内
(即平面和平面相交于直线)
(1)点A在平面 内,但不在平面 内
例2. 将下列文字语言转化为符号语言:
1、判断下列各题的说法正确与否,在正
确的说法的题号后打 ,否则打 :
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是 4 cm 2; ( )
5、一个平面可以把空间分成两部分. ( )
练习
如果直线 l 与平面α有一个公共点P,直线 l 是否在平面α内?
平面公理
实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.
平面公理
如果直线 l 与平面α有两个公共点,直线 l 是否在平面α内?
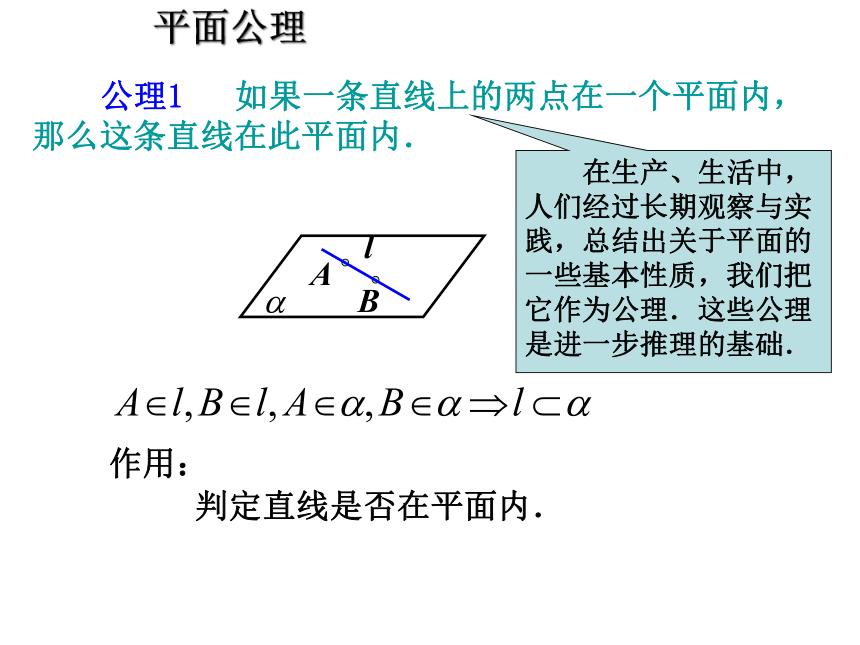
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
A
B
l
作用:
判定直线是否在平面内.
平面公理
在生产、生活中,人们经过长期观察与实践,总结出关于平面的一些基本性质,我们把它作为公理.这些公理是进一步推理的基础.
生活中经常看到用三角架支撑照相机.
平面公理
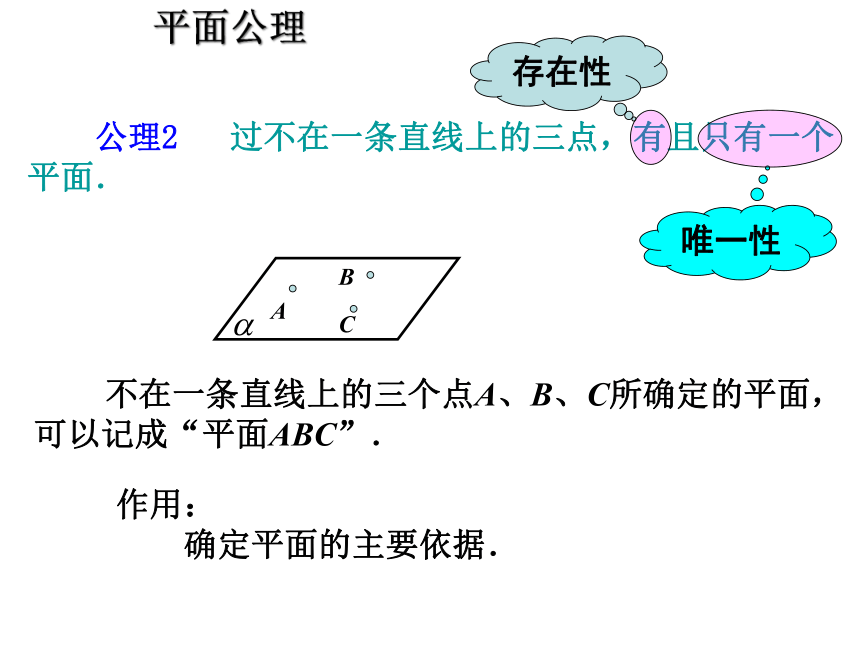
公理2 过不在一条直线上的三点,有且只有一个平面.
A
C
B
存在性
唯一性
作用:
确定平面的主要依据.
平面公理
不在一条直线上的三个点A、B、C所确定的平面,可以记成“平面ABC”.
经过不在同一条直线上的三点,有且只有一个平面。
公理2
A
B
C
公理2的三条推论:
1.经过一条直线和这条直线外一点,有且只有一个平面
2.经过两条相交直线,有且只有一个平面
3.经过两条平行直线,有且只有一个平面
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?
B
平面公理
B
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?
平面公理
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
作用:
①判断两个平面相交的依据.
②判断点在直线上.
l
P
平面公理
例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.
a
l
A
B
a
l
P
b
(1)
(2)
解:在(1)中,
在(2)中,
典型例题
小结
1.平面的概念;
3.点、直线、平面间基本关系的文字语言,图形语言和符号语言之间关系的转换
2.平面的画法、表示方法及两个平面相交的画法;
4.三条公理
2.画画以下四图,看得见的部分用实线描出.
(2)已知A、B、C三点都是平面α与平面β的公共点,且α与β是两个不同的平面;
练习6.(1)在平面 内有A,O,B三点,在平面β内有B,O,C三点,试画出它们的图形
(3)两个平面的公共点的个数可能有 ( )
(4)三个平面两两相交,则它们交线的条数 ( )
A.0 B.1 C.2 D.0或无数
A.最多4条最少3条 B.最多3条最少1条
C.最多3条最少2条 D.最多2条最少1条
(5)已知空间四点中,无三点共线,则可确定
A.一个平面 B.四个平面
C.一个或四个平面 D.无法确定平面的个数
③四条线段顺次首尾连接,所得的图形一定是平面图形吗?
为什么?
练习
①为什么有的自行车后轮旁只安装一只撑脚?
②三角形、梯形是否一定是平面图形?为什么?
④用符号表示下列语句,并画出图形:
⑴点A在平面α内,点B在平面α外;
⑵直线 在平面α内,直线m不在平面α内;
⑶平面α和β相交于直线 ;
⑷直线 经过平面α外一点P和平面α内一点Q ;
⑸直线 是平面α和β的交线,直线m在平面α内,
和m相交于点P.
例1.将下列符号语言转化为图形语言:
(1)
(2)
说明:画图的顺序:先画大件(平面),再画小件(点、线)
,
,
,
,
,
,
,
观察长方体,你能发现长方体的两个相交平面有没有公共直线吗?
这条公共直线B’C’叫做这两个平面A’B’C’D’和平面BB’C’C的交线.
另一方面,相邻两个平面有一个公共点,如平面A’B’C’D’和平面BB’C’C有一个公共点B’,经过点B有且只有一条过该点的公共直线B’C’.
平面公理
在正方体 中,判断下列命题是否正确,并说明理由:
①直线 在平面 内;
错误
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
②设正方形ABCD与 的中心分别为O, ,则平面 与平面 的交线为 ;
正确
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
③由点A,O,C可以确定一个平面;
错误
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
④由 确定的平面是 ;
⑤由 确定的平面与由 确定的平面是同一个平面.
正确
正确
随堂练习
课堂练习:课本P44?练习1、2、3、4
补练:
①有三个公共点的两个平面重合
②梯形的四个顶点在同一个平面内
③三条互相平行的直线必共面
④ 四条线段顺次首尾连接,构成平面图形
2、下列命题正确的是 ( )
A、两条直线可以确定一个平面
B、一条直线和一个点可以确定一个平面
C、空间不同的三点可以确定一个平面
D、两条相交直线可以确定一个平面
1、下列命题中,正确的命题是( )
A、圆上三点可以确定一个平面
B、圆心和圆上两点可确定一个平面
C、四条平行直线不能确定五个平面
D、空间四点中,若四点不共面,则任意三点不共线
4、若给定空间三条直线共面的条件,这四个条
件中不正确的是( )
①三条直线两两相交 ② 三条直线两两平行
③三条直线中有两条平行 ④三条直线共点
3、在空间中,下列命题错误的是( )
5、根据下列条件画出图形:平面α∩平面β=AB
直线a∈α,直线b∈β,a∥AB,b∥AB
6、如图、A∈α,直线AB和AC不在α内,画出AB和AC所确定的平面β,并画出直线BC和平面α的交点.
B
C
A
α
空间图形
文字叙述
符号表示
知识小结
实例引入平面
平面的画法和表示
点和平面的位置关系
平面三个公理
平 面
第二课时
复习巩固:
1.公理1:
作用
2:公理2:
推论:
作用
3.公理3:
作用
如果一条直线上的两点在一个平面内,那么这条直线在此平面内
:判定直线是否在平面内
经过不在同一条直线上的三点,有且只有一个平面
经过一条直线和这条直线外一点(两条相交直线,两条平行直线),有且只有一个平面
确定平面的依据
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
:
①判断两个平面相交的依据.
②判断点在直线上.
一、证明点,线共面的方法:
二、证明点共线的方法:
三、证明线共点的方法:
1.先确定一个平面,后证其余的点和线在该平面内.
2.作多个平面后证重合.(同一法)
1.先找出两个平面,后证点都是两平面的公共点,则点都在交线上。
2.先选择两点确定两平面的交线,后证其余点是两平面的公共点,也在该直线上。
先确定两直线交于一点,再证该点在第三条线上。
E
H
G
F
A
B
C
D
观察长方体,你能发现长方体的顶点,棱所在的直线,以及侧面、底面之间的位置关系吗?
空间点、直线、平面的位置关系
实例引入
一、平面
1.平面无大小,无边界,无厚薄,无面积,无限延展。
2.、平面的表示方法
(1)、图形表示(画法):
常用平行四边形
A
B
C
D
(2)、符号表示(记法):
①平面α、平面β、平面γ
②平面ABCD、平面AC
A
D
C
B
E
F
图形
符号语言
文字语言(读法)
点在直线上
点不在直线上
点在平面内
点不在平面内
直线a、b交于点A
二、点、线、面的基本位置关系
(1)符号表示:
(2)集合关系:
点A、
线a、
面α
图形
符号语言
文字语言(读法)
直线a在平面 内
直线a与平面
平行
直线a与平面
交于点
平面 与
相交于直线
注:一条直线把平面分成两部分.
一个平面把空间分成两部分.
(2)直线a经过平面 外一点M
(3)直线 在平面 内,又在平面 内
(即平面和平面相交于直线)
(1)点A在平面 内,但不在平面 内
例2. 将下列文字语言转化为符号语言:
1、判断下列各题的说法正确与否,在正
确的说法的题号后打 ,否则打 :
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是 4 cm 2; ( )
5、一个平面可以把空间分成两部分. ( )
练习
如果直线 l 与平面α有一个公共点P,直线 l 是否在平面α内?
平面公理
实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.
平面公理
如果直线 l 与平面α有两个公共点,直线 l 是否在平面α内?
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
A
B
l
作用:
判定直线是否在平面内.
平面公理
在生产、生活中,人们经过长期观察与实践,总结出关于平面的一些基本性质,我们把它作为公理.这些公理是进一步推理的基础.
生活中经常看到用三角架支撑照相机.
平面公理
公理2 过不在一条直线上的三点,有且只有一个平面.
A
C
B
存在性
唯一性
作用:
确定平面的主要依据.
平面公理
不在一条直线上的三个点A、B、C所确定的平面,可以记成“平面ABC”.
经过不在同一条直线上的三点,有且只有一个平面。
公理2
A
B
C
公理2的三条推论:
1.经过一条直线和这条直线外一点,有且只有一个平面
2.经过两条相交直线,有且只有一个平面
3.经过两条平行直线,有且只有一个平面
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?
B
平面公理
B
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?
平面公理
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
作用:
①判断两个平面相交的依据.
②判断点在直线上.
l
P
平面公理
例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.
a
l
A
B
a
l
P
b
(1)
(2)
解:在(1)中,
在(2)中,
典型例题
小结
1.平面的概念;
3.点、直线、平面间基本关系的文字语言,图形语言和符号语言之间关系的转换
2.平面的画法、表示方法及两个平面相交的画法;
4.三条公理
2.画画以下四图,看得见的部分用实线描出.
(2)已知A、B、C三点都是平面α与平面β的公共点,且α与β是两个不同的平面;
练习6.(1)在平面 内有A,O,B三点,在平面β内有B,O,C三点,试画出它们的图形
(3)两个平面的公共点的个数可能有 ( )
(4)三个平面两两相交,则它们交线的条数 ( )
A.0 B.1 C.2 D.0或无数
A.最多4条最少3条 B.最多3条最少1条
C.最多3条最少2条 D.最多2条最少1条
(5)已知空间四点中,无三点共线,则可确定
A.一个平面 B.四个平面
C.一个或四个平面 D.无法确定平面的个数
③四条线段顺次首尾连接,所得的图形一定是平面图形吗?
为什么?
练习
①为什么有的自行车后轮旁只安装一只撑脚?
②三角形、梯形是否一定是平面图形?为什么?
④用符号表示下列语句,并画出图形:
⑴点A在平面α内,点B在平面α外;
⑵直线 在平面α内,直线m不在平面α内;
⑶平面α和β相交于直线 ;
⑷直线 经过平面α外一点P和平面α内一点Q ;
⑸直线 是平面α和β的交线,直线m在平面α内,
和m相交于点P.
例1.将下列符号语言转化为图形语言:
(1)
(2)
说明:画图的顺序:先画大件(平面),再画小件(点、线)
,
,
,
,
,
,
,
观察长方体,你能发现长方体的两个相交平面有没有公共直线吗?
这条公共直线B’C’叫做这两个平面A’B’C’D’和平面BB’C’C的交线.
另一方面,相邻两个平面有一个公共点,如平面A’B’C’D’和平面BB’C’C有一个公共点B’,经过点B有且只有一条过该点的公共直线B’C’.
平面公理
在正方体 中,判断下列命题是否正确,并说明理由:
①直线 在平面 内;
错误
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
②设正方形ABCD与 的中心分别为O, ,则平面 与平面 的交线为 ;
正确
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
③由点A,O,C可以确定一个平面;
错误
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
④由 确定的平面是 ;
⑤由 确定的平面与由 确定的平面是同一个平面.
正确
正确
随堂练习
课堂练习:课本P44?练习1、2、3、4
补练:
①有三个公共点的两个平面重合
②梯形的四个顶点在同一个平面内
③三条互相平行的直线必共面
④ 四条线段顺次首尾连接,构成平面图形
2、下列命题正确的是 ( )
A、两条直线可以确定一个平面
B、一条直线和一个点可以确定一个平面
C、空间不同的三点可以确定一个平面
D、两条相交直线可以确定一个平面
1、下列命题中,正确的命题是( )
A、圆上三点可以确定一个平面
B、圆心和圆上两点可确定一个平面
C、四条平行直线不能确定五个平面
D、空间四点中,若四点不共面,则任意三点不共线
4、若给定空间三条直线共面的条件,这四个条
件中不正确的是( )
①三条直线两两相交 ② 三条直线两两平行
③三条直线中有两条平行 ④三条直线共点
3、在空间中,下列命题错误的是( )
5、根据下列条件画出图形:平面α∩平面β=AB
直线a∈α,直线b∈β,a∥AB,b∥AB
6、如图、A∈α,直线AB和AC不在α内,画出AB和AC所确定的平面β,并画出直线BC和平面α的交点.
B
C
A
α
空间图形
文字叙述
符号表示
知识小结
实例引入平面
平面的画法和表示
点和平面的位置关系
平面三个公理
平 面
第二课时
复习巩固:
1.公理1:
作用
2:公理2:
推论:
作用
3.公理3:
作用
如果一条直线上的两点在一个平面内,那么这条直线在此平面内
:判定直线是否在平面内
经过不在同一条直线上的三点,有且只有一个平面
经过一条直线和这条直线外一点(两条相交直线,两条平行直线),有且只有一个平面
确定平面的依据
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
:
①判断两个平面相交的依据.
②判断点在直线上.
一、证明点,线共面的方法:
二、证明点共线的方法:
三、证明线共点的方法:
1.先确定一个平面,后证其余的点和线在该平面内.
2.作多个平面后证重合.(同一法)
1.先找出两个平面,后证点都是两平面的公共点,则点都在交线上。
2.先选择两点确定两平面的交线,后证其余点是两平面的公共点,也在该直线上。
先确定两直线交于一点,再证该点在第三条线上。
E
H
G
F
A
B
C
D
观察长方体,你能发现长方体的顶点,棱所在的直线,以及侧面、底面之间的位置关系吗?
空间点、直线、平面的位置关系
