人教版数学八年级上册12.2再探三角形全等的条件 教学设计(表格式)
文档属性
| 名称 | 人教版数学八年级上册12.2再探三角形全等的条件 教学设计(表格式) |  | |
| 格式 | zip | ||
| 文件大小 | 543.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 09:24:19 | ||
图片预览


文档简介
课程基本信息
课题
再探三角形全等的条件
教科书
书名:
义务教育教科书八年级上册
出版社:
人民教育出版社
出版日期:2013
年6
月
教学目标
教学目标:
梳理全等三角形判定方法的探究过程,能提出关于“SSA能否成为全等判定方法”的问题,并分类进行证明或证伪.
经历提出问题、证明猜想、构造反例的过程,体会数学结论的生成过程,培养学生提出问题、解决问题的能力.
教学重点:
分类讨论两边一对角(SSA)分别相等的两个三角形是否全等.
教学难点:
构造反例、归纳结论.
教学过程
时间
教学环节
主要师生活动
2min
引入
通过前面的学习,我们一起,经历了一次数学家探索三角形全等条件的过程——首先,由全等三角形的定义可知,满足三条边分别相等,三个角分别相等的两个三角形全等.
但同时满足6个条件,似乎过于苛刻和繁琐.
于是提出探究的方向:
如果能用较少的条件,就能简洁地判断两个三角形全等,那会是几组条件呢?
通过实验,我们得到三组条件就能保证两个三角形全等.
那么,从边、角出发,满足三组条件的所有情况,我们是否在之前的学习中都讨论完全了呢?
并没有
下面,我们就一起再探三角形全等的条件,或许会有新的发现!
6min
新课
提出问题
问题1:从边、角出发的三组条件,应该有几种不同的组合?
由单一条件构成:SSS或AAA
由边、角的复合条件构成:
①两角一边AAS或ASA
②两边一角SAS或SSA
理论上,共有6种不同的组合.
问题2:其中哪种组合是最容易被同学否定的呢?
AAA是最容易被否定的.
例如,任作两个等腰直角三角形,满足三组角均相等.形状能被确定,但由于缺少边的条件,大小不定,故不能保证二者全等.
这样,剩下的组合中,无论成立与否,我们发现,要想成为全等三角形的判定,都至少要有一组边的条件.
和我们已经探究得到的5种判定方法相比,对于任意三角形,有4种判定方法:SSS、SAS、ASA、AAS;对直角三角形,还多了一种特殊的HL.
HL表面上只需要斜边、直角边两组条件,但由于多了直角的前提,实则也是3个条件,可以并入“两边一对角分别相等”的情况.
提出问题
分析到这里,我们会有这样的疑问:
SSA能否在非直角三角形判定全等时也成立呢?
进行探究
要想解决这个问题,按照我们对于几何学习的经验,首先要提出猜想:两组边及一边的对角分别相等的两个三角形全等.
下面,我们对这个猜想进行证明或证伪.
前面的学习中,我们积累了这样的经验:三角形的全等条件就是确定三角形的形状和大小的条件,根据这一思路,两边一对角分别相等的两个三角形是否全等的问题,可以转化为两边一对角是否能确定三角形的形状和大小的问题.
从这个角度出发,可进行讨论如下:
我们要先将问题进行数学化地叙述,以便研究.
已知:在三角形中,两边为a,b,边a的对角为α
我们已经探究过直角三角形的情况,现在,可以从它出发展开研究.
当α=90°时
先作射线AP、AQ使其夹角为90°(如图1-1)
再任作线段a,b
(a>b)
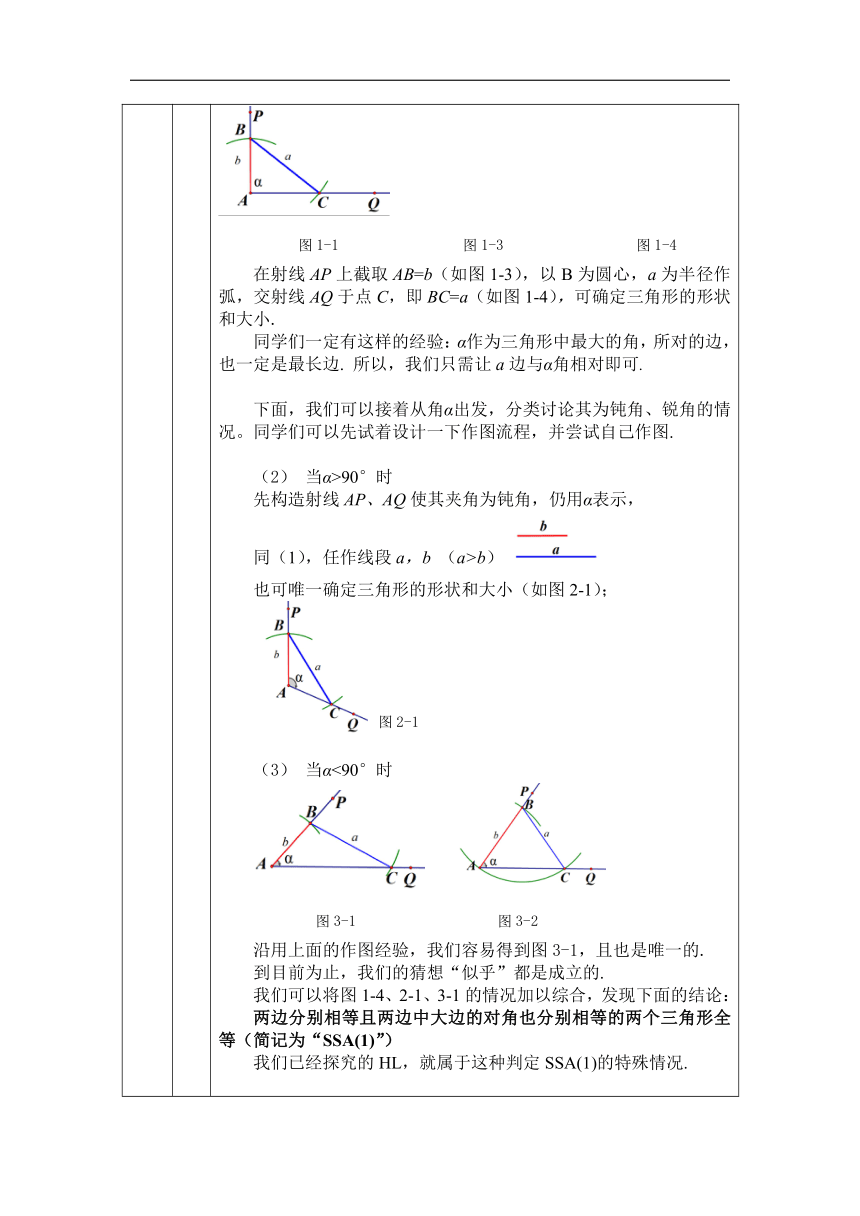
在射线AP上截取AB=b(如图1-3),以B为圆心,a为半径作弧,交射线AQ于点C,即BC=a(如图1-4),可确定三角形的形状和大小.
同学们一定有这样的经验:α作为三角形中最大的角,所对的边,也一定是最长边.
所以,我们只需让a边与α角相对即可.
下面,我们可以接着从角α出发,分类讨论其为钝角、锐角的情况。同学们可以先试着设计一下作图流程,并尝试自己作图.
当α>90°时
先构造射线AP、AQ使其夹角为钝角,仍用α表示,
同(1),任作线段a,b
(a>b)
也可唯一确定三角形的形状和大小(如图2-1);
当α<90°时
沿用上面的作图经验,我们容易得到图3-1,且也是唯一的.
到目前为止,我们的猜想“似乎”都是成立的.
我们可以将图1-4、2-1、3-1的情况加以综合,发现下面的结论:
两边分别相等且两边中大边的对角也分别相等的两个三角形全等(简记为“SSA(1)”)
我们已经探究的HL,就属于这种判定SSA(1)的特殊情况.
注意,这里是假设a>b的情况。
如果a不变,b变长,当a=b时,如图3-2所示,以B为圆心,a为半径作弧,与射线AQ存在两个交点,其中一个交点与点A重合,不能构成三角形,另一个交点为C,得到三角形的形状,也是确定的.
当a我们发现,三角形由不能唯一确定(图3-3)到唯一确定(图3-4),最后,由于b变得太大,以B为圆心a为半径作弧时,无法与射线AQ相交,三角形不存在了(图3-5).
至此,回顾一下,我们的讨论是否完全?
我们以“两边一对角”中的“一对角”α作为分类的第一层标准,按照α为钝角、直角和锐角三种情况展开讨论;每一种讨论中,又对“两边一对角”中的“两边”a、b谁为α所对的较长边,展开第二个层次的讨论,故讨论是完全的.
我们发现:
其实,两边一对角分别相等的两个三角形,在多数情形下是全等的,只有一种情况不能确定三角形的形状,就是图3-3的情况.
此时,a随着学习的深入,我们会知道,当a归纳小结
下面,我们梳理一下今天的探究的过程,结合图形归纳我们的结论.
已知:在三角形中,两边为a,b,边a的对角为α
SSA成立的情况:
α>90°
α=90°
当α≥90°时
由a,b,α可确定三角形的形状和大小,其中α=90°时,就是我们熟悉的HL.
(2)当α<90°时
①若a>b或a=b,由a,b,α可确定三角形的形状和大小
a>b
a=b
②若a<b且a等于点B到AQ的距离时,由a,b,α可确定三角形的形状和大小.
SSA不成立的情况:
当α<90°,
a<b且a大于点B到AQ的距离时,从图中我们能直观地看出,长边b的对角一个是钝角,一个是锐角,两个三角形显然是不全等的.
同学们在心里,一定为“SSA”鸣不平吧:
差一点儿就能升级成世界公认的判定定理了!但因为这一点瑕疵,该结论就不具有普适性了.这也正体现了数学的严谨和科学,不是吗?
补充思考
三组条件的情况,我们已经进行了较为深入地研究,至此,同学们可能会有这样的想法:如果条件多于三组,应该会更保险些吧?
曾经有一位中学的数学教师向数学家赵访熊教授请教:如果一个三角形,有五个元素与另一个三角形的五个元素两两相等,这两个三角形是否全等?
同学们,你们认为全等吗?
赵教授的答案是:不一定
我们来看举出的反例:
如图,在△ABC与△DEF中,AC=DE,BC=DF,∠A=∠D,
∠B=∠E,∠C=∠F,两个三角形有5个元素两两相等,但这两个三角形显然不全等.
从反例的构造中我们发现,三角形的形状不难任意给出,但要保证还有两条边分别相等,边的长度就要有限制了,至于为什么是8、12、18、27这组数,或者还有哪些符合条件的数可以构成这样的两个三角形,就需要更多的数学知识了.感兴趣的同学,可以查阅相关资料,继续探讨.
由此看来,如果三角形的角或边不是对应相等的关系,即使两两相等的元素再多,也不一定有全等关系.
小结
同学们,今天,我们虽然没有探究出新的方法来判定两个三角形全等,但我们发现两边一对角分别相等的两个三角形,在哪些情形下是可以判定全等的.虽然我们发现的结论不能称为定理,也不能在解题中直接使用,但探究的过程、分类的依据、讨论的完备,都非常有意义.我们可以沿用今天的思路,去发现、验证我们在几何学习中的其他猜想.
记住,珍视自己的每一个质疑,它们都承载着人类的智慧哦.
作业
阅读教材P46-47
借助几何画板,或通过尺规作图,试着复盘今天探究的过程吧,把你的发现,整理在作业本上.
课题
再探三角形全等的条件
教科书
书名:
义务教育教科书八年级上册
出版社:
人民教育出版社
出版日期:2013
年6
月
教学目标
教学目标:
梳理全等三角形判定方法的探究过程,能提出关于“SSA能否成为全等判定方法”的问题,并分类进行证明或证伪.
经历提出问题、证明猜想、构造反例的过程,体会数学结论的生成过程,培养学生提出问题、解决问题的能力.
教学重点:
分类讨论两边一对角(SSA)分别相等的两个三角形是否全等.
教学难点:
构造反例、归纳结论.
教学过程
时间
教学环节
主要师生活动
2min
引入
通过前面的学习,我们一起,经历了一次数学家探索三角形全等条件的过程——首先,由全等三角形的定义可知,满足三条边分别相等,三个角分别相等的两个三角形全等.
但同时满足6个条件,似乎过于苛刻和繁琐.
于是提出探究的方向:
如果能用较少的条件,就能简洁地判断两个三角形全等,那会是几组条件呢?
通过实验,我们得到三组条件就能保证两个三角形全等.
那么,从边、角出发,满足三组条件的所有情况,我们是否在之前的学习中都讨论完全了呢?
并没有
下面,我们就一起再探三角形全等的条件,或许会有新的发现!
6min
新课
提出问题
问题1:从边、角出发的三组条件,应该有几种不同的组合?
由单一条件构成:SSS或AAA
由边、角的复合条件构成:
①两角一边AAS或ASA
②两边一角SAS或SSA
理论上,共有6种不同的组合.
问题2:其中哪种组合是最容易被同学否定的呢?
AAA是最容易被否定的.
例如,任作两个等腰直角三角形,满足三组角均相等.形状能被确定,但由于缺少边的条件,大小不定,故不能保证二者全等.
这样,剩下的组合中,无论成立与否,我们发现,要想成为全等三角形的判定,都至少要有一组边的条件.
和我们已经探究得到的5种判定方法相比,对于任意三角形,有4种判定方法:SSS、SAS、ASA、AAS;对直角三角形,还多了一种特殊的HL.
HL表面上只需要斜边、直角边两组条件,但由于多了直角的前提,实则也是3个条件,可以并入“两边一对角分别相等”的情况.
提出问题
分析到这里,我们会有这样的疑问:
SSA能否在非直角三角形判定全等时也成立呢?
进行探究
要想解决这个问题,按照我们对于几何学习的经验,首先要提出猜想:两组边及一边的对角分别相等的两个三角形全等.
下面,我们对这个猜想进行证明或证伪.
前面的学习中,我们积累了这样的经验:三角形的全等条件就是确定三角形的形状和大小的条件,根据这一思路,两边一对角分别相等的两个三角形是否全等的问题,可以转化为两边一对角是否能确定三角形的形状和大小的问题.
从这个角度出发,可进行讨论如下:
我们要先将问题进行数学化地叙述,以便研究.
已知:在三角形中,两边为a,b,边a的对角为α
我们已经探究过直角三角形的情况,现在,可以从它出发展开研究.
当α=90°时
先作射线AP、AQ使其夹角为90°(如图1-1)
再任作线段a,b
(a>b)
在射线AP上截取AB=b(如图1-3),以B为圆心,a为半径作弧,交射线AQ于点C,即BC=a(如图1-4),可确定三角形的形状和大小.
同学们一定有这样的经验:α作为三角形中最大的角,所对的边,也一定是最长边.
所以,我们只需让a边与α角相对即可.
下面,我们可以接着从角α出发,分类讨论其为钝角、锐角的情况。同学们可以先试着设计一下作图流程,并尝试自己作图.
当α>90°时
先构造射线AP、AQ使其夹角为钝角,仍用α表示,
同(1),任作线段a,b
(a>b)
也可唯一确定三角形的形状和大小(如图2-1);
当α<90°时
沿用上面的作图经验,我们容易得到图3-1,且也是唯一的.
到目前为止,我们的猜想“似乎”都是成立的.
我们可以将图1-4、2-1、3-1的情况加以综合,发现下面的结论:
两边分别相等且两边中大边的对角也分别相等的两个三角形全等(简记为“SSA(1)”)
我们已经探究的HL,就属于这种判定SSA(1)的特殊情况.
注意,这里是假设a>b的情况。
如果a不变,b变长,当a=b时,如图3-2所示,以B为圆心,a为半径作弧,与射线AQ存在两个交点,其中一个交点与点A重合,不能构成三角形,另一个交点为C,得到三角形的形状,也是确定的.
当a
至此,回顾一下,我们的讨论是否完全?
我们以“两边一对角”中的“一对角”α作为分类的第一层标准,按照α为钝角、直角和锐角三种情况展开讨论;每一种讨论中,又对“两边一对角”中的“两边”a、b谁为α所对的较长边,展开第二个层次的讨论,故讨论是完全的.
我们发现:
其实,两边一对角分别相等的两个三角形,在多数情形下是全等的,只有一种情况不能确定三角形的形状,就是图3-3的情况.
此时,a
下面,我们梳理一下今天的探究的过程,结合图形归纳我们的结论.
已知:在三角形中,两边为a,b,边a的对角为α
SSA成立的情况:
α>90°
α=90°
当α≥90°时
由a,b,α可确定三角形的形状和大小,其中α=90°时,就是我们熟悉的HL.
(2)当α<90°时
①若a>b或a=b,由a,b,α可确定三角形的形状和大小
a>b
a=b
②若a<b且a等于点B到AQ的距离时,由a,b,α可确定三角形的形状和大小.
SSA不成立的情况:
当α<90°,
a<b且a大于点B到AQ的距离时,从图中我们能直观地看出,长边b的对角一个是钝角,一个是锐角,两个三角形显然是不全等的.
同学们在心里,一定为“SSA”鸣不平吧:
差一点儿就能升级成世界公认的判定定理了!但因为这一点瑕疵,该结论就不具有普适性了.这也正体现了数学的严谨和科学,不是吗?
补充思考
三组条件的情况,我们已经进行了较为深入地研究,至此,同学们可能会有这样的想法:如果条件多于三组,应该会更保险些吧?
曾经有一位中学的数学教师向数学家赵访熊教授请教:如果一个三角形,有五个元素与另一个三角形的五个元素两两相等,这两个三角形是否全等?
同学们,你们认为全等吗?
赵教授的答案是:不一定
我们来看举出的反例:
如图,在△ABC与△DEF中,AC=DE,BC=DF,∠A=∠D,
∠B=∠E,∠C=∠F,两个三角形有5个元素两两相等,但这两个三角形显然不全等.
从反例的构造中我们发现,三角形的形状不难任意给出,但要保证还有两条边分别相等,边的长度就要有限制了,至于为什么是8、12、18、27这组数,或者还有哪些符合条件的数可以构成这样的两个三角形,就需要更多的数学知识了.感兴趣的同学,可以查阅相关资料,继续探讨.
由此看来,如果三角形的角或边不是对应相等的关系,即使两两相等的元素再多,也不一定有全等关系.
小结
同学们,今天,我们虽然没有探究出新的方法来判定两个三角形全等,但我们发现两边一对角分别相等的两个三角形,在哪些情形下是可以判定全等的.虽然我们发现的结论不能称为定理,也不能在解题中直接使用,但探究的过程、分类的依据、讨论的完备,都非常有意义.我们可以沿用今天的思路,去发现、验证我们在几何学习中的其他猜想.
记住,珍视自己的每一个质疑,它们都承载着人类的智慧哦.
作业
阅读教材P46-47
借助几何画板,或通过尺规作图,试着复盘今天探究的过程吧,把你的发现,整理在作业本上.
