27.2.3相似三角形的应用举例 (含答案)
文档属性
| 名称 | 27.2.3相似三角形的应用举例 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 541.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览

文档简介
27.2.3相似三角形的应用举例
自主预习
1.在同一时刻同一个地点物体的高度与自身的影长的关系是( )
A.成反比例 B.成正比例 C.相等 D.不成比例
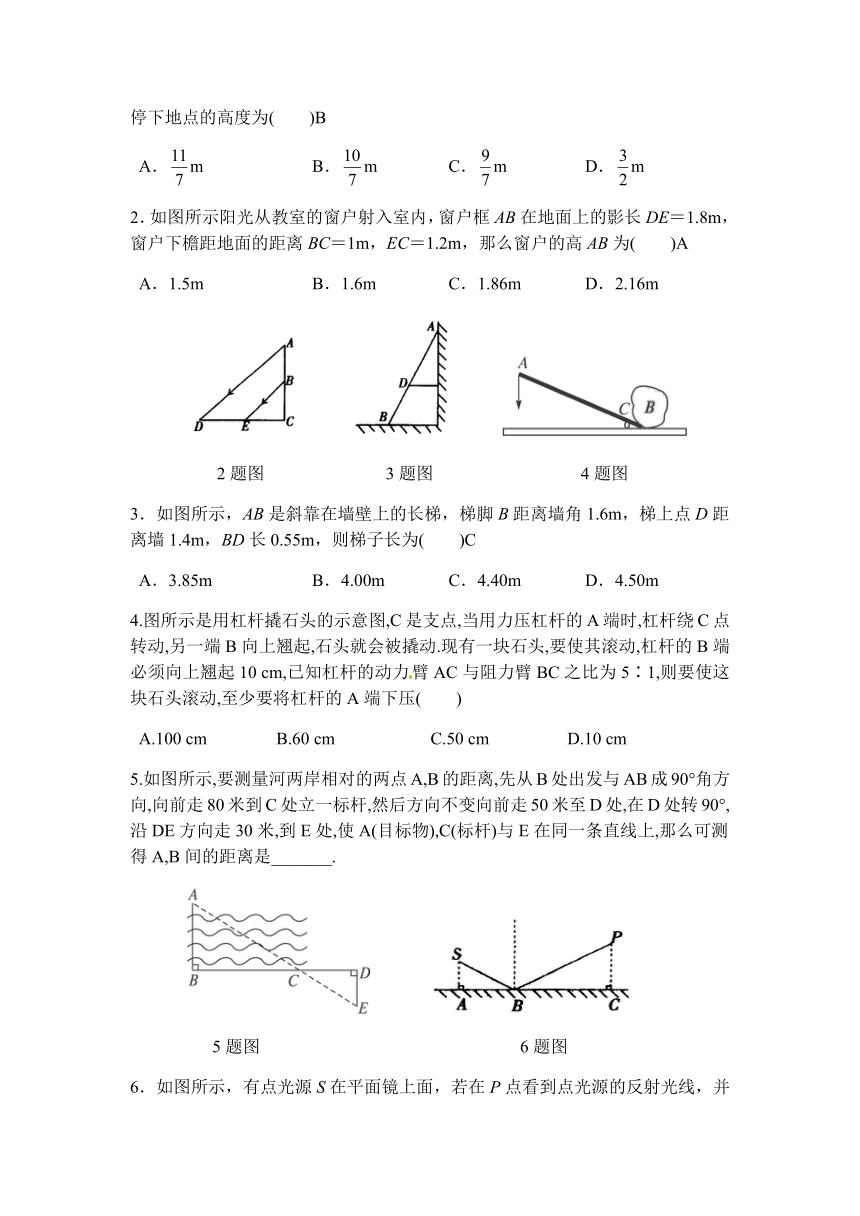
2.如图,DE⊥EB,AB⊥EB,∠DCE=∠ACB,DE=12 m,EC=15 m,BC=30 m,
则AB= m.
2题图 4题图
3.已知A、B两地相距300 km,在地图上量得两地相距15 cm,则图上距离与实际距离之比为___________.
4.某一时刻,测得旗杆的影长为8 m,李明测得小芳的影长为1 m,已知小芳的身高为1.5 m,则旗杆的高度是_______________m.
5.马戏团让狮子和公鸡表演跷跷板节目,跷跷板支柱AB的高度为1.2米,若吊环高度为2米,支点A为跷跷板PQ的中点,狮子能否将公鸡送到吊环上?为什么?
5题图
互动训练
知识点一:相似三角形判定及性质的实际应用
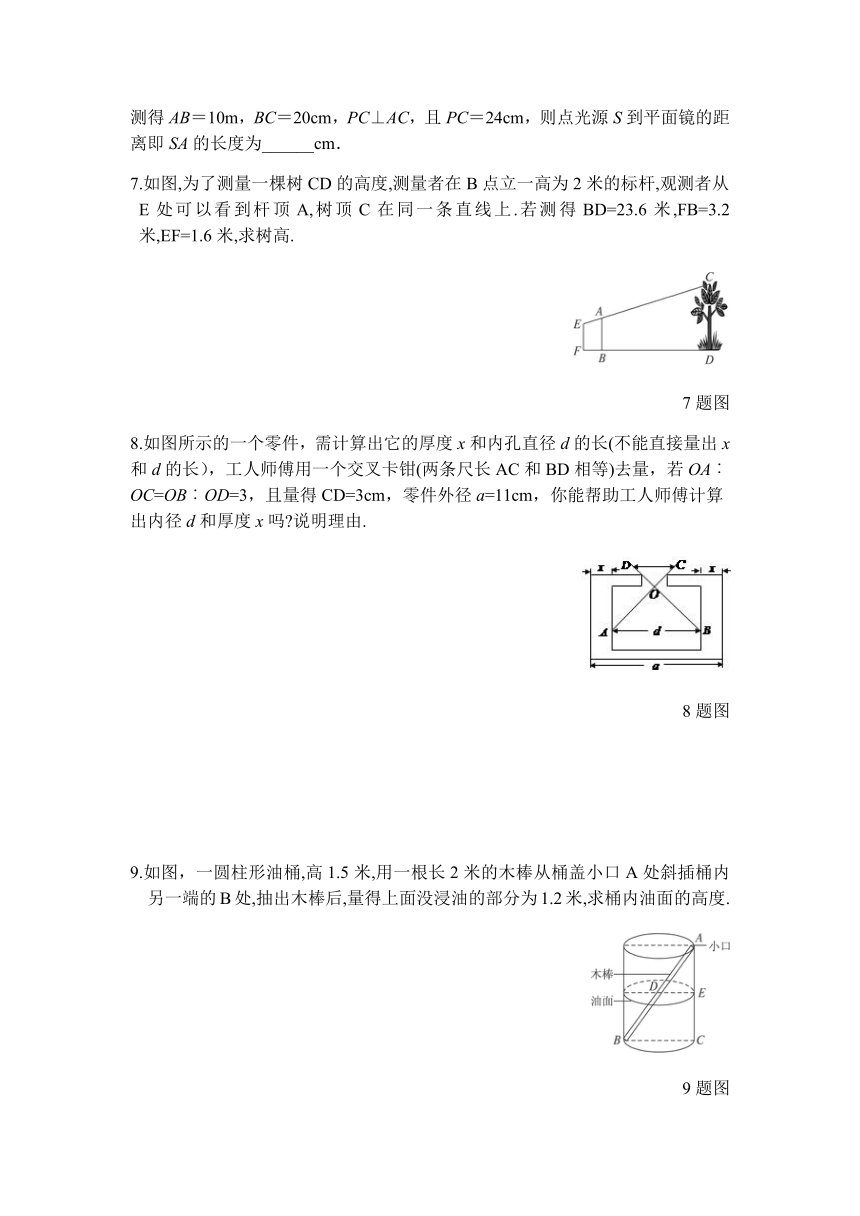
1.一斜坡长70m,它的高为5m,将某物从斜坡起点推到坡上20m处停止下,停下地点的高度为( )B
A.false B.false C.false D.false
2.如图所示阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐距地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )A
A.1.5m B.1.6m C.1.86m D.2.16m
2题图 3题图 4题图
3.如图所示,AB是斜靠在墙壁上的长梯,梯脚B距离墙角1.6m,梯上点D距离墙1.4m,BD长0.55m,则梯子长为( )C
A.3.85m B.4.00m C.4.40m D.4.50m
4.图所示是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就会被撬动.现有一块石头,要使其滚动,杠杆的B端必须向上翘起10 cm,已知杠杆的动力臂AC与阻力臂BC之比为5∶1,则要使这块石头滚动,至少要将杠杆的A端下压( )
A.100 cm B.60 cm C.50 cm D.10 cm
5.如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是_______.
5题图 6题图
6.如图所示,有点光源S在平面镜上面,若在P点看到点光源的反射光线,并测得AB=10m,BC=20cm,PC⊥AC,且PC=24cm,则点光源S到平面镜的距离即SA的长度为______cm.
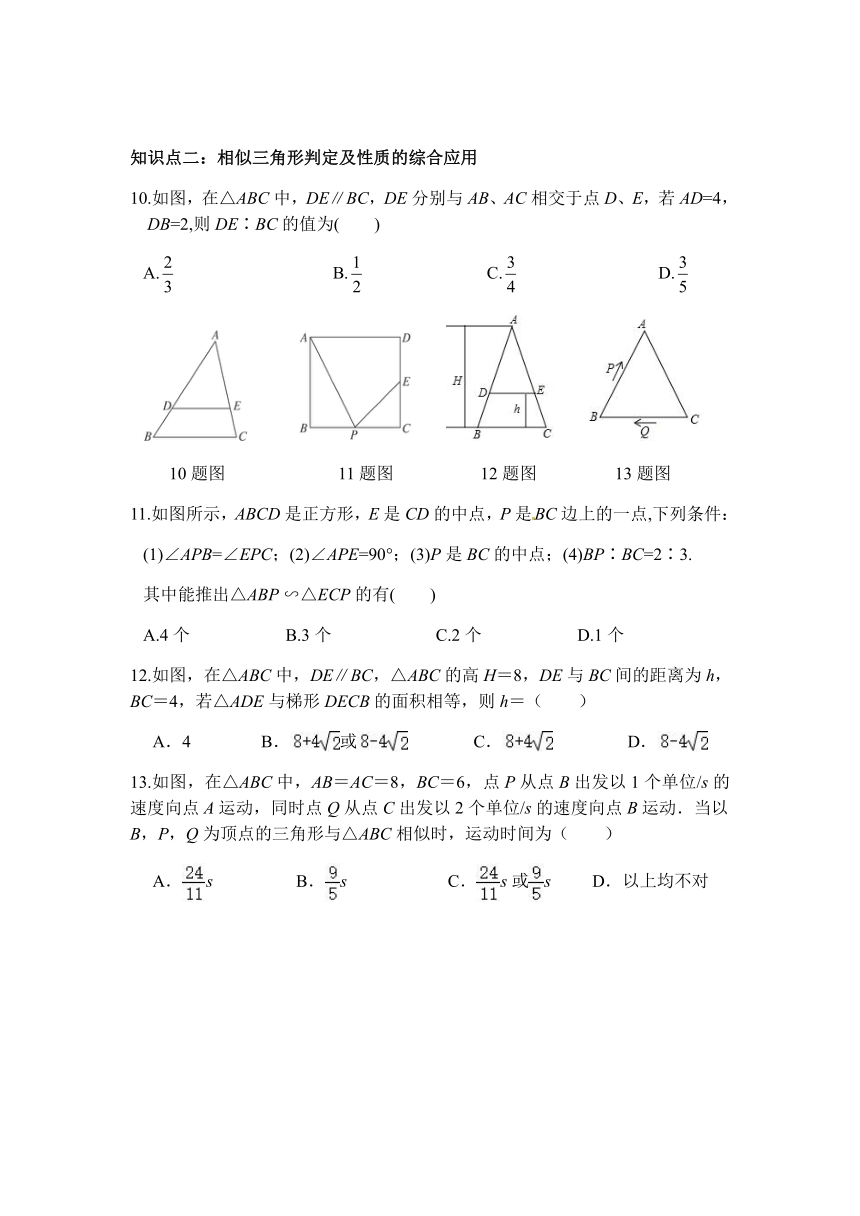
7.如图,为了测量一棵树CD的高度,测量者在B点立一高为2米的标杆,观测者从E处可以看到杆顶A,树顶C在同一条直线上.若测得BD=23.6米,FB=3.2米,EF=1.6米,求树高.
7题图
8.如图所示的一个零件,需计算出它的厚度x和内孔直径d的长(不能直接量出x和d的长),工人师傅用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA︰OC=OB︰OD=3,且量得CD=3cm,零件外径a=11cm,你能帮助工人师傅计算出内径d和厚度x吗?说明理由.
8题图
9.如图,一圆柱形油桶,高1.5米,用一根长2米的木棒从桶盖小口A处斜插桶内另一端的B处,抽出木棒后,量得上面没浸油的部分为1.2米,求桶内油面的高度.
9题图
知识点二:相似三角形判定及性质的综合应用
10.如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则DE∶BC的值为( )
A.false B.false C.false D.false
10题图 11题图 12题图 13题图
11.如图所示,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:
(1)∠APB=∠EPC;(2)∠APE=90°;(3)P是BC的中点;(4)BP∶BC=2∶3.
其中能推出△ABP ∽△ECP的有( )
A.4个 B.3个 C.2个 D.1个
12.如图,在△ABC中,DE∥BC,△ABC的高H=8,DE与BC间的距离为h,BC=4,若△ADE与梯形DECB的面积相等,则h=( )
A.4 B.或 C. D.
13.如图,在△ABC中,AB=AC=8,BC=6,点P从点B出发以1个单位/s的速度向点A运动,同时点Q从点C出发以2个单位/s的速度向点B运动.当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为( )
A.s B.s C.s或s D.以上均不对
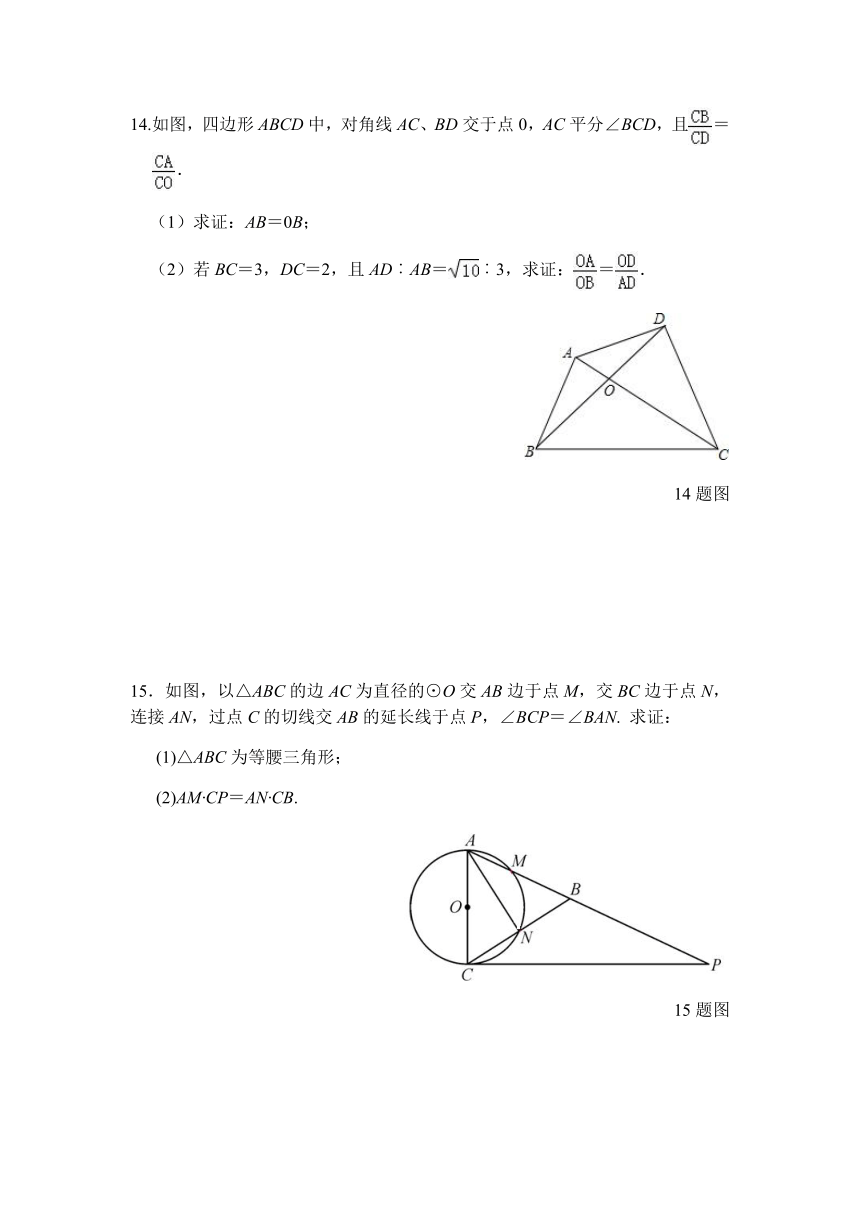
14.如图,四边形ABCD中,对角线AC、BD交于点0,AC平分∠BCD,且=.
(1)求证:AB=0B;
(2)若BC=3,DC=2,且AD︰AB=︰3,求证:=.
14题图
15.如图,以△ABC的边AC为直径的⊙O交AB边于点M,交BC边于点N,连接AN,过点C的切线交AB的延长线于点P,∠BCP=∠BAN. 求证:
(1)△ABC为等腰三角形;
(2)AM·CP=AN·CB.
15题图
课时达标
1.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为( )
A.15cm B.20cm C.25cm D.30cm
1题图 2题图 3题图
2.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=5 m,点P到CD的距离是3 m,则P到AB的距离是( )
A.false m B.false m C.false m D.false m
3.如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )
A.40m B.60m C.120m D.180m
4.如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( )
A.变长了1.5米 B.变短了2.5米
C.变长了3.5米 D.变短了3.5米
4题图 5题图 6题图
5.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么AC为 米.
6.如图,已知小华、小强的身高分别为1.8m,1.5m,路灯的高度为3.6m.小华、小强在同一盏路灯下的影长分别为2.3m,2m、则小华、小强之间的水平距离为 .
7.如图,BE⊥AC于B,CD⊥AC于C,AE∥BD,若BE=1.7米,AB=3米,BC=12米,求CD的长.
7题图
8.如图,射击瞄准时,要求枪的标尺缺口上沿中央A,准星尖B和瞄准点C在一条直线上,这样才能命中目标. 已知某种冲锋枪基线AB长38.5 cm,如果射击距离AC=
100 m,当准星尖在缺口内偏差BB′为1 mm时,弹着偏差CC′是多少?(BB′∥CC′)
8题图
9.如图,AB是斜靠在墙壁上的长梯,梯脚B距墙80 cm,梯上点D距墙70 cm,BD长55 cm,求梯子的长.
9题图
10.一条河的两岸有一段是平行的,在河的这岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这一岸离开岸边25米处看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树, 求河宽.
10题图
11.一位同学想利用树影测量树高AB,他在某一时刻测得小树高为1米,树影长0.9米,但当他马上测量树影时,因树靠近建筑物,影子不全落在地上,有一部分落在墙上,如图,他先测得地面部分的影子长2.7米,又测得墙上的影高CD为1.2米,试问树有多高?
11题图
12.如图所示,大江的一侧有甲,乙两个工厂,它们有垂直于江边的小路,长度分别为m千米及n千米,设两条小路相距l千米.现在要在江边建立一个抽水站,把水送到甲,乙两厂去,欲使供水管路最短,抽水站应建在哪里?
12题图
13.如图,一人拿着一个刻有厘米分度的小尺,站在距离电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上的12个分度恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.
13题图
14.某同学想用镜子测量一棵古松树的高,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图,第一次他把镜子放在C点,人在F点正好看到树尖A;第二次他把镜子放在C′处,人在F′处正好看到树尖A,已知某同学的眼睛距地面1.70 m,量得CC′为12 m,CF长1.8 m,C′F′为3.84 m,求这棵古松树的高.
14题图
15.小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1)小明距离路灯多远?
(2)求路灯高度.
15题图
16.如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
16题图
拓展探究
1.如图,AB⊥BD,CD⊥BD,AB=3,CD=8,BD=10,一动点P从点B向右D运动,问当点P离点B多远时,△PAB与△PCD是相似三角形?
1题图
2.已知:如图,梯形ABCD中,AB∥DC,∠B=90°,AB=3,BC=11,DC=6.请问:在BC上若存在点P,使得△ABP与△PCD相似,求BP的长及它们的面积比.
2题图
3.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”
27.2.3相似三角形的应用举例答案
自主预习
1. B. 解析:因太阳光线是平行的,所以同时同地光线,物高,影长组成的三角形都相似. 答案:B.
2. 24. 解析:∵△ABC∽△DEC,∴AB=24. 答案:24.
3. 1∶2 000 000. 解析:AB=300 km=30 000 000 cm,
所以图上距离∶实际距离=1∶2 000 000. 答案:1∶2 000 000.
4. 解:如图所示,∵△ABC∽△DEF,
∴false. ∴DF=12 m. 答案:12.
5.解:狮子能将公鸡送到吊环上.
理由:过点Q作QH⊥PC于点H,即狮子将跷跷板P端按到底时可得到Rt△PHQ,
∵AB∥QH,∴△PAB∽△PQH,∴false.
∵A为PQ的中点, ∴PQ=2PA,
∴QH=2AB=2.4>2.
∴狮子能将公鸡送到吊环上
互动训练
1.B. 2.A. 3.C.
4. C. 解析:杠杆运动过程中构成的三角形相似.答案:C
5. 48米. 解析:因为△ABC∽△EDC,所以false.答案:48米
6. 12.
7. 解:由题意得△AEM∽△CEN,
∴false.而AM=0.4,EM=3.2,EN=26.8,
∴CN=3.35. ∴CD=4.95(米).
答:树高4.95米.
7题图 9题图
8. 解:∵OA︰OC=OB︰OD=3 , ∠AOB=∠COD.
∴△AOB∽△COD.
∴false 即false,∴d=9.
∴false
∴d=9cm, x=1cm.
9. 解:根据题意建立数学模型,如图,
AD=1.2米,AB=2米,AC=1.5米, DE∥BC.
∵DE∥BC, ∴∠ADE=∠B,∠AED=∠C.
∴△ADE∽△ABC.
∴false.∴false
∴AE=0.9(米).
∴EC=AC-AE=1.5-0.9=0.6(米).
10. A. 解析:因△ADE∽△ABC,故false.答案:A
11. C. 解析:(1)中因为∠B=∠C,∠APB=∠EPC,所以△ABP∽△ECP;
(4)中因为BP∶BC=2∶3, 所以BP=falseBC,PC=falseBC.所以false=2,
且∠B=∠C=90°. 所以△ABP∽△ECP.故选C. 答案:C.
12. D. 解析:∵△ADE与梯形DECB的面积相等,∴,
∵△ABC中,DE∥BC,∴△ADE∽△ABC,∴.
如图,过点A作AN⊥BC交DE于点M,
∵AN=8,∴AM=8﹣h,∴,∴h=8﹣4.故选:D.
12题图 14题图
13. C. 解析:设运动时间为t秒.BP=t,CQ=2t,BQ=BC﹣CQ=6﹣2t,
当△BAC∽△BPQ,=,即=,解得t=;
当△BCA∽△BPQ,=,即=,解得t=,
综上所述,当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为s或s,
故选:C.
14.证明:(1)∵AC平分∠BCD,∴∠BCA=∠DCA,
∵=,∴△ABC∽△ODC,∴∠DOC=∠BAC,
∵∠AOB=∠DOC,∴∠BAO=∠BOA,∴AB=OB;
(2)∵△ABC∽△ODC,
∴, ∴AB=OD,AC=OC,∴AO=OC,
设AD=x,则AB=OB=3x,OD=2x,
过A作AH⊥BD,设OH=a,
由勾股定理得AB2﹣BH2=AD2﹣DH2,
即(3x)2﹣(3x﹣a)2=(x)2﹣(2x+a)2,
解得:a=x,∴BH=x,
∴AH=,∴AO==x,
∴==,=,∴=.
15. 证明:(1)∵AC为⊙O的直径,∴∠ANC=90°.
∵PC是⊙O的切线,∴∠BCP=∠CAN.
∵∠BCP=∠BAN,∴∠BAN=∠CAN.
又∵AN⊥BC,∴AB=AC.∴△ABC为等腰三角形.
(2)连接MN∵△ABC为等腰三角形,AB=AC,
∴∠ABC=∠ACB.
∵∠PBC+∠ABC=∠AMN+∠ACN=180°,
∴∠PBC=∠AMN.
由(1)知∠BCP=∠BAN,∴△BPC∽△MNA.
∴=,即AM·CP=AN·CB.
15题图
课时达标
1. D. 解析:∵AB∥DE,∴△CAB∽△CDE,∴=,而BC=BE,
∴DE=2AB=2×15=30(cm).故选:D.
2. C. 解析:设P到AB的距离为x米,则有false.x=1.2(m). 故选:C.
3. C. 解析:∵RQ⊥PS,TS⊥PS,∴RQ∥TS,∴△PQR∽△PST,
∴=,即=,∴PQ=120(m).故选:C.
4. D. 解析:设小明在A处时影长为x,B处时影长为y.
∵AD∥OP,BC∥OP,
∴△ADM∽△OPM,△BCN∽△OPN,
∴ADOP=MAMO,BCOP=BNON,则xx+20=1.68,∴x=5;
yy+20-14=1.68,∴y=1.5,∴x﹣y=3.5,
故变短了3.5米.故选:D.
4题图 6题图
5. 7.解析:∵BD⊥AB,AC⊥AB,∴BD∥AC,
∴△ACE∽△BDE,
∴ACBD=AEBE,∴AC1=1.40.2,∴AC=7(米),故答案为:7.
6. 5.1m. 解析:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴CDAB=DEBE,FNFB=MNAB,
由题意得:DE=2.3,CD=1.8,FN=2,MN=1.5,AB=3.6,
即1.83.6=2.3BE,2FB=1.53.6,
解得:BE=4.6m,BF=245,
∴BD=BE﹣DE=2.3,BN=BF﹣FN=145=2.8,
∴DN=5.1(m),
答:小华、小强之间的水平距离为5.1m,故答案为:5.1m.
7. 解:∵BE⊥AC于B,CD⊥AC于C,
∴∠ABE=∠BCD=90°.∵AE∥BD,∴∠A=∠CBD.
∴△ABE∽△BCD.∴false,
即false.∴CD=6.8(米).
∴CD的长为6.8米.
8. 解:∵BB′∥CC′,∴△ABB′∽△ACC′.
∴false.∴CC′=false(m).
即弹着偏差false m.
9. 解:设梯子长为x cm, ∵△ADE∽△ABF,
∴false. 则有false, 解得x=440.
经检验x=440为所列方程的根,所以梯长为440 cm.
10. 解:根据题意,画出图形如图,其中AB=50米,CD=5×4=20米,GE⊥CD,GF⊥AB,点G、E、F共线,GE=25米.
∵AB∥CD, ∴∠DCG=∠BAG,∠CDG=∠ABG.
∴△GCD∽△GAB.
又∵GE⊥CD,GF⊥AB,
∴false(相似三角形对应高的比等于相似比).
∴GF=false=62.5(米).
∴河宽EF=GF-GE=62.5-25=37.5(米).
10题图 11题图
11. 解法一:如图,延长AD,BE相交于点C,则CE就是树影长的一部分,
false,即false.∴CE=1.08 (m).
∴BC=BE+EC=2.7+1.08=3.78 (m).
∴false,即false.
∴AB=4.2 (m).
解法二:过E作EF∥AD交AB于F.
false,即false. ∴BF=3 m.
AB=AF+BF=3+1.2=4.2 (m)
12. 解:如图所示,AD垂直于江边于D,BE垂直于江边于E,
则AD=m千米,BE=n千米,DE=l千米. 延长BE至F,使EF=BE.
连结AF交DE于C,则在C点建抽水站,到甲、乙两厂的供水管路AC+CB为最短.
设CD=x千米,因为Rt△ADC∽Rt△FEC,
所以false, 即false, 解得x=false(米).
12题图
13. 解:设电线杆高x m,因为两三角形相似,
则有false,
解得x=6,经检验x=6为原分式方程的根,
所以电线杆高6 m.
14. 解:设BC=y m,AB=x m,作CM⊥BF,C′M′⊥BF′.
由物理学中光的反射定理,得∠ACM=∠ECM,∠AC′M′=∠E′C′M′,
所以∠ACB=∠ECF,∠AC′B=∠E′C′F′.
因为 ∠ABC=∠EFC=90°,∠ABC=∠E′F′C′=90°,
所以△ABC∽△EFC,△ABC′∽△E′F′C′.所以false.
所以false,① false.②
解①②组成的方程组,得false
所以这棵古松树的高为10米.
15.解:(1)设DB=xm,
∵AB∥CD,∴∠QBA=∠QDC,∠QAB=∠QCD,
∴△QAB∽△QCD,ABCD=BQQD,
同理可得:ABEF=BPPF,
∵CD=EF,∴BQDQ=BPPF,
∴4x+4=55+27-x, ∴x=12,
即小明距离路灯12m.
(2)由ABCD=BQQD得1.5DC=412+4,∴CD=6
即路灯高6m.
16. (1)证明:∵∠EFG=∠DFG,
∴∠EFB=∠DFC,又∵∠B=∠C,
∴△BEF∽△CDF;
(2)解:∵△BEF∽△CDF,∴=,
设FC=xcm,则=,解得:x=160,
答:CF的长为160cm.
拓展探究
1.解:∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°,
∴当或=时,△PAB与△PCD是相似三角形,
∵AB=3,CD=8,BD=10,
∴=或=,∴BP=6或4或,
即PB=6或4或,时,△PAB与△PCD是相似三角形.
2.答案:当BP=2时,S△ABP∶S△PCD=1∶9;
当false时,S△ABP∶S△DCP=1∶4;
当BP=9时,S△ABP:S△PCD=9∶4.
3. 解:如图1,∵四边形CDEF是正方形,∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=12﹣x,
∵DE∥CF,∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴DEBC=ADAC,∴x5=12-x12,x=6017,
如图2,四边形DGFE是正方形,
过C作CP⊥AB于P,交DG于Q,
设ED=x,S△ABC=12AC?BC=12AB?CP,
12×5=13CP,CP=6013,
同理得:△CDG∽△CAB,
∴DGAB=CQCP,∴x13=6013-x6013,x=780229<6017,
∴该直角三角形能容纳的正方形边长最大是6017(步).
自主预习
1.在同一时刻同一个地点物体的高度与自身的影长的关系是( )
A.成反比例 B.成正比例 C.相等 D.不成比例
2.如图,DE⊥EB,AB⊥EB,∠DCE=∠ACB,DE=12 m,EC=15 m,BC=30 m,
则AB= m.
2题图 4题图
3.已知A、B两地相距300 km,在地图上量得两地相距15 cm,则图上距离与实际距离之比为___________.
4.某一时刻,测得旗杆的影长为8 m,李明测得小芳的影长为1 m,已知小芳的身高为1.5 m,则旗杆的高度是_______________m.
5.马戏团让狮子和公鸡表演跷跷板节目,跷跷板支柱AB的高度为1.2米,若吊环高度为2米,支点A为跷跷板PQ的中点,狮子能否将公鸡送到吊环上?为什么?
5题图
互动训练
知识点一:相似三角形判定及性质的实际应用
1.一斜坡长70m,它的高为5m,将某物从斜坡起点推到坡上20m处停止下,停下地点的高度为( )B
A.false B.false C.false D.false
2.如图所示阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐距地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )A
A.1.5m B.1.6m C.1.86m D.2.16m
2题图 3题图 4题图
3.如图所示,AB是斜靠在墙壁上的长梯,梯脚B距离墙角1.6m,梯上点D距离墙1.4m,BD长0.55m,则梯子长为( )C
A.3.85m B.4.00m C.4.40m D.4.50m
4.图所示是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就会被撬动.现有一块石头,要使其滚动,杠杆的B端必须向上翘起10 cm,已知杠杆的动力臂AC与阻力臂BC之比为5∶1,则要使这块石头滚动,至少要将杠杆的A端下压( )
A.100 cm B.60 cm C.50 cm D.10 cm
5.如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是_______.
5题图 6题图
6.如图所示,有点光源S在平面镜上面,若在P点看到点光源的反射光线,并测得AB=10m,BC=20cm,PC⊥AC,且PC=24cm,则点光源S到平面镜的距离即SA的长度为______cm.
7.如图,为了测量一棵树CD的高度,测量者在B点立一高为2米的标杆,观测者从E处可以看到杆顶A,树顶C在同一条直线上.若测得BD=23.6米,FB=3.2米,EF=1.6米,求树高.
7题图
8.如图所示的一个零件,需计算出它的厚度x和内孔直径d的长(不能直接量出x和d的长),工人师傅用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA︰OC=OB︰OD=3,且量得CD=3cm,零件外径a=11cm,你能帮助工人师傅计算出内径d和厚度x吗?说明理由.
8题图
9.如图,一圆柱形油桶,高1.5米,用一根长2米的木棒从桶盖小口A处斜插桶内另一端的B处,抽出木棒后,量得上面没浸油的部分为1.2米,求桶内油面的高度.
9题图
知识点二:相似三角形判定及性质的综合应用
10.如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则DE∶BC的值为( )
A.false B.false C.false D.false
10题图 11题图 12题图 13题图
11.如图所示,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:
(1)∠APB=∠EPC;(2)∠APE=90°;(3)P是BC的中点;(4)BP∶BC=2∶3.
其中能推出△ABP ∽△ECP的有( )
A.4个 B.3个 C.2个 D.1个
12.如图,在△ABC中,DE∥BC,△ABC的高H=8,DE与BC间的距离为h,BC=4,若△ADE与梯形DECB的面积相等,则h=( )
A.4 B.或 C. D.
13.如图,在△ABC中,AB=AC=8,BC=6,点P从点B出发以1个单位/s的速度向点A运动,同时点Q从点C出发以2个单位/s的速度向点B运动.当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为( )
A.s B.s C.s或s D.以上均不对
14.如图,四边形ABCD中,对角线AC、BD交于点0,AC平分∠BCD,且=.
(1)求证:AB=0B;
(2)若BC=3,DC=2,且AD︰AB=︰3,求证:=.
14题图
15.如图,以△ABC的边AC为直径的⊙O交AB边于点M,交BC边于点N,连接AN,过点C的切线交AB的延长线于点P,∠BCP=∠BAN. 求证:
(1)△ABC为等腰三角形;
(2)AM·CP=AN·CB.
15题图
课时达标
1.如图,小明在打乒乓球时,为使球恰好能过网(设网高AB=15cm),且落在对方区域桌子底线C处,已知小明在自己桌子底线上方击球,则他击球点距离桌面的高度DE为( )
A.15cm B.20cm C.25cm D.30cm
1题图 2题图 3题图
2.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=5 m,点P到CD的距离是3 m,则P到AB的距离是( )
A.false m B.false m C.false m D.false m
3.如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )
A.40m B.60m C.120m D.180m
4.如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( )
A.变长了1.5米 B.变短了2.5米
C.变长了3.5米 D.变短了3.5米
4题图 5题图 6题图
5.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么AC为 米.
6.如图,已知小华、小强的身高分别为1.8m,1.5m,路灯的高度为3.6m.小华、小强在同一盏路灯下的影长分别为2.3m,2m、则小华、小强之间的水平距离为 .
7.如图,BE⊥AC于B,CD⊥AC于C,AE∥BD,若BE=1.7米,AB=3米,BC=12米,求CD的长.
7题图
8.如图,射击瞄准时,要求枪的标尺缺口上沿中央A,准星尖B和瞄准点C在一条直线上,这样才能命中目标. 已知某种冲锋枪基线AB长38.5 cm,如果射击距离AC=
100 m,当准星尖在缺口内偏差BB′为1 mm时,弹着偏差CC′是多少?(BB′∥CC′)
8题图
9.如图,AB是斜靠在墙壁上的长梯,梯脚B距墙80 cm,梯上点D距墙70 cm,BD长55 cm,求梯子的长.
9题图
10.一条河的两岸有一段是平行的,在河的这岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这一岸离开岸边25米处看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树, 求河宽.
10题图
11.一位同学想利用树影测量树高AB,他在某一时刻测得小树高为1米,树影长0.9米,但当他马上测量树影时,因树靠近建筑物,影子不全落在地上,有一部分落在墙上,如图,他先测得地面部分的影子长2.7米,又测得墙上的影高CD为1.2米,试问树有多高?
11题图
12.如图所示,大江的一侧有甲,乙两个工厂,它们有垂直于江边的小路,长度分别为m千米及n千米,设两条小路相距l千米.现在要在江边建立一个抽水站,把水送到甲,乙两厂去,欲使供水管路最短,抽水站应建在哪里?
12题图
13.如图,一人拿着一个刻有厘米分度的小尺,站在距离电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上的12个分度恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.
13题图
14.某同学想用镜子测量一棵古松树的高,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图,第一次他把镜子放在C点,人在F点正好看到树尖A;第二次他把镜子放在C′处,人在F′处正好看到树尖A,已知某同学的眼睛距地面1.70 m,量得CC′为12 m,CF长1.8 m,C′F′为3.84 m,求这棵古松树的高.
14题图
15.小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1)小明距离路灯多远?
(2)求路灯高度.
15题图
16.如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
16题图
拓展探究
1.如图,AB⊥BD,CD⊥BD,AB=3,CD=8,BD=10,一动点P从点B向右D运动,问当点P离点B多远时,△PAB与△PCD是相似三角形?
1题图
2.已知:如图,梯形ABCD中,AB∥DC,∠B=90°,AB=3,BC=11,DC=6.请问:在BC上若存在点P,使得△ABP与△PCD相似,求BP的长及它们的面积比.
2题图
3.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”
27.2.3相似三角形的应用举例答案
自主预习
1. B. 解析:因太阳光线是平行的,所以同时同地光线,物高,影长组成的三角形都相似. 答案:B.
2. 24. 解析:∵△ABC∽△DEC,∴AB=24. 答案:24.
3. 1∶2 000 000. 解析:AB=300 km=30 000 000 cm,
所以图上距离∶实际距离=1∶2 000 000. 答案:1∶2 000 000.
4. 解:如图所示,∵△ABC∽△DEF,
∴false. ∴DF=12 m. 答案:12.
5.解:狮子能将公鸡送到吊环上.
理由:过点Q作QH⊥PC于点H,即狮子将跷跷板P端按到底时可得到Rt△PHQ,
∵AB∥QH,∴△PAB∽△PQH,∴false.
∵A为PQ的中点, ∴PQ=2PA,
∴QH=2AB=2.4>2.
∴狮子能将公鸡送到吊环上
互动训练
1.B. 2.A. 3.C.
4. C. 解析:杠杆运动过程中构成的三角形相似.答案:C
5. 48米. 解析:因为△ABC∽△EDC,所以false.答案:48米
6. 12.
7. 解:由题意得△AEM∽△CEN,
∴false.而AM=0.4,EM=3.2,EN=26.8,
∴CN=3.35. ∴CD=4.95(米).
答:树高4.95米.
7题图 9题图
8. 解:∵OA︰OC=OB︰OD=3 , ∠AOB=∠COD.
∴△AOB∽△COD.
∴false 即false,∴d=9.
∴false
∴d=9cm, x=1cm.
9. 解:根据题意建立数学模型,如图,
AD=1.2米,AB=2米,AC=1.5米, DE∥BC.
∵DE∥BC, ∴∠ADE=∠B,∠AED=∠C.
∴△ADE∽△ABC.
∴false.∴false
∴AE=0.9(米).
∴EC=AC-AE=1.5-0.9=0.6(米).
10. A. 解析:因△ADE∽△ABC,故false.答案:A
11. C. 解析:(1)中因为∠B=∠C,∠APB=∠EPC,所以△ABP∽△ECP;
(4)中因为BP∶BC=2∶3, 所以BP=falseBC,PC=falseBC.所以false=2,
且∠B=∠C=90°. 所以△ABP∽△ECP.故选C. 答案:C.
12. D. 解析:∵△ADE与梯形DECB的面积相等,∴,
∵△ABC中,DE∥BC,∴△ADE∽△ABC,∴.
如图,过点A作AN⊥BC交DE于点M,
∵AN=8,∴AM=8﹣h,∴,∴h=8﹣4.故选:D.
12题图 14题图
13. C. 解析:设运动时间为t秒.BP=t,CQ=2t,BQ=BC﹣CQ=6﹣2t,
当△BAC∽△BPQ,=,即=,解得t=;
当△BCA∽△BPQ,=,即=,解得t=,
综上所述,当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为s或s,
故选:C.
14.证明:(1)∵AC平分∠BCD,∴∠BCA=∠DCA,
∵=,∴△ABC∽△ODC,∴∠DOC=∠BAC,
∵∠AOB=∠DOC,∴∠BAO=∠BOA,∴AB=OB;
(2)∵△ABC∽△ODC,
∴, ∴AB=OD,AC=OC,∴AO=OC,
设AD=x,则AB=OB=3x,OD=2x,
过A作AH⊥BD,设OH=a,
由勾股定理得AB2﹣BH2=AD2﹣DH2,
即(3x)2﹣(3x﹣a)2=(x)2﹣(2x+a)2,
解得:a=x,∴BH=x,
∴AH=,∴AO==x,
∴==,=,∴=.
15. 证明:(1)∵AC为⊙O的直径,∴∠ANC=90°.
∵PC是⊙O的切线,∴∠BCP=∠CAN.
∵∠BCP=∠BAN,∴∠BAN=∠CAN.
又∵AN⊥BC,∴AB=AC.∴△ABC为等腰三角形.
(2)连接MN∵△ABC为等腰三角形,AB=AC,
∴∠ABC=∠ACB.
∵∠PBC+∠ABC=∠AMN+∠ACN=180°,
∴∠PBC=∠AMN.
由(1)知∠BCP=∠BAN,∴△BPC∽△MNA.
∴=,即AM·CP=AN·CB.
15题图
课时达标
1. D. 解析:∵AB∥DE,∴△CAB∽△CDE,∴=,而BC=BE,
∴DE=2AB=2×15=30(cm).故选:D.
2. C. 解析:设P到AB的距离为x米,则有false.x=1.2(m). 故选:C.
3. C. 解析:∵RQ⊥PS,TS⊥PS,∴RQ∥TS,∴△PQR∽△PST,
∴=,即=,∴PQ=120(m).故选:C.
4. D. 解析:设小明在A处时影长为x,B处时影长为y.
∵AD∥OP,BC∥OP,
∴△ADM∽△OPM,△BCN∽△OPN,
∴ADOP=MAMO,BCOP=BNON,则xx+20=1.68,∴x=5;
yy+20-14=1.68,∴y=1.5,∴x﹣y=3.5,
故变短了3.5米.故选:D.
4题图 6题图
5. 7.解析:∵BD⊥AB,AC⊥AB,∴BD∥AC,
∴△ACE∽△BDE,
∴ACBD=AEBE,∴AC1=1.40.2,∴AC=7(米),故答案为:7.
6. 5.1m. 解析:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴CDAB=DEBE,FNFB=MNAB,
由题意得:DE=2.3,CD=1.8,FN=2,MN=1.5,AB=3.6,
即1.83.6=2.3BE,2FB=1.53.6,
解得:BE=4.6m,BF=245,
∴BD=BE﹣DE=2.3,BN=BF﹣FN=145=2.8,
∴DN=5.1(m),
答:小华、小强之间的水平距离为5.1m,故答案为:5.1m.
7. 解:∵BE⊥AC于B,CD⊥AC于C,
∴∠ABE=∠BCD=90°.∵AE∥BD,∴∠A=∠CBD.
∴△ABE∽△BCD.∴false,
即false.∴CD=6.8(米).
∴CD的长为6.8米.
8. 解:∵BB′∥CC′,∴△ABB′∽△ACC′.
∴false.∴CC′=false(m).
即弹着偏差false m.
9. 解:设梯子长为x cm, ∵△ADE∽△ABF,
∴false. 则有false, 解得x=440.
经检验x=440为所列方程的根,所以梯长为440 cm.
10. 解:根据题意,画出图形如图,其中AB=50米,CD=5×4=20米,GE⊥CD,GF⊥AB,点G、E、F共线,GE=25米.
∵AB∥CD, ∴∠DCG=∠BAG,∠CDG=∠ABG.
∴△GCD∽△GAB.
又∵GE⊥CD,GF⊥AB,
∴false(相似三角形对应高的比等于相似比).
∴GF=false=62.5(米).
∴河宽EF=GF-GE=62.5-25=37.5(米).
10题图 11题图
11. 解法一:如图,延长AD,BE相交于点C,则CE就是树影长的一部分,
false,即false.∴CE=1.08 (m).
∴BC=BE+EC=2.7+1.08=3.78 (m).
∴false,即false.
∴AB=4.2 (m).
解法二:过E作EF∥AD交AB于F.
false,即false. ∴BF=3 m.
AB=AF+BF=3+1.2=4.2 (m)
12. 解:如图所示,AD垂直于江边于D,BE垂直于江边于E,
则AD=m千米,BE=n千米,DE=l千米. 延长BE至F,使EF=BE.
连结AF交DE于C,则在C点建抽水站,到甲、乙两厂的供水管路AC+CB为最短.
设CD=x千米,因为Rt△ADC∽Rt△FEC,
所以false, 即false, 解得x=false(米).
12题图
13. 解:设电线杆高x m,因为两三角形相似,
则有false,
解得x=6,经检验x=6为原分式方程的根,
所以电线杆高6 m.
14. 解:设BC=y m,AB=x m,作CM⊥BF,C′M′⊥BF′.
由物理学中光的反射定理,得∠ACM=∠ECM,∠AC′M′=∠E′C′M′,
所以∠ACB=∠ECF,∠AC′B=∠E′C′F′.
因为 ∠ABC=∠EFC=90°,∠ABC=∠E′F′C′=90°,
所以△ABC∽△EFC,△ABC′∽△E′F′C′.所以false.
所以false,① false.②
解①②组成的方程组,得false
所以这棵古松树的高为10米.
15.解:(1)设DB=xm,
∵AB∥CD,∴∠QBA=∠QDC,∠QAB=∠QCD,
∴△QAB∽△QCD,ABCD=BQQD,
同理可得:ABEF=BPPF,
∵CD=EF,∴BQDQ=BPPF,
∴4x+4=55+27-x, ∴x=12,
即小明距离路灯12m.
(2)由ABCD=BQQD得1.5DC=412+4,∴CD=6
即路灯高6m.
16. (1)证明:∵∠EFG=∠DFG,
∴∠EFB=∠DFC,又∵∠B=∠C,
∴△BEF∽△CDF;
(2)解:∵△BEF∽△CDF,∴=,
设FC=xcm,则=,解得:x=160,
答:CF的长为160cm.
拓展探究
1.解:∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°,
∴当或=时,△PAB与△PCD是相似三角形,
∵AB=3,CD=8,BD=10,
∴=或=,∴BP=6或4或,
即PB=6或4或,时,△PAB与△PCD是相似三角形.
2.答案:当BP=2时,S△ABP∶S△PCD=1∶9;
当false时,S△ABP∶S△DCP=1∶4;
当BP=9时,S△ABP:S△PCD=9∶4.
3. 解:如图1,∵四边形CDEF是正方形,∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=12﹣x,
∵DE∥CF,∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴DEBC=ADAC,∴x5=12-x12,x=6017,
如图2,四边形DGFE是正方形,
过C作CP⊥AB于P,交DG于Q,
设ED=x,S△ABC=12AC?BC=12AB?CP,
12×5=13CP,CP=6013,
同理得:△CDG∽△CAB,
∴DGAB=CQCP,∴x13=6013-x6013,x=780229<6017,
∴该直角三角形能容纳的正方形边长最大是6017(步).
