2021年全国著名重点中学领航高考冲刺试卷(Word含解析)
文档属性
| 名称 | 2021年全国著名重点中学领航高考冲刺试卷(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览




文档简介
2021年全国著名重点中学领航高考冲刺试卷
数学(第八模拟)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M={x|-4<x≤2},,则M∩N=
A.{2}
B.{x|-4<x≤-2}
C.{x|-4<x≤2}
D.{x|-2≤x≤2}
2.若复数z满足,则复数z的虚部为
A.
B.
C.
D.
3.高三毕业时,甲、乙、丙、丁、戊五名同学站成一排合影留念,其中戊站在正中间,则甲不与戊相邻,乙与戊相邻的站法种数为
A.4
B.8
C.16
D.24
4.函数的大致图象是
A.
B.
C.
D.
5.0.618被公认为是最具有审美意义的比例数字,是最能引起美感的比例,因此被称为黄金分割.被誉为“中国现代数学之父”的著名数学家华罗庚先生倡导的“0.618优选法”在生产和科研实践中得到了非常广泛的应用.他认为底与腰之比为黄金分割比
的黄金三角形是“最美三角形”,即顶角为36°的等腰三角形,例如,中国国旗上的五角星就是由五个“最美三角形”与一个正五边形组成的,如图,在其中一个黄金△ABC中,黄金分割比为.根据以上信息,计算sin
1674°=
A.
B.
C.
D.
6.已知O为△ABC的外接圆圆心,且,则的值为
A.
B.
C.
D.2
7.《九章算术》与《几何原本》并称现代数学的两大源泉.在《九章算术》卷五商功篇中介绍了羡除(此处是指三面为等腰梯形,其他两侧面为直角三角形的五面体)体积的求法.在如图所示的羡除中,平面ABDA′是铅垂面,下宽AA′=3
m,上宽BD=4
m,深3
m,平面BCED是水平面,末端宽CE=5
m,无深,长6
m(直线CE到BD的距离),则该羡除的体积为
A.24
m3
B.30
m3
C.36
m3
D.42
m3
8.已知函数f(x)=ln
x-1,若方程在区间[1,e]内有且仅有一个根,则实数m的取值范围是
A.[1-e,e]
B.[e,1+e]
C.(-∞,1-e]
D.(-∞,e)
二、选择题:在每小题给出的选项中,有多项符合题目要求.
9.已知递减的等差数列{an}的前n项和为Sn,S5=S7,则
A.a6>0
B.S6最大
C.S13>0
D.S11>0
10.已知a,b为正实数,则下列结论正确的是
A.若a>b,则
B.若a<b,m为正实数,则
C.若a≠b,则a3+b3>a2b+ab2
D.若a+b=1,则
11.函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法正确的是
A.
B.函数f(x)图象的对称轴为直线
C.将函数f(x)的图象向左平移个单位长度,得到函数的图象
D.若f(x)在区间上的值域为,则实数a的取值范围为
12.已知点M(2,-2)在抛物线x2=2py(p>0)的准线上,F是抛物线的焦点.过点M的两条直线分别与抛物线相切于点A,B,直线MF交直线AB于点E,则下列结论正确的是
A.抛物线方程为x2=4y
B.直线AB的方程为x-2y+4=0
C.
D.|ME|2=|AE|·|BE|
三、填空题
13.已知函数则_______.
14.甲、乙两名运动员进行羽毛球比赛,比赛采取3局2胜制,已知每局比赛甲胜的概率为,乙胜的概率为,且各局比赛结果互不影响.若第一局甲胜,则本次比赛甲胜的概率是_______.
15.已知F是双曲线C:的左焦点,点Q在直线l1:上,点P在直线l2:上,O为坐标原点,,,△FOP的面积为,则双曲线C的标准方程为___________.
16.在三棱锥D-ABC中,AD⊥平面ABC,AC=3,,,若三棱锥D-ABC的体积为,则此三棱锥的外接球的表面积为_______.
四、解答题:解答应写出文字说明、证明过程或演算步骤.
17.在①,②,③sin
B(sin
B-sin
C)=(sin
A+sin
C)(sin
A-sin
C)这三个条件中任选一个,补充在下面问题中,并作答.
问题:已知△ABC的内角A,B,C的对边分别为a,b,c,且a=2,________,求△ABC面积的最大值.
注:如果选择多个条件分别解答,按第一个解答计分.
18.已知{an}是等差数列,其前n项和为Sn.若a1-1,a2-2,a3-2成等比数列,S5=3(a1+a4).
(1)求{an}的通项公式;
(2)设,数列{bn}的前n项和为Tn,求Tn.
19.如图,在四棱锥S-ABCD中,底面ABCD为矩形,△SAD为等腰直角三角形,
,AB=2,F是BC的中点,二面角S-AD-B的大小等于120°.
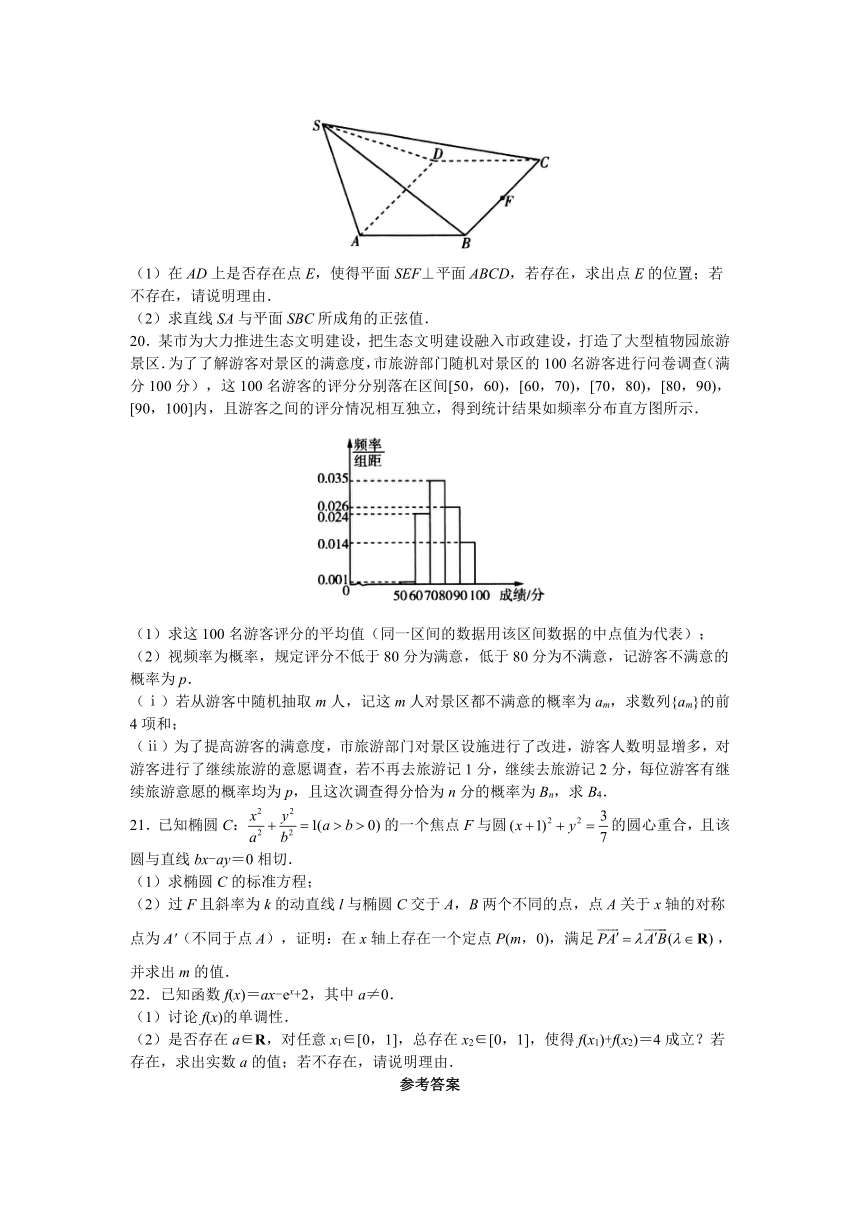
(1)在AD上是否存在点E,使得平面SEF⊥平面ABCD,若存在,求出点E的位置;若不存在,请说明理由.
(2)求直线SA与平面SBC所成角的正弦值.
20.某市为大力推进生态文明建设,把生态文明建设融入市政建设,打造了大型植物园旅游景区.为了了解游客对景区的满意度,市旅游部门随机对景区的100名游客进行问卷调查(满分100分),这100名游客的评分分别落在区间[50,60),[60,70),[70,80),[80,90),[90,100]内,且游客之间的评分情况相互独立,得到统计结果如频率分布直方图所示.
(1)求这100名游客评分的平均值(同一区间的数据用该区间数据的中点值为代表);
(2)视频率为概率,规定评分不低于80分为满意,低于80分为不满意,记游客不满意的概率为p.
(ⅰ)若从游客中随机抽取m人,记这m人对景区都不满意的概率为am,求数列{am}的前4项和;
(ⅱ)为了提高游客的满意度,市旅游部门对景区设施进行了改进,游客人数明显增多,对游客进行了继续旅游的意愿调查,若不再去旅游记1分,继续去旅游记2分,每位游客有继续旅游意愿的概率均为p,且这次调查得分恰为n分的概率为Bn,求B4.
21.已知椭圆C:的一个焦点F与圆的圆心重合,且该圆与直线bx-ay=0相切.
(1)求椭圆C的标准方程;
(2)过F且斜率为k的动直线l与椭圆C交于A,B两个不同的点,点A关于x轴的对称点为A′(不同于点A),证明:在x轴上存在一个定点P(m,0),满足,并求出m的值.
22.已知函数f(x)=ax-ex+2,其中a≠0.
(1)讨论f(x)的单调性.
(2)是否存在a∈R,对任意x1∈[0,1],总存在x2∈[0,1],使得f(x1)+f(x2)=4成立?若存在,求出实数a的值;若不存在,请说明理由.
参考答案
详解详析
一、选择题
1.B
【关键能力】
本题考查运算求解能力.
【解析】
解法一
因为M={x|-4<x≤2},
,所以M∩N={x|-4<x≤-2},故选B.
解法二
易得2?N,所以2?M∩N,故排除A,C,D,故选B.
2.A
【关键能力】
本题考查运算求解能力.
【解析】
由题意,得,其虚部为,故选A.
3.B
【试题情境】
本题是应用性、创新性题目,属于生活实践情境.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【解析】
由题可知,戊站在正中间,位置确定,则只需排其余四人即可,则甲不与戊相邻,乙与戊相邻的站法有(种),故选B.
4.C
【试题情境】
本题是基础性题目,属于课程学习情境,具体是数学运算学习情境.
【必备知识】
本题考查的知识是会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.
【关键能力】
本题考查运算求解能力.
【解题思路】
结合选项中函数图象的特征,利用函数的性质,采用排除法求解即可.
【解析】
由题可知,函数f(x)的定义域为(-∞,0)∪(0,+∞),
,所以函数f(x)为奇函数,所以排除选项BD;又f(1)=0,所以排除选项A.故选C.
5.B
【试题情境】
本题是应用性、创新性题目,属于生活实践情境,以黄金三角形为载体考查三角知识.
【关键能力】
本题考查运算求解能力、创新能力.
【解析】
在△ABC中,由正弦定理可得
,∴,∴
.故选B.
6.C
【关键能力】
本题考查逻辑思维能力和运算求解能力.
【解题思路】
利用向量数量积的定义求出已知等式两端的数量积,又点O为△ABC的外心,由向量投影的概念表示出向量在向量方向上的投影与向量在向量方向上的投影,进而求得结果.
【解析】
如图,,,由O为△ABC的外心,得向量在向量方向上的投影为,向量在向量方向上的投影为,即,,,从而
,即,因而,故选C.
解题关键
求解本题的关键是利用向量投影的概念进行运算,同时得到关系式
后,不要轻易约分,而是利用外心的定义转化为来求解.
7.C
【试题情境】
本题是应用性、创新性题目,属于生活实践情境,以《九章算术》中的羡除为载体考查多面体体积的求解.
【关键能力】
本题考查空间想象能力、逻辑思维能力、运算求解能力.
【学科素养】
本题以中国古代数学文化中的羡除为背景设题,通过对几何体的分割计算其体积,考查数学探索、数学应用学科素养.
【解题思路】
观察几何体的结构特征,合理分割,将不规则几何体体积的计算转化为锥体、柱体体积的计算.
【解析】
如图,在BD,CE上分别取点B′,C′,使得BB′=CC′=3
m,连接A′B′,A′C′,B′C′,则三棱柱ABC-A′B′C′是斜三棱柱,该羡除的体积
.
8.A
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【学科素养】
试题以函数与导数的知识为依托,很好地考查了考生对函数与方程间的关系的理解与应用,对思维的深度、解题的灵活性均有较高要求,考查的学科素养是理性思维、数学探索.
【解题思路】
方程
【解析】
方程等价于,等价于(ln
x-1)ex+x-m=0.令g(x)=(ln
x-1)ex+x-m(x∈[1,e]),由题意知函数g(x)有且仅有一个零点,则,令,则,所以函数h(x)在[1,e]上单调递增,所以当x∈[1,e]时,h(x)≥h(1)=0,所以g′(x)>0,所以g(x)在[1,e]上单调递增,所以g(x)min=g(1)=1-e-m,g(x)max=g(e)=e-m,所以要使函数g(x)在区间[1,e]内有且仅有一个零点,需解得1-e≤m≤e,即实数m的取值范围是[1-e,e].
方法技巧
已知函数零点(方程根)的个数,求参数的取值范围问题的三种常用方法:(1)直接法,直接根据题设条件构建关于参数的不等式(组),再通过解不等式(组)确定参数的范围;(2)分离参数法,先分离参数,将问题转化成求函数值域问题加以解决;(3)数形结合法,先对解析式变形,在同一平面直角坐标系中作出函数图象,然后数形结合求解.
二、选择题
9.ABD
【试题情境】
本题是基础性题目,属于课程学习情境,具体是数学运算学习情境.
【关键能力】
本题考查运算求解能力.
【解题思路】
由S5=S7可得a6+a7=0,结合数列{an}递减可得a6>0,a7<0,从而可得S6最大,最后利用等差数列的前n项和公式以及等差数列的性质判断C,D选项即可.
【解析】
因为S5=S7,所以S7-S5=0,即a6+a7=0,因为数列{an}递减,所以a6>a7,则a6>0,a7<0,所以S6最大;因为Sn为等差数列{an}的前n项和,所以
,.故选ABD.
10.ACD
【试题情境】
本题是基础性题目,属于课程学习情境,具体是数学运算学习情境,综合考查作差法及基本不等式的应用.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【解题思路】
利用作差法及基本不等式逐一判断即可.
【解析】
对于A,因为a,b为正实数,且a>b,所以,所以,故A正确;对于B,因为a,b,m均为正实数,且a<b,所以,所以,故B错误;
对于C,因为a,b为正实数,a≠b,所以a3+b3-(a2b+ab2)=(a-b)2(a+b)>0,所以a3+b3>a2b+ab2,C正确;
对于D,
,当且仅当a=b时等号成立,故D正确.故选ACD.
11.ABD
【试题情境】
本题是综合性题目,属于探索创新情境,具体是数学探究情境.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【学科素养】
试题以考查三角函数的图象与性质为目标,选取正弦型函数为材料,通过分析函数图象的特征,考查理性思维、数学应用、数学探索学科素养.
【解析】
由图可知A=2,设函数f(x)的最小正周期为T,则,∴T=π,∴ω=2,则f(x)=2sin(2x+φ).由得,又|φ|<π,∴,∴,A正确;
由,得
,故B正确;
将函数f(x)的图象向左平移个单位长度,得
的图象,故C错误;
由,得,由y=2sin
t的图象可知,要使函数f(x)在区间上的值域为,则
,解得,故D正确.故选ABD.
12.BCD
【试题情境】
本题是综合性题目,属于探索创新情境,具体是数学探究情境.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【学科素养】
本题以直线与抛物线相切为载体考查抛物线的几何性质及直线与抛物线的位置关系,考查考生运用所学知识分析问题与解决问题的能力,充分体现了理性思维、数学应用、数学探索学科素养.
【解析】
因为点M(2,-2)在抛物线x2=2py(p>0)的准线上,所以,p=4,抛物线的方程为x2=8y,故A错误.
设A(x1,y1),B(x2,y2),则抛物线在A,B两点处的切线方程分别为x1x=4(y1+y)和x2x=4(y2+y),因为两直线均过点M(2,-2),所以x1=2(y1-2),x2=2(y2-2),则点A(x1,y1),B(x2,y2)均在直线x=2(y-2)上,所以直线AB的方程为x=2(y-2),即x-2y+4=0,故B正确.
联立直线AB与抛物线的方程得得x2-4x-16=0,所以x1x2=-16,所以,所以AM⊥BM,,故C正确.
又,,所以,所以ME⊥AB,所以|ME|2=|AE|·|BE|.故选BCD.
三、填空题
13.
【关键能力】
本题考查运算求解能力.
【解析】
由题意得.
14.
【试题情境】
本题是应用性题目,属于生活实践情境,以羽毛球比赛为背景考查相互独立事件概率的求解.
【关键能力】
本题考查数学建模能力、运算求解能力.
【解题思路】
先分析出甲最终获胜有2种情况,再分别求出每种情况下甲胜的概率,相加即可得本次比赛甲胜的概率.
【解析】
已知第一局甲胜,则甲最终获胜有2种情况:甲第二局胜,比赛2局;甲第二局输、第三局胜,比赛3局.记甲第二局胜为事件A,则,记甲第二局输、第三局胜为事件B,则,所以甲胜的概率.
15.
【试题情境】
本题是综合性题目,属于探索创新情境,具体是数学探究情境,以双曲线为载体考查直线、双曲线和平面向量的相关知识.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【解题思路】
,
【解析】
由,,得OQ是线段FP的垂直平分线,所以∠FOQ=∠POQ=∠POx=60°,所以,,,所以△FOP的面积为,解得c=2.又a2+b2=c2,,所以a=1,,所以双曲线C的标准方程为.
16.20π
【必备知识】
本题考查的知识是点、直线、平面之间的位置关系,了解球、棱柱、棱锥、台的表面积和体积的计算公式.
【关键能力】
本题考查空间想象能力、逻辑思维能力、运算求解能力.
【解题思路】
设出外接球的半径R、球心O,△ABC的外心O1、半径r
【解析】
设三棱锥外接球的半径为R、球心为O,△ABC的外心为O1、外接圆的半径为r,连接AO1,过O作AO1的平行线OE交AD于E,连接OA,OD,如图所示,则OA=OD=R,O1A=r,OE⊥AD,所以E为AD的中点.在△ABC中,由正弦定理得,解得.在△ABC中,由余弦定理BC2=AB2+AC2-2AB·AC·cos∠BAC,
可得,得AB=4.
所以
.
因为,所以.连接OO1,易知OO1∥AD,所以四边形EAO1O为平行四边形,,所以
.所以该三棱锥的外接球的表面积
.
四、解答题
17.【必备知识】
本题考查的知识是掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题及能进行简单的恒等变换.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
解:方案一:选条件①.
因为,
所以
,
所以,又0<A<π,所以.
由余弦定理得b2+c2-a2=2bccos
A,
所以b2+c2-bc=4≥bc,
所以bc≤4,当且仅当b=c时取等号.
所以,
所以△ABC面积的最大值为.
方案二:选条件②.
因为,
所以
,
因为0<A<π,所以tan
B≠0,tan
C≠0,所以,所以.
由余弦定理得b2+c2-a2=2bccos
A,
所以b2+c2-bc=4≥bc,
所以bc≤4,当且仅当b=c时取等号.
所以
,
所以△ABC面积的最大值为.
方案三:选条件③.
因为sin
B(sin
B-sin
C)=(sin
A+sin
C)(sin
A-sin
C),
所以由正弦定理得b2+c2-a2=bc,
由余弦定理得,
又0<A<π,所以.
由余弦定理得b2+c2-a2=2bccos
A,
所以b2+c2-bc=4≥bc,
所以bc≤4,当且仅当b=c时取等号.
所以,
所以△ABC面积的最大值为.
18.【必备知识】
本题考查的知识是掌握等差数列、等比数列的通项公式与前n项和公式.
【关键能力】
本题考查运算求解能力.
【解题思路】
(1)先利用等差数列的通项公式及前n项和公式、等比数列的性质求出首项和公差,即可得解;(2)先求数列{bn}的通项,再利用分组求和法求解.
解:(1)设等差数列{an}的公差为d.因为a1-1,a2-2,a3-2成等比数列,
所以(a1+d-2)2=(a1-1)(a1+2d-2),即d2-2d=a1-2,①
因为S5=3(a1+a4),所以,即a1=d,②
由①②得a1=1,d=1或a1=2,d=2.
当a1=1,d=1时,a1-1=0,与a1-1,a2-2,a3-2成等比数列矛盾,
所以a1=2,d=2,所以an=2+(n-1)×2=2n.
(2)由(1)得,
所以Tn=(2+4+6+…+2n)+(41+42+…+4n)
.
方法技巧
数列求和的常用方法
(1)公式法:即直接用等差、等比数列的求和公式求和.
(2)错位相减法:若{an}是等差数列,{bn}是等比数列,求a1b1+a2b2+…+anbn.
(3)裂项相消法:把数列的通项拆成两项之差,相消剩下首尾的若干项.常见的裂顶有,,等.
(4)分组求和法:把数列的每一项分成若干项,使其转化为等差或等比数列,再求和.
(5)倒序相加法.
19.【必备知识】
本题考查的知识是点、直线、平面之间的位置关系,能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用.
【关键能力】
本题考查逻辑思维能力、空间想象能力与运算求解能力.
【解题思路】
(1)取AD的中点E,连接EF,SE,SF
(2)由(1)知∠SEF就是二面角S-AD-B的平面角∠SEF=120°建立空间直角坐标系E-xyz相关点及向量的坐标平面SBC的一个法向量直线SA与平面SBC所成角的正弦值
解:(1)在线段AD上存在点E满足题意,且E为AD的中点.
如图,连接EF,SE,SF,
∵四边形ABCD是矩形,∴AB⊥AD.
又E,F分别是AD,BC的中点,∴EF∥AB,AD⊥EF.∵△SAD为等腰直角三角形,SA=SD,E为AD的中点,∴SE⊥AD.∵SE∩EF=E,SE?平面SEF,EF?平面SEF,∴AD⊥平面SEF.
又AD?平面ABCD,∴平面SEF⊥平面ABCD.
故AD上存在中点E,使得平面SEF⊥平面ABCD.
(2)解法一
由(1)可知∠SEF就是二面角S-AD-B的平面角,∴∠SEF=120°.
以E为坐标原点,,的方向分别为x,y轴正方向,建立如图所示的空间直角坐标系E-xyz,
由△SAD为等腰直角三角形,,得,
.
可得,A(2,0,0),B(2,2,0),C(-2,2,0),∴,,,
设是平面SBC的法向量,
则即
可取.
设直线SA与平面SBC所成的角为θ,
则,∴直线SA与平面SBC所成角的正弦值为.
解法二
过点E作EG⊥SF于点G,由(1)知,AD⊥平面SEF,则BC⊥平面SEF,BC⊥EG,又SF∩BC=F,∴EG⊥平面SBC,易知AE∥平面SBC,则点A到平面SBC的距离等于EG.
由(1)可知∠SEF就是二面角S-AD-B的平面角,∴∠SEF=120°.
由△SAD为等腰直角三角形,,得,
.
又EF=AB=2,∴EG=1.
设直线SA与平面SBC所成的角为θ,
则
,
即直线SA与平面SBC所成角的正弦值为.
方法技巧
求解线段上点的位置的探索性问题,一般是先根据条件猜测点的位置,再给出证明,所求点多为中点或三等分点中某一个,也可以根据相似知识找点,求解时注意中位线的性质及三点共线条件的应用.
20.【试题情境】
本题是综合性、应用性、创新性题目,属于生活实践情境.
【关键能力】
本题考查数学建模能力、逻辑思维能力和创新能力.
【解题思路】
(1)由频率分布直方图与平均数计算公式求解即可.(2)(ⅰ)先利用频率分布直方图,求出随机抽取一名游客,该游客对景区不满意的概率,再利用相互独立事件的概率求解{am}的通项公式,最后利用等比数列的前n项和公式求解;(ⅱ)根据题意求出B1,B2及Bn与Bn-1,Bn-2(n≥3,n∈N
)的关系式,代入计算即可.
解:(1)这100名游客评分的平均值为
55×0.01+65×0.24+75×0.35+85×0.26+95×0.14=77.8(分).
(2)(ⅰ)由题得,
所以,
所以数列{am}的前4项和为.
(ⅱ)由题意得,,
则,则
.所以.
21.【关键能力】
本题考查逻辑思维能力、运算求解能力.
【学科素养】
试题以椭圆与圆为背景,很好地考查了考生对直线与圆相切的理解与应用,对三点共线的理解与应用,对方程思想与设而不求思想的应用,体现了理性思维、数学应用、数学探索学科素养.
【解题思路】(1)
(2)设直线l:y=k(x+1)关于x的一元二次方程
解:(1)因为圆的圆心为(-1,0),半径为,
所以椭圆C的左焦点F(-1,0),则c=1,a2-b2=1
①.
由圆与直线bx-ay=0相切,得
②,
由①②解得a=2,,
故椭圆C的标准方程为.
(2)由题意设直线l的方程为y=k(x+1).
由得(4k2+3)x2+8k2x+4k2-12=0.
设A(x1,y1),B(x2,y2),则,.
由得P,A′,B三点共线,所以直线PA,PB的斜率互为相反数.
又直线PA,PB的斜率分别为,,
所以,
所以x2y1+x1y2-m(y1+y2)=0,
所以x2k(x1+1)+x1k(x2+1)-m[k(x1+1)+k(x2+1)]=0,
所以2kx1x2+
k(x1+x2)-m[k(x1+x2)+2k]=0,
所以,
所以k(m+4)=0,
若k(m+4)=0对任意k∈R恒成立,则m=-4.
故在x轴上存在一个定点P(m,0),满足,且m的值为-4.
22.【必备知识】
本题考查的知识是能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,了解函数的单调性与导数的关系;能利用导数研究函数的单调性,会求函数的单调区间,会求闭区间上函数的最大值、最小值.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【解题思路】
(1)
(2)当a≤1,且a≠0时f(x)在[0,1]上单调递减x∈[0,1]时,
解:(1)由f(x)=ax-ex+2,得f′(x)=a-ex.
当a<0时,对任意x∈(-∞,+∞),f′(x)<0,所以f(x)单调递减.
当a>0时,令f′(x)=0,得x=ln
a,
当x∈(-∞,ln
a)时,f′(x)>0,当x∈(ln
a,+∞)时,f′(x)<0,
所以f(x)在(-∞,ln
a)上单调递增,在(ln
a,+∞)上单调递减.
综上所述,当a<0时,f(x)在(-∞,+∞)上单调递减;当a>0时,f(x)在(-∞,ln
a)上单调递增,在(ln
a,+∞)上单调递减.
(2)存在满足条件的实数a,且实数a的值为e+1.
理由如下:
①当a≤1,且a≠0时,由(1)知,f(x)在[0,1]上单调递减,
则x∈[0,1]时,f(x)max=f(0)=1,
则f(x1)+f(x2)≤2f(0)=2<4.
所以此时不满足题意.
②当1<a<e时,由(1)知,在[0,ln
a]上,f(x)单调递增,在(ln
a,1]上,f(x)单调递减,
则当x∈[0,1]时,f(x)max=f(ln
a)=aln
a-a+2.
当x1=0时,对任意x2∈[0,1],
f(x1)+f(x2)≤f(0)+f(ln
a)=1+aln
a-a+2=a(ln
a-1)+3<3.
所以此时不满足题意.
③当a≥e时,令g(x)=4-f(x)(x∈[0,1]),
由(1)知,f(x)在[0,1]上单调递增,进而知g(x)在[0,1]上单调递减,
所以g(x)max=g(0)=4-f(0),g(x)min=g(1)=4-f(1).
若对任意的x1∈[0,1],总存在x2∈[0,1],使得f(x1)+f(x2)=4,
则f(x1)=g(x2),即
所以f(0)+f(1)=a-e+3=4,解得a=e+1.
综上,存在满足题意的实数a,且实数a的值为e+1.
方法技巧
利用导数研究函数的单调性的一般步骤:①确定函数的定义域;②求导函数;③若求单调区间(或证明单调性),只需在函数的定义域内解(或证明)不等式f′(x)≥0或f′(x)≤0(不恒等于0)即可.
数学(第八模拟)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M={x|-4<x≤2},,则M∩N=
A.{2}
B.{x|-4<x≤-2}
C.{x|-4<x≤2}
D.{x|-2≤x≤2}
2.若复数z满足,则复数z的虚部为
A.
B.
C.
D.
3.高三毕业时,甲、乙、丙、丁、戊五名同学站成一排合影留念,其中戊站在正中间,则甲不与戊相邻,乙与戊相邻的站法种数为
A.4
B.8
C.16
D.24
4.函数的大致图象是
A.
B.
C.
D.
5.0.618被公认为是最具有审美意义的比例数字,是最能引起美感的比例,因此被称为黄金分割.被誉为“中国现代数学之父”的著名数学家华罗庚先生倡导的“0.618优选法”在生产和科研实践中得到了非常广泛的应用.他认为底与腰之比为黄金分割比
的黄金三角形是“最美三角形”,即顶角为36°的等腰三角形,例如,中国国旗上的五角星就是由五个“最美三角形”与一个正五边形组成的,如图,在其中一个黄金△ABC中,黄金分割比为.根据以上信息,计算sin
1674°=
A.
B.
C.
D.
6.已知O为△ABC的外接圆圆心,且,则的值为
A.
B.
C.
D.2
7.《九章算术》与《几何原本》并称现代数学的两大源泉.在《九章算术》卷五商功篇中介绍了羡除(此处是指三面为等腰梯形,其他两侧面为直角三角形的五面体)体积的求法.在如图所示的羡除中,平面ABDA′是铅垂面,下宽AA′=3
m,上宽BD=4
m,深3
m,平面BCED是水平面,末端宽CE=5
m,无深,长6
m(直线CE到BD的距离),则该羡除的体积为
A.24
m3
B.30
m3
C.36
m3
D.42
m3
8.已知函数f(x)=ln
x-1,若方程在区间[1,e]内有且仅有一个根,则实数m的取值范围是
A.[1-e,e]
B.[e,1+e]
C.(-∞,1-e]
D.(-∞,e)
二、选择题:在每小题给出的选项中,有多项符合题目要求.
9.已知递减的等差数列{an}的前n项和为Sn,S5=S7,则
A.a6>0
B.S6最大
C.S13>0
D.S11>0
10.已知a,b为正实数,则下列结论正确的是
A.若a>b,则
B.若a<b,m为正实数,则
C.若a≠b,则a3+b3>a2b+ab2
D.若a+b=1,则
11.函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法正确的是
A.
B.函数f(x)图象的对称轴为直线
C.将函数f(x)的图象向左平移个单位长度,得到函数的图象
D.若f(x)在区间上的值域为,则实数a的取值范围为
12.已知点M(2,-2)在抛物线x2=2py(p>0)的准线上,F是抛物线的焦点.过点M的两条直线分别与抛物线相切于点A,B,直线MF交直线AB于点E,则下列结论正确的是
A.抛物线方程为x2=4y
B.直线AB的方程为x-2y+4=0
C.
D.|ME|2=|AE|·|BE|
三、填空题
13.已知函数则_______.
14.甲、乙两名运动员进行羽毛球比赛,比赛采取3局2胜制,已知每局比赛甲胜的概率为,乙胜的概率为,且各局比赛结果互不影响.若第一局甲胜,则本次比赛甲胜的概率是_______.
15.已知F是双曲线C:的左焦点,点Q在直线l1:上,点P在直线l2:上,O为坐标原点,,,△FOP的面积为,则双曲线C的标准方程为___________.
16.在三棱锥D-ABC中,AD⊥平面ABC,AC=3,,,若三棱锥D-ABC的体积为,则此三棱锥的外接球的表面积为_______.
四、解答题:解答应写出文字说明、证明过程或演算步骤.
17.在①,②,③sin
B(sin
B-sin
C)=(sin
A+sin
C)(sin
A-sin
C)这三个条件中任选一个,补充在下面问题中,并作答.
问题:已知△ABC的内角A,B,C的对边分别为a,b,c,且a=2,________,求△ABC面积的最大值.
注:如果选择多个条件分别解答,按第一个解答计分.
18.已知{an}是等差数列,其前n项和为Sn.若a1-1,a2-2,a3-2成等比数列,S5=3(a1+a4).
(1)求{an}的通项公式;
(2)设,数列{bn}的前n项和为Tn,求Tn.
19.如图,在四棱锥S-ABCD中,底面ABCD为矩形,△SAD为等腰直角三角形,
,AB=2,F是BC的中点,二面角S-AD-B的大小等于120°.
(1)在AD上是否存在点E,使得平面SEF⊥平面ABCD,若存在,求出点E的位置;若不存在,请说明理由.
(2)求直线SA与平面SBC所成角的正弦值.
20.某市为大力推进生态文明建设,把生态文明建设融入市政建设,打造了大型植物园旅游景区.为了了解游客对景区的满意度,市旅游部门随机对景区的100名游客进行问卷调查(满分100分),这100名游客的评分分别落在区间[50,60),[60,70),[70,80),[80,90),[90,100]内,且游客之间的评分情况相互独立,得到统计结果如频率分布直方图所示.
(1)求这100名游客评分的平均值(同一区间的数据用该区间数据的中点值为代表);
(2)视频率为概率,规定评分不低于80分为满意,低于80分为不满意,记游客不满意的概率为p.
(ⅰ)若从游客中随机抽取m人,记这m人对景区都不满意的概率为am,求数列{am}的前4项和;
(ⅱ)为了提高游客的满意度,市旅游部门对景区设施进行了改进,游客人数明显增多,对游客进行了继续旅游的意愿调查,若不再去旅游记1分,继续去旅游记2分,每位游客有继续旅游意愿的概率均为p,且这次调查得分恰为n分的概率为Bn,求B4.
21.已知椭圆C:的一个焦点F与圆的圆心重合,且该圆与直线bx-ay=0相切.
(1)求椭圆C的标准方程;
(2)过F且斜率为k的动直线l与椭圆C交于A,B两个不同的点,点A关于x轴的对称点为A′(不同于点A),证明:在x轴上存在一个定点P(m,0),满足,并求出m的值.
22.已知函数f(x)=ax-ex+2,其中a≠0.
(1)讨论f(x)的单调性.
(2)是否存在a∈R,对任意x1∈[0,1],总存在x2∈[0,1],使得f(x1)+f(x2)=4成立?若存在,求出实数a的值;若不存在,请说明理由.
参考答案
详解详析
一、选择题
1.B
【关键能力】
本题考查运算求解能力.
【解析】
解法一
因为M={x|-4<x≤2},
,所以M∩N={x|-4<x≤-2},故选B.
解法二
易得2?N,所以2?M∩N,故排除A,C,D,故选B.
2.A
【关键能力】
本题考查运算求解能力.
【解析】
由题意,得,其虚部为,故选A.
3.B
【试题情境】
本题是应用性、创新性题目,属于生活实践情境.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【解析】
由题可知,戊站在正中间,位置确定,则只需排其余四人即可,则甲不与戊相邻,乙与戊相邻的站法有(种),故选B.
4.C
【试题情境】
本题是基础性题目,属于课程学习情境,具体是数学运算学习情境.
【必备知识】
本题考查的知识是会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.
【关键能力】
本题考查运算求解能力.
【解题思路】
结合选项中函数图象的特征,利用函数的性质,采用排除法求解即可.
【解析】
由题可知,函数f(x)的定义域为(-∞,0)∪(0,+∞),
,所以函数f(x)为奇函数,所以排除选项BD;又f(1)=0,所以排除选项A.故选C.
5.B
【试题情境】
本题是应用性、创新性题目,属于生活实践情境,以黄金三角形为载体考查三角知识.
【关键能力】
本题考查运算求解能力、创新能力.
【解析】
在△ABC中,由正弦定理可得
,∴,∴
.故选B.
6.C
【关键能力】
本题考查逻辑思维能力和运算求解能力.
【解题思路】
利用向量数量积的定义求出已知等式两端的数量积,又点O为△ABC的外心,由向量投影的概念表示出向量在向量方向上的投影与向量在向量方向上的投影,进而求得结果.
【解析】
如图,,,由O为△ABC的外心,得向量在向量方向上的投影为,向量在向量方向上的投影为,即,,,从而
,即,因而,故选C.
解题关键
求解本题的关键是利用向量投影的概念进行运算,同时得到关系式
后,不要轻易约分,而是利用外心的定义转化为来求解.
7.C
【试题情境】
本题是应用性、创新性题目,属于生活实践情境,以《九章算术》中的羡除为载体考查多面体体积的求解.
【关键能力】
本题考查空间想象能力、逻辑思维能力、运算求解能力.
【学科素养】
本题以中国古代数学文化中的羡除为背景设题,通过对几何体的分割计算其体积,考查数学探索、数学应用学科素养.
【解题思路】
观察几何体的结构特征,合理分割,将不规则几何体体积的计算转化为锥体、柱体体积的计算.
【解析】
如图,在BD,CE上分别取点B′,C′,使得BB′=CC′=3
m,连接A′B′,A′C′,B′C′,则三棱柱ABC-A′B′C′是斜三棱柱,该羡除的体积
.
8.A
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【学科素养】
试题以函数与导数的知识为依托,很好地考查了考生对函数与方程间的关系的理解与应用,对思维的深度、解题的灵活性均有较高要求,考查的学科素养是理性思维、数学探索.
【解题思路】
方程
【解析】
方程等价于,等价于(ln
x-1)ex+x-m=0.令g(x)=(ln
x-1)ex+x-m(x∈[1,e]),由题意知函数g(x)有且仅有一个零点,则,令,则,所以函数h(x)在[1,e]上单调递增,所以当x∈[1,e]时,h(x)≥h(1)=0,所以g′(x)>0,所以g(x)在[1,e]上单调递增,所以g(x)min=g(1)=1-e-m,g(x)max=g(e)=e-m,所以要使函数g(x)在区间[1,e]内有且仅有一个零点,需解得1-e≤m≤e,即实数m的取值范围是[1-e,e].
方法技巧
已知函数零点(方程根)的个数,求参数的取值范围问题的三种常用方法:(1)直接法,直接根据题设条件构建关于参数的不等式(组),再通过解不等式(组)确定参数的范围;(2)分离参数法,先分离参数,将问题转化成求函数值域问题加以解决;(3)数形结合法,先对解析式变形,在同一平面直角坐标系中作出函数图象,然后数形结合求解.
二、选择题
9.ABD
【试题情境】
本题是基础性题目,属于课程学习情境,具体是数学运算学习情境.
【关键能力】
本题考查运算求解能力.
【解题思路】
由S5=S7可得a6+a7=0,结合数列{an}递减可得a6>0,a7<0,从而可得S6最大,最后利用等差数列的前n项和公式以及等差数列的性质判断C,D选项即可.
【解析】
因为S5=S7,所以S7-S5=0,即a6+a7=0,因为数列{an}递减,所以a6>a7,则a6>0,a7<0,所以S6最大;因为Sn为等差数列{an}的前n项和,所以
,.故选ABD.
10.ACD
【试题情境】
本题是基础性题目,属于课程学习情境,具体是数学运算学习情境,综合考查作差法及基本不等式的应用.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【解题思路】
利用作差法及基本不等式逐一判断即可.
【解析】
对于A,因为a,b为正实数,且a>b,所以,所以,故A正确;对于B,因为a,b,m均为正实数,且a<b,所以,所以,故B错误;
对于C,因为a,b为正实数,a≠b,所以a3+b3-(a2b+ab2)=(a-b)2(a+b)>0,所以a3+b3>a2b+ab2,C正确;
对于D,
,当且仅当a=b时等号成立,故D正确.故选ACD.
11.ABD
【试题情境】
本题是综合性题目,属于探索创新情境,具体是数学探究情境.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【学科素养】
试题以考查三角函数的图象与性质为目标,选取正弦型函数为材料,通过分析函数图象的特征,考查理性思维、数学应用、数学探索学科素养.
【解析】
由图可知A=2,设函数f(x)的最小正周期为T,则,∴T=π,∴ω=2,则f(x)=2sin(2x+φ).由得,又|φ|<π,∴,∴,A正确;
由,得
,故B正确;
将函数f(x)的图象向左平移个单位长度,得
的图象,故C错误;
由,得,由y=2sin
t的图象可知,要使函数f(x)在区间上的值域为,则
,解得,故D正确.故选ABD.
12.BCD
【试题情境】
本题是综合性题目,属于探索创新情境,具体是数学探究情境.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【学科素养】
本题以直线与抛物线相切为载体考查抛物线的几何性质及直线与抛物线的位置关系,考查考生运用所学知识分析问题与解决问题的能力,充分体现了理性思维、数学应用、数学探索学科素养.
【解析】
因为点M(2,-2)在抛物线x2=2py(p>0)的准线上,所以,p=4,抛物线的方程为x2=8y,故A错误.
设A(x1,y1),B(x2,y2),则抛物线在A,B两点处的切线方程分别为x1x=4(y1+y)和x2x=4(y2+y),因为两直线均过点M(2,-2),所以x1=2(y1-2),x2=2(y2-2),则点A(x1,y1),B(x2,y2)均在直线x=2(y-2)上,所以直线AB的方程为x=2(y-2),即x-2y+4=0,故B正确.
联立直线AB与抛物线的方程得得x2-4x-16=0,所以x1x2=-16,所以,所以AM⊥BM,,故C正确.
又,,所以,所以ME⊥AB,所以|ME|2=|AE|·|BE|.故选BCD.
三、填空题
13.
【关键能力】
本题考查运算求解能力.
【解析】
由题意得.
14.
【试题情境】
本题是应用性题目,属于生活实践情境,以羽毛球比赛为背景考查相互独立事件概率的求解.
【关键能力】
本题考查数学建模能力、运算求解能力.
【解题思路】
先分析出甲最终获胜有2种情况,再分别求出每种情况下甲胜的概率,相加即可得本次比赛甲胜的概率.
【解析】
已知第一局甲胜,则甲最终获胜有2种情况:甲第二局胜,比赛2局;甲第二局输、第三局胜,比赛3局.记甲第二局胜为事件A,则,记甲第二局输、第三局胜为事件B,则,所以甲胜的概率.
15.
【试题情境】
本题是综合性题目,属于探索创新情境,具体是数学探究情境,以双曲线为载体考查直线、双曲线和平面向量的相关知识.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【解题思路】
,
【解析】
由,,得OQ是线段FP的垂直平分线,所以∠FOQ=∠POQ=∠POx=60°,所以,,,所以△FOP的面积为,解得c=2.又a2+b2=c2,,所以a=1,,所以双曲线C的标准方程为.
16.20π
【必备知识】
本题考查的知识是点、直线、平面之间的位置关系,了解球、棱柱、棱锥、台的表面积和体积的计算公式.
【关键能力】
本题考查空间想象能力、逻辑思维能力、运算求解能力.
【解题思路】
设出外接球的半径R、球心O,△ABC的外心O1、半径r
【解析】
设三棱锥外接球的半径为R、球心为O,△ABC的外心为O1、外接圆的半径为r,连接AO1,过O作AO1的平行线OE交AD于E,连接OA,OD,如图所示,则OA=OD=R,O1A=r,OE⊥AD,所以E为AD的中点.在△ABC中,由正弦定理得,解得.在△ABC中,由余弦定理BC2=AB2+AC2-2AB·AC·cos∠BAC,
可得,得AB=4.
所以
.
因为,所以.连接OO1,易知OO1∥AD,所以四边形EAO1O为平行四边形,,所以
.所以该三棱锥的外接球的表面积
.
四、解答题
17.【必备知识】
本题考查的知识是掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题及能进行简单的恒等变换.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
解:方案一:选条件①.
因为,
所以
,
所以,又0<A<π,所以.
由余弦定理得b2+c2-a2=2bccos
A,
所以b2+c2-bc=4≥bc,
所以bc≤4,当且仅当b=c时取等号.
所以,
所以△ABC面积的最大值为.
方案二:选条件②.
因为,
所以
,
因为0<A<π,所以tan
B≠0,tan
C≠0,所以,所以.
由余弦定理得b2+c2-a2=2bccos
A,
所以b2+c2-bc=4≥bc,
所以bc≤4,当且仅当b=c时取等号.
所以
,
所以△ABC面积的最大值为.
方案三:选条件③.
因为sin
B(sin
B-sin
C)=(sin
A+sin
C)(sin
A-sin
C),
所以由正弦定理得b2+c2-a2=bc,
由余弦定理得,
又0<A<π,所以.
由余弦定理得b2+c2-a2=2bccos
A,
所以b2+c2-bc=4≥bc,
所以bc≤4,当且仅当b=c时取等号.
所以,
所以△ABC面积的最大值为.
18.【必备知识】
本题考查的知识是掌握等差数列、等比数列的通项公式与前n项和公式.
【关键能力】
本题考查运算求解能力.
【解题思路】
(1)先利用等差数列的通项公式及前n项和公式、等比数列的性质求出首项和公差,即可得解;(2)先求数列{bn}的通项,再利用分组求和法求解.
解:(1)设等差数列{an}的公差为d.因为a1-1,a2-2,a3-2成等比数列,
所以(a1+d-2)2=(a1-1)(a1+2d-2),即d2-2d=a1-2,①
因为S5=3(a1+a4),所以,即a1=d,②
由①②得a1=1,d=1或a1=2,d=2.
当a1=1,d=1时,a1-1=0,与a1-1,a2-2,a3-2成等比数列矛盾,
所以a1=2,d=2,所以an=2+(n-1)×2=2n.
(2)由(1)得,
所以Tn=(2+4+6+…+2n)+(41+42+…+4n)
.
方法技巧
数列求和的常用方法
(1)公式法:即直接用等差、等比数列的求和公式求和.
(2)错位相减法:若{an}是等差数列,{bn}是等比数列,求a1b1+a2b2+…+anbn.
(3)裂项相消法:把数列的通项拆成两项之差,相消剩下首尾的若干项.常见的裂顶有,,等.
(4)分组求和法:把数列的每一项分成若干项,使其转化为等差或等比数列,再求和.
(5)倒序相加法.
19.【必备知识】
本题考查的知识是点、直线、平面之间的位置关系,能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用.
【关键能力】
本题考查逻辑思维能力、空间想象能力与运算求解能力.
【解题思路】
(1)取AD的中点E,连接EF,SE,SF
(2)由(1)知∠SEF就是二面角S-AD-B的平面角∠SEF=120°建立空间直角坐标系E-xyz相关点及向量的坐标平面SBC的一个法向量直线SA与平面SBC所成角的正弦值
解:(1)在线段AD上存在点E满足题意,且E为AD的中点.
如图,连接EF,SE,SF,
∵四边形ABCD是矩形,∴AB⊥AD.
又E,F分别是AD,BC的中点,∴EF∥AB,AD⊥EF.∵△SAD为等腰直角三角形,SA=SD,E为AD的中点,∴SE⊥AD.∵SE∩EF=E,SE?平面SEF,EF?平面SEF,∴AD⊥平面SEF.
又AD?平面ABCD,∴平面SEF⊥平面ABCD.
故AD上存在中点E,使得平面SEF⊥平面ABCD.
(2)解法一
由(1)可知∠SEF就是二面角S-AD-B的平面角,∴∠SEF=120°.
以E为坐标原点,,的方向分别为x,y轴正方向,建立如图所示的空间直角坐标系E-xyz,
由△SAD为等腰直角三角形,,得,
.
可得,A(2,0,0),B(2,2,0),C(-2,2,0),∴,,,
设是平面SBC的法向量,
则即
可取.
设直线SA与平面SBC所成的角为θ,
则,∴直线SA与平面SBC所成角的正弦值为.
解法二
过点E作EG⊥SF于点G,由(1)知,AD⊥平面SEF,则BC⊥平面SEF,BC⊥EG,又SF∩BC=F,∴EG⊥平面SBC,易知AE∥平面SBC,则点A到平面SBC的距离等于EG.
由(1)可知∠SEF就是二面角S-AD-B的平面角,∴∠SEF=120°.
由△SAD为等腰直角三角形,,得,
.
又EF=AB=2,∴EG=1.
设直线SA与平面SBC所成的角为θ,
则
,
即直线SA与平面SBC所成角的正弦值为.
方法技巧
求解线段上点的位置的探索性问题,一般是先根据条件猜测点的位置,再给出证明,所求点多为中点或三等分点中某一个,也可以根据相似知识找点,求解时注意中位线的性质及三点共线条件的应用.
20.【试题情境】
本题是综合性、应用性、创新性题目,属于生活实践情境.
【关键能力】
本题考查数学建模能力、逻辑思维能力和创新能力.
【解题思路】
(1)由频率分布直方图与平均数计算公式求解即可.(2)(ⅰ)先利用频率分布直方图,求出随机抽取一名游客,该游客对景区不满意的概率,再利用相互独立事件的概率求解{am}的通项公式,最后利用等比数列的前n项和公式求解;(ⅱ)根据题意求出B1,B2及Bn与Bn-1,Bn-2(n≥3,n∈N
)的关系式,代入计算即可.
解:(1)这100名游客评分的平均值为
55×0.01+65×0.24+75×0.35+85×0.26+95×0.14=77.8(分).
(2)(ⅰ)由题得,
所以,
所以数列{am}的前4项和为.
(ⅱ)由题意得,,
则,则
.所以.
21.【关键能力】
本题考查逻辑思维能力、运算求解能力.
【学科素养】
试题以椭圆与圆为背景,很好地考查了考生对直线与圆相切的理解与应用,对三点共线的理解与应用,对方程思想与设而不求思想的应用,体现了理性思维、数学应用、数学探索学科素养.
【解题思路】(1)
(2)设直线l:y=k(x+1)关于x的一元二次方程
解:(1)因为圆的圆心为(-1,0),半径为,
所以椭圆C的左焦点F(-1,0),则c=1,a2-b2=1
①.
由圆与直线bx-ay=0相切,得
②,
由①②解得a=2,,
故椭圆C的标准方程为.
(2)由题意设直线l的方程为y=k(x+1).
由得(4k2+3)x2+8k2x+4k2-12=0.
设A(x1,y1),B(x2,y2),则,.
由得P,A′,B三点共线,所以直线PA,PB的斜率互为相反数.
又直线PA,PB的斜率分别为,,
所以,
所以x2y1+x1y2-m(y1+y2)=0,
所以x2k(x1+1)+x1k(x2+1)-m[k(x1+1)+k(x2+1)]=0,
所以2kx1x2+
k(x1+x2)-m[k(x1+x2)+2k]=0,
所以,
所以k(m+4)=0,
若k(m+4)=0对任意k∈R恒成立,则m=-4.
故在x轴上存在一个定点P(m,0),满足,且m的值为-4.
22.【必备知识】
本题考查的知识是能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,了解函数的单调性与导数的关系;能利用导数研究函数的单调性,会求函数的单调区间,会求闭区间上函数的最大值、最小值.
【关键能力】
本题考查逻辑思维能力、运算求解能力.
【解题思路】
(1)
(2)当a≤1,且a≠0时f(x)在[0,1]上单调递减x∈[0,1]时,
解:(1)由f(x)=ax-ex+2,得f′(x)=a-ex.
当a<0时,对任意x∈(-∞,+∞),f′(x)<0,所以f(x)单调递减.
当a>0时,令f′(x)=0,得x=ln
a,
当x∈(-∞,ln
a)时,f′(x)>0,当x∈(ln
a,+∞)时,f′(x)<0,
所以f(x)在(-∞,ln
a)上单调递增,在(ln
a,+∞)上单调递减.
综上所述,当a<0时,f(x)在(-∞,+∞)上单调递减;当a>0时,f(x)在(-∞,ln
a)上单调递增,在(ln
a,+∞)上单调递减.
(2)存在满足条件的实数a,且实数a的值为e+1.
理由如下:
①当a≤1,且a≠0时,由(1)知,f(x)在[0,1]上单调递减,
则x∈[0,1]时,f(x)max=f(0)=1,
则f(x1)+f(x2)≤2f(0)=2<4.
所以此时不满足题意.
②当1<a<e时,由(1)知,在[0,ln
a]上,f(x)单调递增,在(ln
a,1]上,f(x)单调递减,
则当x∈[0,1]时,f(x)max=f(ln
a)=aln
a-a+2.
当x1=0时,对任意x2∈[0,1],
f(x1)+f(x2)≤f(0)+f(ln
a)=1+aln
a-a+2=a(ln
a-1)+3<3.
所以此时不满足题意.
③当a≥e时,令g(x)=4-f(x)(x∈[0,1]),
由(1)知,f(x)在[0,1]上单调递增,进而知g(x)在[0,1]上单调递减,
所以g(x)max=g(0)=4-f(0),g(x)min=g(1)=4-f(1).
若对任意的x1∈[0,1],总存在x2∈[0,1],使得f(x1)+f(x2)=4,
则f(x1)=g(x2),即
所以f(0)+f(1)=a-e+3=4,解得a=e+1.
综上,存在满足题意的实数a,且实数a的值为e+1.
方法技巧
利用导数研究函数的单调性的一般步骤:①确定函数的定义域;②求导函数;③若求单调区间(或证明单调性),只需在函数的定义域内解(或证明)不等式f′(x)≥0或f′(x)≤0(不恒等于0)即可.
