【课件】1 勾股定理 第1课时 直角三角形三边的关系(共15张ppt)
文档属性
| 名称 | 【课件】1 勾股定理 第1课时 直角三角形三边的关系(共15张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览

文档简介
八年级数学上册(华东师大版)
A
B
C
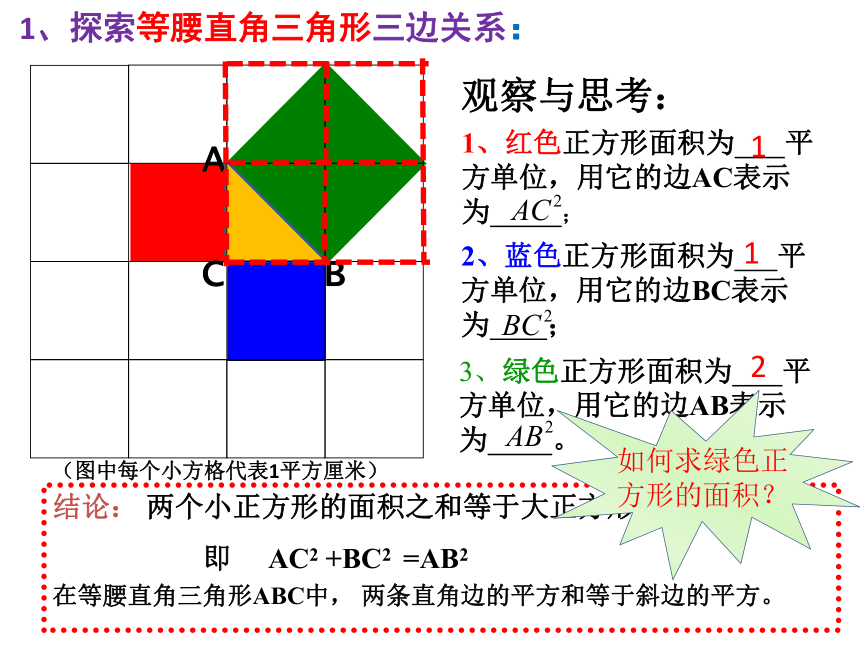
观察与思考:
1、红色正方形面积为 平方单位,用它的边AC表示为 ;
2、蓝色正方形面积为 平方单位,用它的边BC表示为 ;
3、绿色正方形面积为 平方单位,用它的边AB表示为 。
结论: 两个小正方形的面积之和等于大正方形的面积
即 AC2 +BC2 =AB2
在等腰直角三角形ABC中, 两条直角边的平方和等于斜边的平方。
1
2
1
如何求绿色正方形的面积?
1、探索等腰直角三角形三边关系:
(图中每个小方格代表1平方厘米)
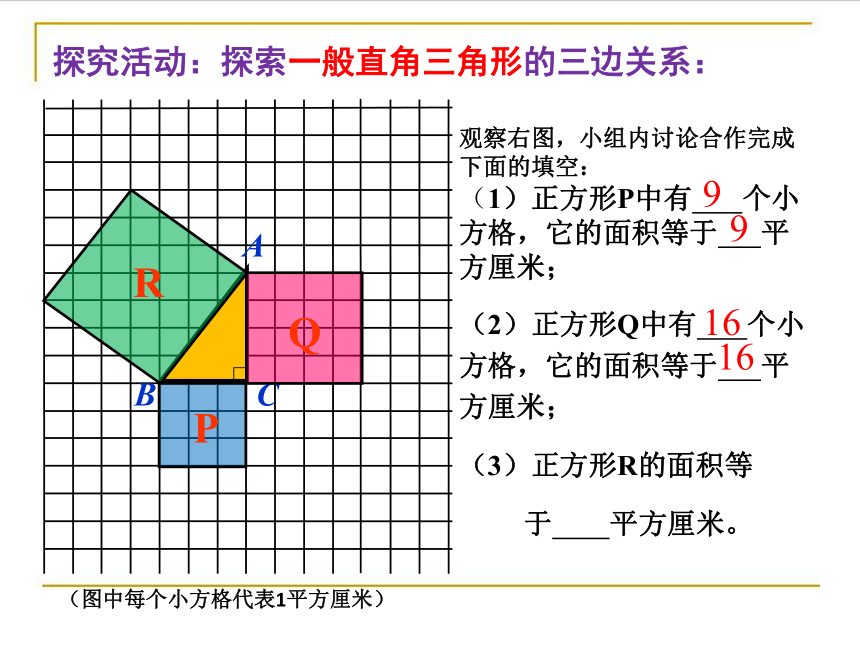
探究活动:探索一般直角三角形的三边关系:
C
A
B
观察右图,小组内讨论合作完成下面的填空:
(1)正方形P中有 个小方格,它的面积等于 平方厘米;
(2)正方形Q中有 个小方格,它的面积等于 平方厘米;
(3)正方形R的面积等
于 平方厘米。
P
R
Q
16
16
9
9
(图中每个小方格代表1平方厘米)
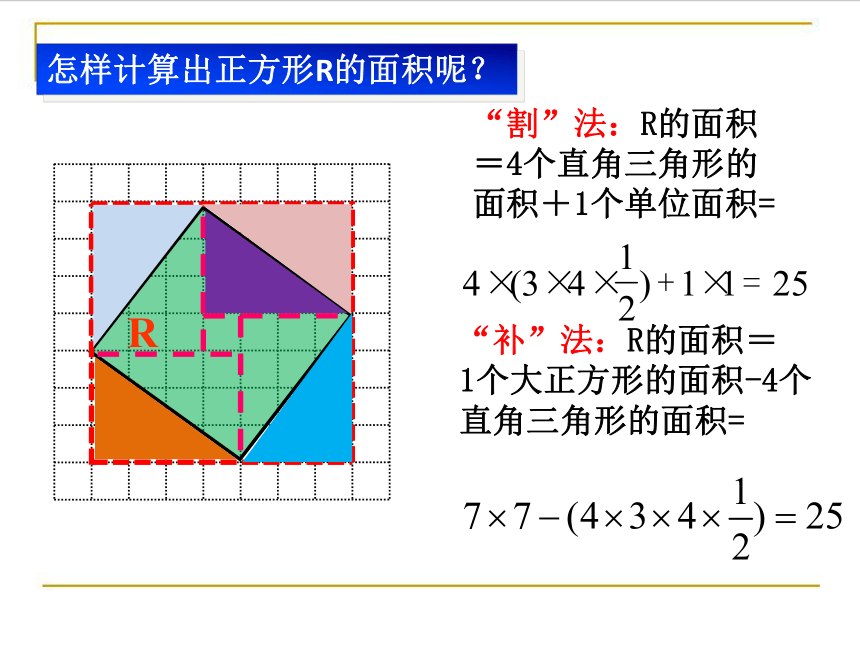
怎样计算出正方形R的面积呢?
R
“补”法:R的面积=
1个大正方形的面积-4个直角三角形的面积=
“割”法:R的面积=4个直角三角形的面积+1个单位面积=
Q
P
C
A
B
R
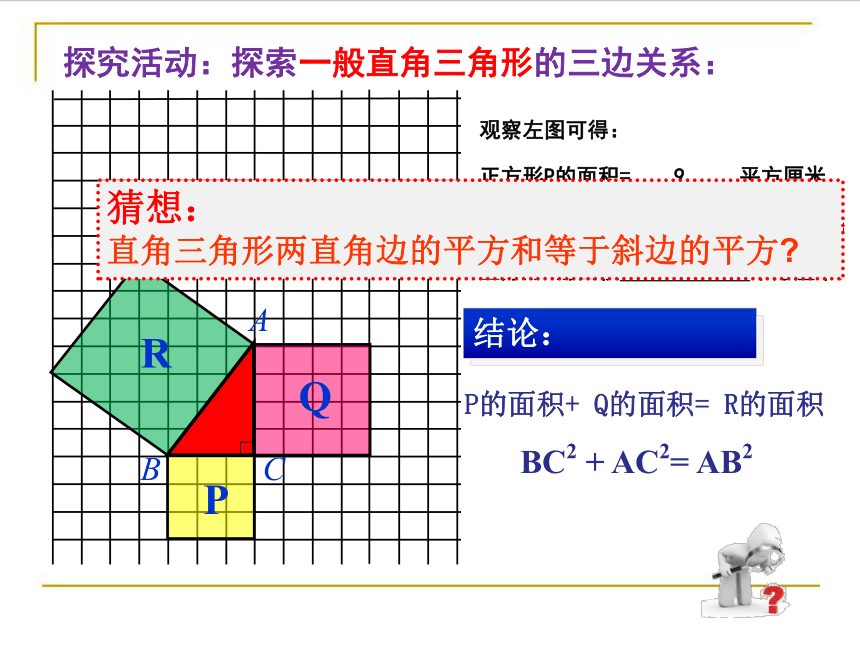
结论:
P的面积+ Q的面积= R的面积
BC2 + AC2= AB2
观察左图可得:
正方形P的面积= 9 平方厘米,
正方形Q的面积= 16 平方厘米;
正方形R的面积= 25 平方厘米;
猜想:
直角三角形两直角边的平方和等于斜边的平方?
探究活动:探索一般直角三角形的三边关系:
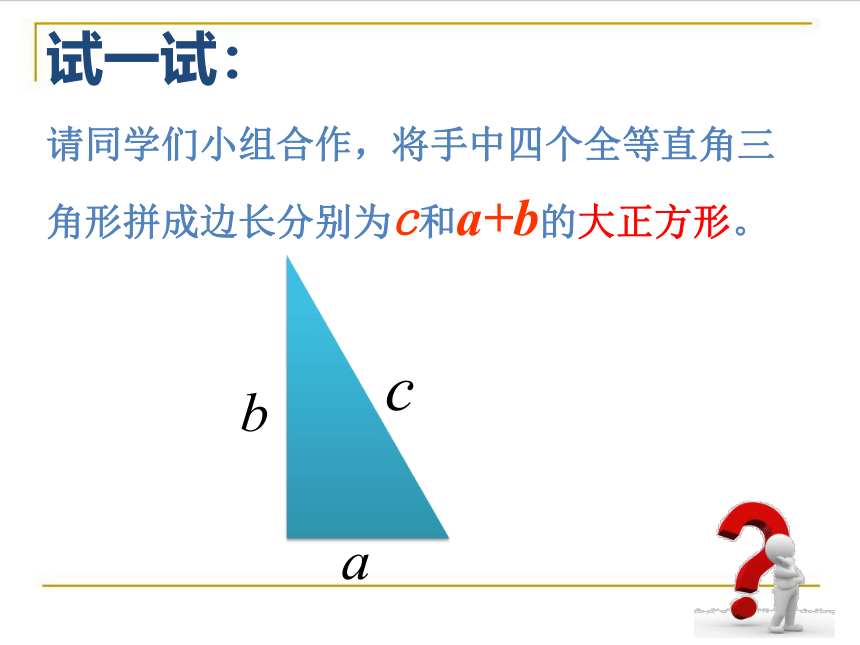
请同学们小组合作,将手中四个全等直角三角形拼成边长分别为c和a+b的大正方形。
试一试:
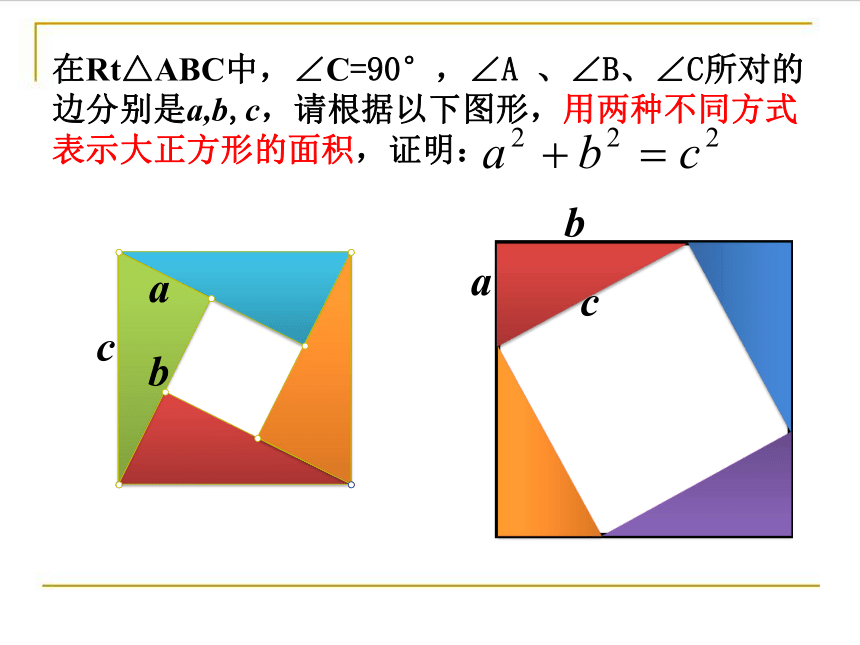
在Rt△ABC中,∠C=90°,∠A 、∠B、∠C所对的
边分别是a,b,c,请根据以下图形,用两种不同方式
表示大正方形的面积,证明:
b
a
c
b
a
c
证明(一):
“弦图”
直角三角形两直角边的平方和等于斜边的平方
大正方形的面积=小正方形面积+4个直角三角形面积
b
a
c
证明(二)
直角三角形两直角边的平方和等于斜边的平方
大正方形的面积=小正方形面积+4个直角三角形面积
b
a
c
a
b
c
c
c
a
b
b
a
即:在Rt△ABC中,∠C=90°,那么:
b
c
a
C
A
B
勾股定理:
直角三角形两直角边的平方和等于斜边的平方.
勾股定理的各种表达式:
在RT△ABC中,∠C=90°, ∠A 、∠B、 ∠C的对边分别为a 、b 、c ,则:
b
c
a
C
A
B
知识应用
例1:在Rt△ABC中,已∠B=90°,AB=6,BC =8,求AC的长度。
A
B
C
6
8
解:在Rt△ABC中,∠B=90° ,
根据勾股定理可得:
AC=10
答:AC的长度是10。
用一用
1.在△ABC中,∠C=90°.
(1)若a=6,c=10,则b= ;
(2)若c=25,b=24,则a= ;
2.已知直角三角形ABC的两边为3和4,求第三边c.
一个定理
感悟收获
一种思想
一次探究
一种方法
一份自豪
1.必做题:同步练习册14.1.1
2.选做题:
(1)课本第118页“阅读与思考”,了解勾股定理的多种证法.
(2)上网查阅了解勾股定理的有关知识并写一篇小论文.
课后作业
说不定你也可以创造一种新的证明方法呢!
A
B
C
观察与思考:
1、红色正方形面积为 平方单位,用它的边AC表示为 ;
2、蓝色正方形面积为 平方单位,用它的边BC表示为 ;
3、绿色正方形面积为 平方单位,用它的边AB表示为 。
结论: 两个小正方形的面积之和等于大正方形的面积
即 AC2 +BC2 =AB2
在等腰直角三角形ABC中, 两条直角边的平方和等于斜边的平方。
1
2
1
如何求绿色正方形的面积?
1、探索等腰直角三角形三边关系:
(图中每个小方格代表1平方厘米)
探究活动:探索一般直角三角形的三边关系:
C
A
B
观察右图,小组内讨论合作完成下面的填空:
(1)正方形P中有 个小方格,它的面积等于 平方厘米;
(2)正方形Q中有 个小方格,它的面积等于 平方厘米;
(3)正方形R的面积等
于 平方厘米。
P
R
Q
16
16
9
9
(图中每个小方格代表1平方厘米)
怎样计算出正方形R的面积呢?
R
“补”法:R的面积=
1个大正方形的面积-4个直角三角形的面积=
“割”法:R的面积=4个直角三角形的面积+1个单位面积=
Q
P
C
A
B
R
结论:
P的面积+ Q的面积= R的面积
BC2 + AC2= AB2
观察左图可得:
正方形P的面积= 9 平方厘米,
正方形Q的面积= 16 平方厘米;
正方形R的面积= 25 平方厘米;
猜想:
直角三角形两直角边的平方和等于斜边的平方?
探究活动:探索一般直角三角形的三边关系:
请同学们小组合作,将手中四个全等直角三角形拼成边长分别为c和a+b的大正方形。
试一试:
在Rt△ABC中,∠C=90°,∠A 、∠B、∠C所对的
边分别是a,b,c,请根据以下图形,用两种不同方式
表示大正方形的面积,证明:
b
a
c
b
a
c
证明(一):
“弦图”
直角三角形两直角边的平方和等于斜边的平方
大正方形的面积=小正方形面积+4个直角三角形面积
b
a
c
证明(二)
直角三角形两直角边的平方和等于斜边的平方
大正方形的面积=小正方形面积+4个直角三角形面积
b
a
c
a
b
c
c
c
a
b
b
a
即:在Rt△ABC中,∠C=90°,那么:
b
c
a
C
A
B
勾股定理:
直角三角形两直角边的平方和等于斜边的平方.
勾股定理的各种表达式:
在RT△ABC中,∠C=90°, ∠A 、∠B、 ∠C的对边分别为a 、b 、c ,则:
b
c
a
C
A
B
知识应用
例1:在Rt△ABC中,已∠B=90°,AB=6,BC =8,求AC的长度。
A
B
C
6
8
解:在Rt△ABC中,∠B=90° ,
根据勾股定理可得:
AC=10
答:AC的长度是10。
用一用
1.在△ABC中,∠C=90°.
(1)若a=6,c=10,则b= ;
(2)若c=25,b=24,则a= ;
2.已知直角三角形ABC的两边为3和4,求第三边c.
一个定理
感悟收获
一种思想
一次探究
一种方法
一份自豪
1.必做题:同步练习册14.1.1
2.选做题:
(1)课本第118页“阅读与思考”,了解勾股定理的多种证法.
(2)上网查阅了解勾股定理的有关知识并写一篇小论文.
课后作业
说不定你也可以创造一种新的证明方法呢!
