人教版必修一第三章《相互作用》课件研究物体间的相互作用
文档属性
| 名称 | 人教版必修一第三章《相互作用》课件研究物体间的相互作用 |  | |
| 格式 | rar | ||
| 文件大小 | 313.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-11-16 18:33:03 | ||
图片预览








文档简介
(共42张PPT)
第三章 研究物体间的相互作用
弹力
两个接触的物体之间由于形变而产生的力
弹力产生的条件
1、直接接触
2、发生弹性形变
弹力的大小:
为劲度系数
单位:N/m
胡克定律:
弹力的方向
支持力:垂直于接触面,指向被支持的物体
弹力的方向
压力:垂直于接触面,指向被压物体
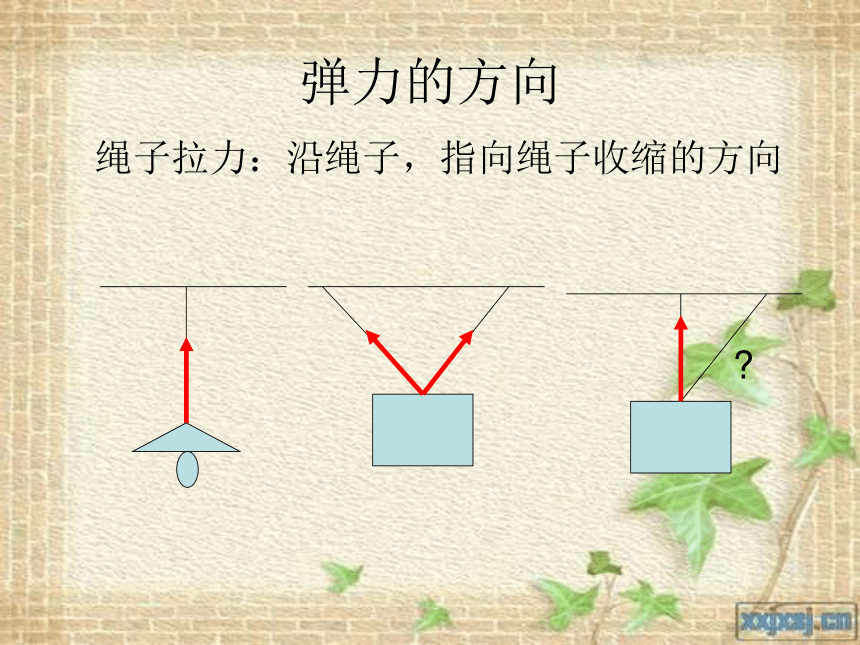
弹力的方向
绳子拉力:沿绳子,指向绳子收缩的方向
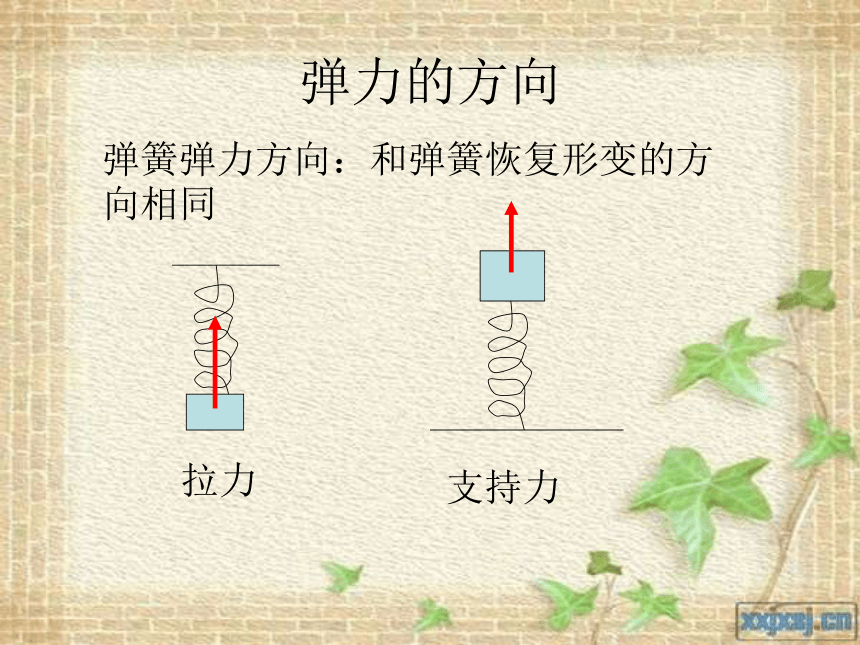
弹力的方向
弹簧弹力方向:和弹簧恢复形变的方向相同
拉力
支持力
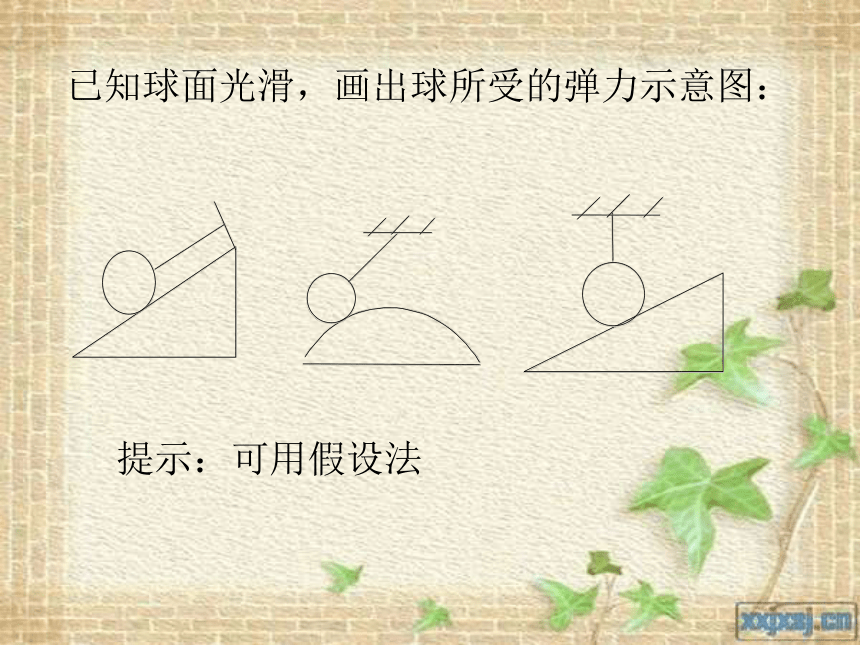
已知球面光滑,画出球所受的弹力示意图:
提示:可用假设法
滑动摩擦力
产生条件:
接触面粗糙
有相对运动
接触且挤压
大小:
为动摩擦因数
为物体与接触面的正压力,大小等于物体受到的支持力
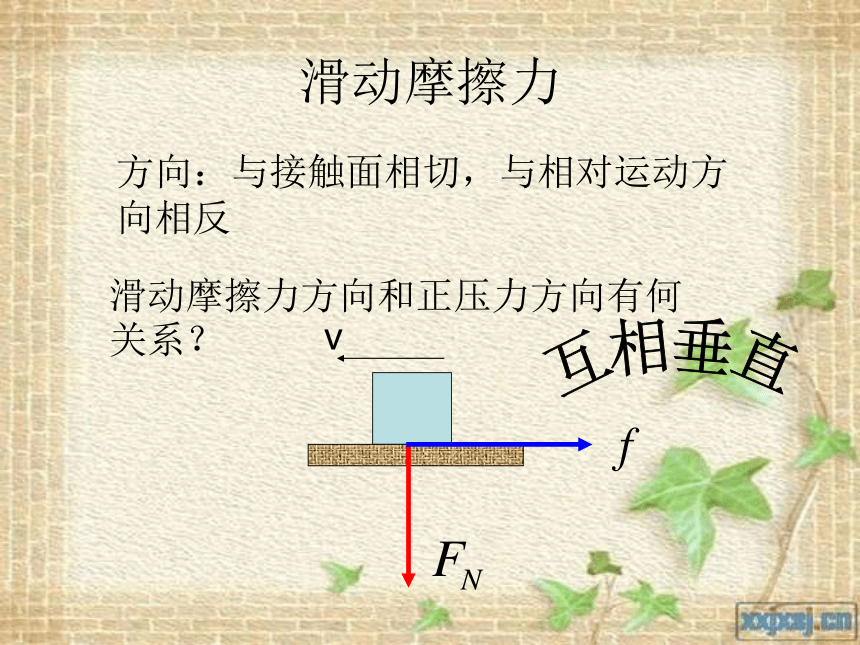
滑动摩擦力
方向:与接触面相切,与相对运动方 向相反
滑动摩擦力方向和正压力方向有何关系?
v
静摩擦力
产生条件:
接触且挤压
有相对运动趋势
接触面粗糙
大小:
为最大静摩擦力,与压力有关,有时可认为等于滑动摩擦力
静摩擦力
方向:与接触面相切,与相对运动趋势的方向相反
相对运动趋势的方向就是当接触面光滑的时候物体的运动方向
若较难判断,一般用假设法
摩擦力概念的理解
关于静摩擦力,下列说法中正确的是( )
A.静摩擦力的方向一定与物体的运动方向相反
B.静止物体所受的静摩擦力一定为零
C.两个物体之间的静摩擦力总是一个定值
D.运动的物体可能受静摩擦力的作用
一放在水平桌子上的木块在水平方向上受到
两个力的作用,处于静止状态。其中F1=10N,
F2=2N。若撤去F1,则木块受到的摩擦力大小
和方向,木块受到的合力为
A、8N,方向向右;6N
F1
F2
B、6N,方向向右;0
C、2N,方向向右;0
D、0;0
质量为2kg的物体,静止在水平地面上,物体与地面间的动摩擦因数为0.5,最大静摩擦力与滑动摩擦力大小视为相等,给物体施加以水平拉力,试求:
(1)当拉力大小为5N时,地面对物体的摩擦力是多大?
(2)当拉力大小变为12N时,地面对物体的摩擦力是多大?
(3)此后,若将拉力又减小为5N(物体仍在滑动),地面对物体的摩擦力是多大?
(4)若将此物体用12N的水平力压在平整的竖直墙上,动摩擦因数仍为0.5,墙壁对物体的摩擦力为多大?
力的合成
同一直线上的力的合成是代数运算,可以直接相加减,同向相加,反向相减
的正负表示力的方向
力的合成
互成角度的两个力的合成遵循平行四边形定则
合成方法有三种:
作图法、公式法、正交分解法
合力大小的范围
配套练习P123.2
力的合成 作图法
做出两个分力的图示
以表示这两个分力的线段为邻边画出平行四边形,并连接两邻边所夹对角线
用刻度尺量出对角线长度,根据所定标度求出合力大小
用量角器量出合力与一个分力的夹角表示合力的方向
力的合成 作图法
5N
力的合成 公式法
两种常见情况
1、互相垂直的两个力的合成
力的合成 公式法
2、两个等大的力的合成
平行四边形为菱形,对角线互相垂直平分
力的合成 公式法
2、两个等大的力的合成
当两力夹角为
合力等于分力大小
所以,随着夹角的增大,合力减小
力的合成 ——正交分解法
把力沿着两个互相垂直的方向分解,多用于求三个或三个以上力的合力
正交分解法求合力的步骤:
1、建立合适的坐标系
2、分解不在轴上的力
3、分求两坐标轴上的合力
4、根据勾股定理求总合力
5、再求角度表方向
力的合成 正交分解法
x
y
X方向合力:
y方向合力:
与x轴夹角
力的分解
按作用效果分解
G
G
力的分解
物体的平衡
平衡状态
静止
匀速直线运动
a=0
共点力的平衡条件:合外力为0
处于平衡状态的物体如果保持其它力不变,突然撤去某一个力,则物体所受的合力必然与撤去的力大小相等方向相反
物体受到四个力的作用处于静止状态,当减少5N时,物体所受合外力为多少?方向如何?
解决共点力平衡问题的一般步骤
选取研究对象
对所选取的对象进行受力分析,画出受力示意图
采用合成法、分解法或正交分解法对所受的力进行处理
根据平衡条件列方程,对各分力或合力回到平行四边形中进行求解
求解方程
求解平衡问题常用方法
合成法
分解法
正交分解法
合成法
解题依据:物体受三个力平衡时,其中两个力的合力和第三个力等大反向
G
G
合成法应用
求OA和OB绳受到的弹力
O
A
B
分解法
解题依据:物体受三个力平衡时,可将任意一个力沿着其它两个力的反方向分解,则物体相当于受到两对平衡力的作用.两个分力通过三角形知识求解
G
分解法应用
金属球放在光滑的斜面上,用垂直于斜面的挡板挡住,如图,求斜面和挡板受到的作用力
G
正交分解法
解题依据:将所有的力分解到两个互相垂直的坐标轴上,每个坐标轴上的合力为零
正交分解法多用于求3个以上共点力的平衡问题
正交分解法应用
G
x
y
由平衡条件知:
由几何知识有:
联立解得:
三种方法的共同点
无论是合成还是分解都遵循平行四边形定则,求合力或分力都要回到平行四边形当中,一般利用三角函数关系求解
G
G
G
x
三角函数知识
A
B
C
三角函数知识
一些特殊的三角函数值:
练习
1、如图1,用与水平方向成 的力F将质量为m的物体沿着墙面匀速向上推,墙与物体间的动摩擦因数为 ,求物体对墙的压力及墙与物体之间的摩擦力。
F
图1
2、质量为m的物体置于粗糙水平面上,物体与水平面间的动摩擦因数为 ,用与水平方向成 的力F匀速向右拉动物体,试求F的大小。
F
3、《配套自主学案》P126 9
F
第三章 研究物体间的相互作用
弹力
两个接触的物体之间由于形变而产生的力
弹力产生的条件
1、直接接触
2、发生弹性形变
弹力的大小:
为劲度系数
单位:N/m
胡克定律:
弹力的方向
支持力:垂直于接触面,指向被支持的物体
弹力的方向
压力:垂直于接触面,指向被压物体
弹力的方向
绳子拉力:沿绳子,指向绳子收缩的方向
弹力的方向
弹簧弹力方向:和弹簧恢复形变的方向相同
拉力
支持力
已知球面光滑,画出球所受的弹力示意图:
提示:可用假设法
滑动摩擦力
产生条件:
接触面粗糙
有相对运动
接触且挤压
大小:
为动摩擦因数
为物体与接触面的正压力,大小等于物体受到的支持力
滑动摩擦力
方向:与接触面相切,与相对运动方 向相反
滑动摩擦力方向和正压力方向有何关系?
v
静摩擦力
产生条件:
接触且挤压
有相对运动趋势
接触面粗糙
大小:
为最大静摩擦力,与压力有关,有时可认为等于滑动摩擦力
静摩擦力
方向:与接触面相切,与相对运动趋势的方向相反
相对运动趋势的方向就是当接触面光滑的时候物体的运动方向
若较难判断,一般用假设法
摩擦力概念的理解
关于静摩擦力,下列说法中正确的是( )
A.静摩擦力的方向一定与物体的运动方向相反
B.静止物体所受的静摩擦力一定为零
C.两个物体之间的静摩擦力总是一个定值
D.运动的物体可能受静摩擦力的作用
一放在水平桌子上的木块在水平方向上受到
两个力的作用,处于静止状态。其中F1=10N,
F2=2N。若撤去F1,则木块受到的摩擦力大小
和方向,木块受到的合力为
A、8N,方向向右;6N
F1
F2
B、6N,方向向右;0
C、2N,方向向右;0
D、0;0
质量为2kg的物体,静止在水平地面上,物体与地面间的动摩擦因数为0.5,最大静摩擦力与滑动摩擦力大小视为相等,给物体施加以水平拉力,试求:
(1)当拉力大小为5N时,地面对物体的摩擦力是多大?
(2)当拉力大小变为12N时,地面对物体的摩擦力是多大?
(3)此后,若将拉力又减小为5N(物体仍在滑动),地面对物体的摩擦力是多大?
(4)若将此物体用12N的水平力压在平整的竖直墙上,动摩擦因数仍为0.5,墙壁对物体的摩擦力为多大?
力的合成
同一直线上的力的合成是代数运算,可以直接相加减,同向相加,反向相减
的正负表示力的方向
力的合成
互成角度的两个力的合成遵循平行四边形定则
合成方法有三种:
作图法、公式法、正交分解法
合力大小的范围
配套练习P123.2
力的合成 作图法
做出两个分力的图示
以表示这两个分力的线段为邻边画出平行四边形,并连接两邻边所夹对角线
用刻度尺量出对角线长度,根据所定标度求出合力大小
用量角器量出合力与一个分力的夹角表示合力的方向
力的合成 作图法
5N
力的合成 公式法
两种常见情况
1、互相垂直的两个力的合成
力的合成 公式法
2、两个等大的力的合成
平行四边形为菱形,对角线互相垂直平分
力的合成 公式法
2、两个等大的力的合成
当两力夹角为
合力等于分力大小
所以,随着夹角的增大,合力减小
力的合成 ——正交分解法
把力沿着两个互相垂直的方向分解,多用于求三个或三个以上力的合力
正交分解法求合力的步骤:
1、建立合适的坐标系
2、分解不在轴上的力
3、分求两坐标轴上的合力
4、根据勾股定理求总合力
5、再求角度表方向
力的合成 正交分解法
x
y
X方向合力:
y方向合力:
与x轴夹角
力的分解
按作用效果分解
G
G
力的分解
物体的平衡
平衡状态
静止
匀速直线运动
a=0
共点力的平衡条件:合外力为0
处于平衡状态的物体如果保持其它力不变,突然撤去某一个力,则物体所受的合力必然与撤去的力大小相等方向相反
物体受到四个力的作用处于静止状态,当减少5N时,物体所受合外力为多少?方向如何?
解决共点力平衡问题的一般步骤
选取研究对象
对所选取的对象进行受力分析,画出受力示意图
采用合成法、分解法或正交分解法对所受的力进行处理
根据平衡条件列方程,对各分力或合力回到平行四边形中进行求解
求解方程
求解平衡问题常用方法
合成法
分解法
正交分解法
合成法
解题依据:物体受三个力平衡时,其中两个力的合力和第三个力等大反向
G
G
合成法应用
求OA和OB绳受到的弹力
O
A
B
分解法
解题依据:物体受三个力平衡时,可将任意一个力沿着其它两个力的反方向分解,则物体相当于受到两对平衡力的作用.两个分力通过三角形知识求解
G
分解法应用
金属球放在光滑的斜面上,用垂直于斜面的挡板挡住,如图,求斜面和挡板受到的作用力
G
正交分解法
解题依据:将所有的力分解到两个互相垂直的坐标轴上,每个坐标轴上的合力为零
正交分解法多用于求3个以上共点力的平衡问题
正交分解法应用
G
x
y
由平衡条件知:
由几何知识有:
联立解得:
三种方法的共同点
无论是合成还是分解都遵循平行四边形定则,求合力或分力都要回到平行四边形当中,一般利用三角函数关系求解
G
G
G
x
三角函数知识
A
B
C
三角函数知识
一些特殊的三角函数值:
练习
1、如图1,用与水平方向成 的力F将质量为m的物体沿着墙面匀速向上推,墙与物体间的动摩擦因数为 ,求物体对墙的压力及墙与物体之间的摩擦力。
F
图1
2、质量为m的物体置于粗糙水平面上,物体与水平面间的动摩擦因数为 ,用与水平方向成 的力F匀速向右拉动物体,试求F的大小。
F
3、《配套自主学案》P126 9
F
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
