2020-2021学年北师大版七年级数学上册第五章一元一次方程单元必刷 试卷(word版含答案解析)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学上册第五章一元一次方程单元必刷 试卷(word版含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 445.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览



文档简介
第五章一元一次方程单元必刷
一、选择题(48分)
(2019·期末·江苏苏州市高新区)某服装进货价
元/件,标价为
元/件,商店将此服装打
折销售后仍获利
,则
为
A.
B.
C.
D.
(2019·期末·广东深圳市福田区)如图,正方形
的轨道上有两个点甲与乙,开始时甲在
处,乙在
处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒
,乙的速度为每秒
,已知正方形轨道
的边长为
,则乙在第
次追上甲时的位置在
A.
上
B.
上
C.
上
D.
上
(2019·期末·广东惠州市惠阳区)在解方程
时,去分母后正确的是
A.
B.
C.
D.
(2019·期末·河北石家庄市高邑县)某商店把一件商品按进价增加
作为定价,可是总卖不出去,后来老板把定价降低
,以
元的价格出售,很快就卖出了,则老板卖出这件商品的盈亏情况是
A.亏
元
B.亏
元
C.赚
元
D.不亏不赚
(2019·期中·广东广州市南沙区)若
,
是有理数,下列说法:①若
,则
;②若
,则
;③若
,则
;④若
,则
;⑤若
,则
.其中正确的有
A.
个
B.
个
C.
个
D.
个
(2019·期中·福建厦门市思明区)我国古代数学名著《孙子算经》中记载了一道题,大意是:
匹马拉了
片瓦,已知
匹大马能拉
片瓦,
匹小马能拉
片瓦,问多少匹大马、多少匹小马?若设大马有
匹,那么可列方程为
A.
B.
C.
D.
(2019·期末·陕西西安市雁塔区)在甲处工作的有
人,在乙处工作的有
人,如果要使乙处工作的人数是甲处工作人数的
,应从乙处调多少人到甲处,若设应从乙处调
人到甲处,则下列方程中正确的是
A.
B.
C.
D.
(2020·同步练习)对有理数
,
定义新运算“”:规定
.若
,则
的值为
A.
B.
C.
D.
(2019·期末·天津天津市红桥区)把方程
的分母化为整数后的方程是
A.
B.
C.
D.
(2019·期中·北京北京市朝阳区)
中,
厘米,,
厘米,点
为
的中点.如果点
在线段
上以
厘米/秒的速度由
点向
点运动,同时,点
在线段
上由
点向
点运动.若点
的运动速度为
厘米/秒,则当
与
全等时,
的值为
A.
B.
C.
或
D.
或
(2019·期中·天津天津市红桥区)已知
,,且
,则
的值为
A.
B.
C.
或
D.
或
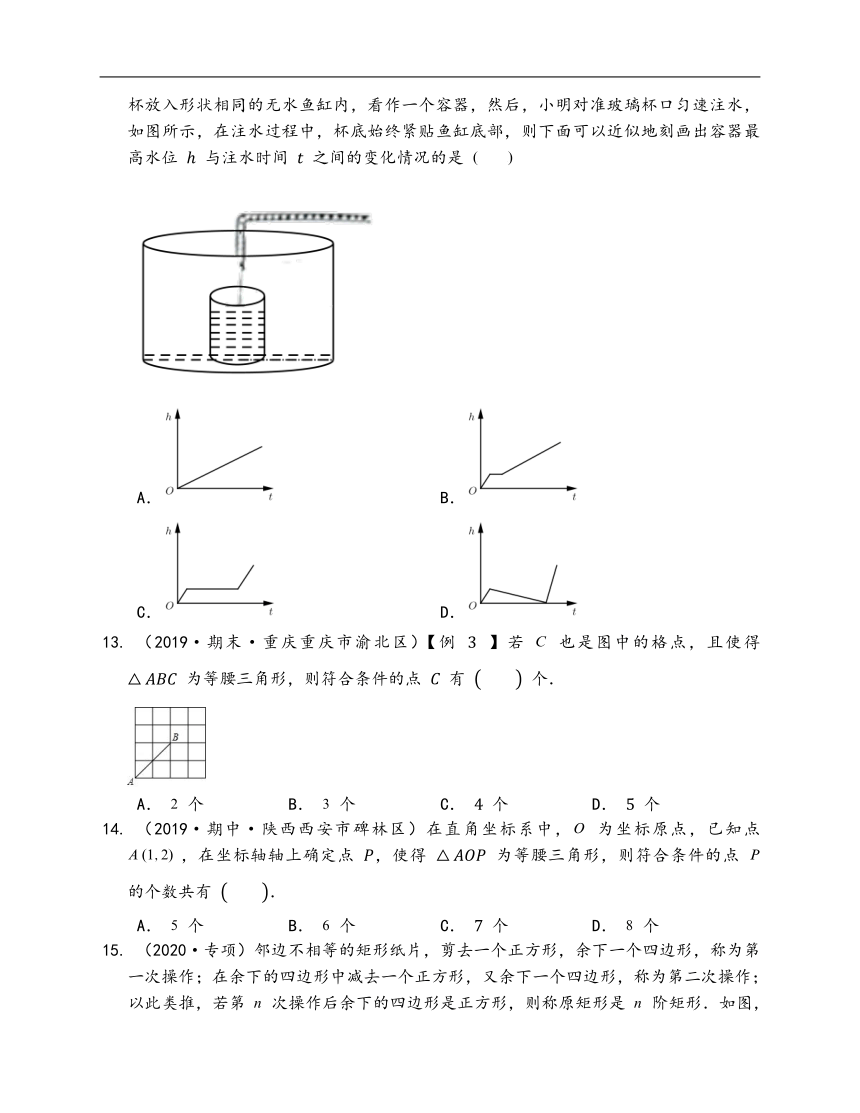
(2019·期中·山东青岛市市南区)小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位
与注水时间
之间的变化情况的是
A.
B.
C.
D.
(2019·期末·重庆重庆市渝北区)【例
】若
也是图中的格点,且使得
为等腰三角形,则符合条件的点
有
个.
A.
个
B.
个
C.
个
D.
个
(2019·期中·陕西西安市碑林区)在直角坐标系中,
为坐标原点,已知点
,在坐标轴轴上确定点
,使得
为等腰三角形,则符合条件的点
的个数共有
.
A.
个
B.
个
C.
个
D.
个
(2020·专项)邻边不相等的矩形纸片,剪去一个正方形,余下一个四边形,称为第一次操作;在余下的四边形中减去一个正方形,又余下一个四边形,称为第二次操作;以此类推,若第
次操作后余下的四边形是正方形,则称原矩形是
阶矩形.如图,矩形
中,若
,,则矩形
是
阶矩形.已知一个矩形是
阶矩形,较短边长为
,则较长边的长度为
A.
B.
C.
或
D.
或
(2019·期中·吉林长春市朝阳区)已知等腰三角形的两边长
,
满足方程组
则此等腰三角形的周长为
A.
B.
C.
D.
或
二、填空题(18分)
(2018·期末·广东佛山市禅城区)如图,小红将一个正方形纸片剪去一个宽为
的长条后,再从剩下的长方形纸片上剪去一个宽为
的长条,且剪下的两个长条的面积相等.问这个正方形的边长应为多少厘米?设正方形边长为
,则可列方程为
.
(2020·期末·四川绵阳市涪城区)已知:,,,且
到
轴距离为
,则点
的坐标是
.
(2019·期中·北京北京市西城区)若
,则
的值为
.
(2019·期末·呼和浩特市)一元一次方程
的解是
.
(2018·期中·辽宁大连市西岗区)在平面直角坐标系中,已知点
,,以原点
为位似中心,相似比为
,把
缩小为
,则点
的对应点
的坐标是
.
(2020·期末·四川绵阳市涪城区)已知正整数
,,
满足
,,则
.
(2018·期末·甘肃兰州市城关区)如图,长方体的长为
,宽为
,高为
,点
离点
的距离为
,一只蚂蚁如果要沿着长方体的表面从点
爬到点
,需要爬行的最短距离是
.
三、解答题(56分)
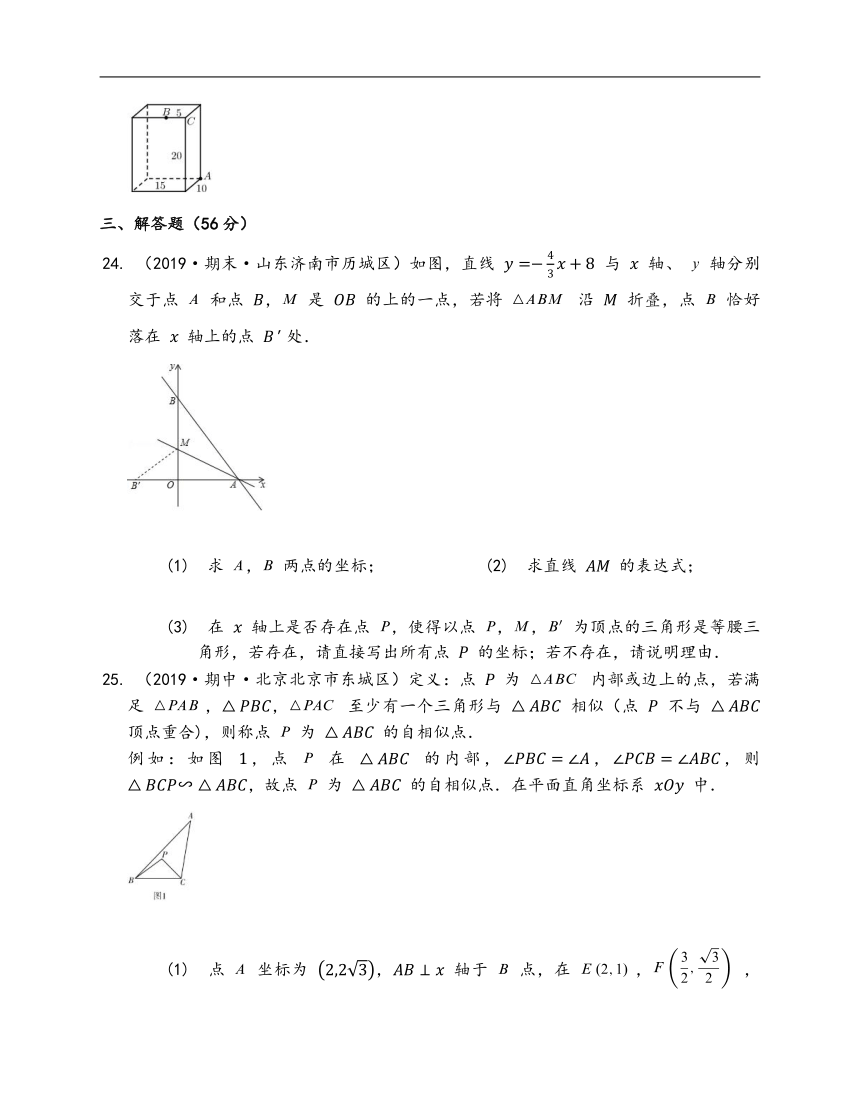
(2019·期末·山东济南市历城区)如图,直线
与
轴、
轴分别交于点
和点
,
是
的上的一点,若将
沿
折叠,点
恰好落在
轴上的点
处.
(1)
求
,
两点的坐标;
(2)
求直线
的表达式;
(3)
在
轴上是否存在点
,使得以点
,,
为顶点的三角形是等腰三角形,若存在,请直接写出所有点
的坐标;若不存在,请说明理由.
(2019·期中·北京北京市东城区)定义:点
为
内部或边上的点,若满足
,,
至少有一个三角形与
相似(点
不与
顶点重合),则称点
为
的自相似点.
例如:如图
,点
在
的内部,,,则
,故点
为
的自相似点.在平面直角坐标系
中.
(1)
点
坐标为
,
轴于
点,在
,,
这三个点中,其中是
自相似点的是
(填字母);
(2)
若点
是曲线
上的一个动点,
为
轴正半轴上一个动点;
①如图
,,
点横坐标为
,且
,若点
是
的自相似点,求点
的坐标;
②若
,点
为
,且
的自相似点有
个,则曲线
上满足这样条件的点
共有
个,请在图
中画出这些点(保留必要的画图痕迹).
(2019·期末·江苏苏州市姑苏区)解下列方程:
(1)
;
(2)
.
(2018·期末·云南昆明市官渡区)已知数轴上三点
,,
对应的数分别为
,,,点
为数轴上任意点,其对应的数为
.
(1)
的长为
.
(2)
如果点
到点
,点
的距离相等,那么
的值是:
.
(3)
如果点
以每分钟
个单位长度的速度从点
向左运动,同时点
和点
分别以每分钟
个单位长度和每分钟
个单位长度的速度也向左运动,设
分钟时点
到点
,点
的距离相等,求
的值.
答案
一、选择题
1.
【答案】B
【解析】根据题意得:,
解得:.
【知识点】利润问题
2.
【答案】D
【解析】设乙走
秒第一次追上甲.
根据题意,得
,
解得
.
乙走
秒第一次追上甲,则乙在第
次追上甲时的位置是
上;
设乙再走
秒第二次追上甲.
根据题意,得
,解得
.
乙再走
秒第二次追上甲,则乙在第
次追上甲时的位置是
上;
同理:
乙再走
秒第三次次追上甲,则乙在第
次追上甲时的位置是
上;
乙再走
秒第四次追上甲,则乙在第
次追上甲时的位置是
上;
乙在第
次追上甲时的位置又回到
上;
,
乙在第
次追上甲时的位置是
上.
【知识点】行程问题、用代数式表示规律
3.
【答案】D
【解析】去分母得:.
【知识点】去分母
去括号
4.
【答案】A
【解析】设商品进价为
,根据题意得:
解得
,
以
元出售,可见亏
元.
【知识点】利润问题
5.
【答案】B
【解析】①若
,则
不一定小于
,如
,,故①错误;
②若
,则
不一定大于
,如
,,故②错误;
③若
,则
,故③正确;
④若
,则
可能等于
,如
,,,故④错误;
⑤若
,则
,故⑤正确,
正确的有③和⑤,一共
个.
故选B.
【知识点】利用绝对值比较数的大小
6.
【答案】D
【解析】设大马有
匹,则小马有
匹,
由题意,得
.
【知识点】和差倍分
7.
【答案】D
【解析】设应从乙处调
人到甲处,
则甲处现有的工作人数为
人,
乙处现有的工作人数为
人.
根据“乙处工作的人数是甲处工作人数的
,”
列方程得:.
【知识点】和差倍分
8.
【答案】D
【知识点】去分母
去括号
9.
【答案】D
【知识点】去分母
去括号
10.
【答案】C
【知识点】边角边
11.
【答案】D
【解析】
,
,
,
,
又
,由于
,,而
,,
则
只能取
,
取
或
,
或
.
则
的值为
或
.
【知识点】绝对值的性质
12.
【答案】B
【解析】一注水管向小玻璃杯内注水,水面在逐渐升高,当小杯中水满时,开始向大桶内流,这时水位高度不变.当桶内水面高度与小杯一样后,再继续注水,水面高度在升高,升高的比开始变慢.
【知识点】用函数图象表示实际问题中的函数关系
13.
【答案】C
【解析】如图:
分情况讨论.
①
为等腰
底边时,符合条件的
点有
个;
②
为等腰
其中的一条腰时,符合条件的
点有
个.
故选:C.
【知识点】垂直平分线的性质、等腰三角形的概念
14.
【答案】D
【解析】根据已知线段构造等腰三角形.
①以
为圆心,以
为半径作圆,交于坐标轴两点;
②以
为圆心,以
为半径作圆,此时交坐标轴四个点;
③作线段
垂直平分线,交坐标轴两个点,共
个点.
【知识点】等腰三角形的概念
15.
【答案】D
【知识点】矩形的性质、正方形的性质
16.
【答案】A
【解析】
解不等式组可得
等腰三角形的两边长为
,,
三边可能情况为
,,
或
,,,
,,
不能构成三角形,
等腰三角形的周长为
.
【知识点】等腰三角形的概念
二、填空题
17.
【答案】
;
【解析】设正方形边长为
,
由题意得:,
故答案为:.
【知识点】几何问题
18.
【答案】
或
;
【解析】因为
,
所以
,
因为点
到
轴距离为
,
所以
,
所以点
的坐标为
或
.
【知识点】连线与坐标轴平行的两点间距离
19.
【答案】
或
;
【解析】
,
,
.
【知识点】含绝对值的一元一次方程的解法
20.
【答案】
;
【解析】去分母得:,
移项得:,
合并同类项得:,
系数化为
得:.
故答案为:.
【知识点】去分母
去括号
21.
【答案】
或
;
【解析】
点
,以原点
为位似中心,相似比为
,把
缩小,
对应点都乘以
或
,
则点
的对应点坐标为
或
.
【知识点】位似图形的性质应用
22.
【答案】
;
【解析】由题
由②知:,
,,
均为正整数,即
,,
且为整数,
为偶数且
,,
①
,,代入①,②,
即
故
,,,
此时
;
②
时,
代入①,②,
即
不满足;
③
时,,
即
此时解出
不满足,
继续变大时,解出的
更小,
故仅
,,
满足,
.
故答案为:.
【知识点】代入消元法转为二元一次方程(组)
23.
【答案】
;
【解析】三种情况:
由于
,故最短距离为
.
【知识点】平面展开-最短路径问题
三、解答题
24.
【答案】
(1)
当
时,,
,
当
时,,,
.
(2)
在
中,,,,
,
由折叠得:,
,
设
,则
,
由勾股定理得:,,
,
设
,
则
解得:
直线
的解析式为:.
(3)
点的坐标为
或
或
或
.
【解析】
(3)
在
轴上存在点
,使得以点
,,
为顶点的三角形是等腰二角形,如图.
,,
,
当
时,,;
当
时,,
当
时,作
的垂直平分线,交
轴于
,交
与
,连接
,
设
,则
,
,
,解得
,
.
综上,
点的坐标为
或
或
或
.
【知识点】一次函数的解析式、一次函数与三角形的综合、等腰三角形的判定
25.
【答案】
(1)
(2)
①如图
,过点
作
轴于
点.
点的横坐标为
,
,
,
,,,
直线
的表达式为
,
在
中,,,
设
,则
,
,
,
,,
,,
,
是等边三角形,
,
的横坐标为
,
的横坐标为
,代入
,
可得
,,
综上所述,
点坐标为
或
.
②
【解析】
(1)
如图
中,连接
,,,,作
于
,
于
.
由题意可知点
在
上,
,
,
,
,
,,
,
点
是自相似点,
同理可得
,,
,
点
是自相似点.
(2)
②如图
中,满足条件的点
有
个.
以
为圆心
为半径作圆交反比例函数于
,,
以
为圆心
为半径作圆交反比例函数的图象于
,.
【知识点】反比例函数与三角形综合、对应角相等、反比例函数图像上的点的坐标特征、两角分别相等
26.
【答案】
(1)
移项得:合并得:解得:
(2)
方程移项得:合并得:即移项合并得:解得:
【知识点】解常规一元一次方程、移项
合并同类项
27.
【答案】
(1)
(2)
(3)
①点
是点
和点
的中点.
根据题意得:,
解得:.
②点
和点
相遇,
根据题意得:,
解得:.
故
的值为
或
.
【解析】
(1)
的长为
.
(2)
.
【知识点】线段中点的概念及计算、绝对值的几何意义、行程问题
一、选择题(48分)
(2019·期末·江苏苏州市高新区)某服装进货价
元/件,标价为
元/件,商店将此服装打
折销售后仍获利
,则
为
A.
B.
C.
D.
(2019·期末·广东深圳市福田区)如图,正方形
的轨道上有两个点甲与乙,开始时甲在
处,乙在
处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒
,乙的速度为每秒
,已知正方形轨道
的边长为
,则乙在第
次追上甲时的位置在
A.
上
B.
上
C.
上
D.
上
(2019·期末·广东惠州市惠阳区)在解方程
时,去分母后正确的是
A.
B.
C.
D.
(2019·期末·河北石家庄市高邑县)某商店把一件商品按进价增加
作为定价,可是总卖不出去,后来老板把定价降低
,以
元的价格出售,很快就卖出了,则老板卖出这件商品的盈亏情况是
A.亏
元
B.亏
元
C.赚
元
D.不亏不赚
(2019·期中·广东广州市南沙区)若
,
是有理数,下列说法:①若
,则
;②若
,则
;③若
,则
;④若
,则
;⑤若
,则
.其中正确的有
A.
个
B.
个
C.
个
D.
个
(2019·期中·福建厦门市思明区)我国古代数学名著《孙子算经》中记载了一道题,大意是:
匹马拉了
片瓦,已知
匹大马能拉
片瓦,
匹小马能拉
片瓦,问多少匹大马、多少匹小马?若设大马有
匹,那么可列方程为
A.
B.
C.
D.
(2019·期末·陕西西安市雁塔区)在甲处工作的有
人,在乙处工作的有
人,如果要使乙处工作的人数是甲处工作人数的
,应从乙处调多少人到甲处,若设应从乙处调
人到甲处,则下列方程中正确的是
A.
B.
C.
D.
(2020·同步练习)对有理数
,
定义新运算“”:规定
.若
,则
的值为
A.
B.
C.
D.
(2019·期末·天津天津市红桥区)把方程
的分母化为整数后的方程是
A.
B.
C.
D.
(2019·期中·北京北京市朝阳区)
中,
厘米,,
厘米,点
为
的中点.如果点
在线段
上以
厘米/秒的速度由
点向
点运动,同时,点
在线段
上由
点向
点运动.若点
的运动速度为
厘米/秒,则当
与
全等时,
的值为
A.
B.
C.
或
D.
或
(2019·期中·天津天津市红桥区)已知
,,且
,则
的值为
A.
B.
C.
或
D.
或
(2019·期中·山东青岛市市南区)小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位
与注水时间
之间的变化情况的是
A.
B.
C.
D.
(2019·期末·重庆重庆市渝北区)【例
】若
也是图中的格点,且使得
为等腰三角形,则符合条件的点
有
个.
A.
个
B.
个
C.
个
D.
个
(2019·期中·陕西西安市碑林区)在直角坐标系中,
为坐标原点,已知点
,在坐标轴轴上确定点
,使得
为等腰三角形,则符合条件的点
的个数共有
.
A.
个
B.
个
C.
个
D.
个
(2020·专项)邻边不相等的矩形纸片,剪去一个正方形,余下一个四边形,称为第一次操作;在余下的四边形中减去一个正方形,又余下一个四边形,称为第二次操作;以此类推,若第
次操作后余下的四边形是正方形,则称原矩形是
阶矩形.如图,矩形
中,若
,,则矩形
是
阶矩形.已知一个矩形是
阶矩形,较短边长为
,则较长边的长度为
A.
B.
C.
或
D.
或
(2019·期中·吉林长春市朝阳区)已知等腰三角形的两边长
,
满足方程组
则此等腰三角形的周长为
A.
B.
C.
D.
或
二、填空题(18分)
(2018·期末·广东佛山市禅城区)如图,小红将一个正方形纸片剪去一个宽为
的长条后,再从剩下的长方形纸片上剪去一个宽为
的长条,且剪下的两个长条的面积相等.问这个正方形的边长应为多少厘米?设正方形边长为
,则可列方程为
.
(2020·期末·四川绵阳市涪城区)已知:,,,且
到
轴距离为
,则点
的坐标是
.
(2019·期中·北京北京市西城区)若
,则
的值为
.
(2019·期末·呼和浩特市)一元一次方程
的解是
.
(2018·期中·辽宁大连市西岗区)在平面直角坐标系中,已知点
,,以原点
为位似中心,相似比为
,把
缩小为
,则点
的对应点
的坐标是
.
(2020·期末·四川绵阳市涪城区)已知正整数
,,
满足
,,则
.
(2018·期末·甘肃兰州市城关区)如图,长方体的长为
,宽为
,高为
,点
离点
的距离为
,一只蚂蚁如果要沿着长方体的表面从点
爬到点
,需要爬行的最短距离是
.
三、解答题(56分)
(2019·期末·山东济南市历城区)如图,直线
与
轴、
轴分别交于点
和点
,
是
的上的一点,若将
沿
折叠,点
恰好落在
轴上的点
处.
(1)
求
,
两点的坐标;
(2)
求直线
的表达式;
(3)
在
轴上是否存在点
,使得以点
,,
为顶点的三角形是等腰三角形,若存在,请直接写出所有点
的坐标;若不存在,请说明理由.
(2019·期中·北京北京市东城区)定义:点
为
内部或边上的点,若满足
,,
至少有一个三角形与
相似(点
不与
顶点重合),则称点
为
的自相似点.
例如:如图
,点
在
的内部,,,则
,故点
为
的自相似点.在平面直角坐标系
中.
(1)
点
坐标为
,
轴于
点,在
,,
这三个点中,其中是
自相似点的是
(填字母);
(2)
若点
是曲线
上的一个动点,
为
轴正半轴上一个动点;
①如图
,,
点横坐标为
,且
,若点
是
的自相似点,求点
的坐标;
②若
,点
为
,且
的自相似点有
个,则曲线
上满足这样条件的点
共有
个,请在图
中画出这些点(保留必要的画图痕迹).
(2019·期末·江苏苏州市姑苏区)解下列方程:
(1)
;
(2)
.
(2018·期末·云南昆明市官渡区)已知数轴上三点
,,
对应的数分别为
,,,点
为数轴上任意点,其对应的数为
.
(1)
的长为
.
(2)
如果点
到点
,点
的距离相等,那么
的值是:
.
(3)
如果点
以每分钟
个单位长度的速度从点
向左运动,同时点
和点
分别以每分钟
个单位长度和每分钟
个单位长度的速度也向左运动,设
分钟时点
到点
,点
的距离相等,求
的值.
答案
一、选择题
1.
【答案】B
【解析】根据题意得:,
解得:.
【知识点】利润问题
2.
【答案】D
【解析】设乙走
秒第一次追上甲.
根据题意,得
,
解得
.
乙走
秒第一次追上甲,则乙在第
次追上甲时的位置是
上;
设乙再走
秒第二次追上甲.
根据题意,得
,解得
.
乙再走
秒第二次追上甲,则乙在第
次追上甲时的位置是
上;
同理:
乙再走
秒第三次次追上甲,则乙在第
次追上甲时的位置是
上;
乙再走
秒第四次追上甲,则乙在第
次追上甲时的位置是
上;
乙在第
次追上甲时的位置又回到
上;
,
乙在第
次追上甲时的位置是
上.
【知识点】行程问题、用代数式表示规律
3.
【答案】D
【解析】去分母得:.
【知识点】去分母
去括号
4.
【答案】A
【解析】设商品进价为
,根据题意得:
解得
,
以
元出售,可见亏
元.
【知识点】利润问题
5.
【答案】B
【解析】①若
,则
不一定小于
,如
,,故①错误;
②若
,则
不一定大于
,如
,,故②错误;
③若
,则
,故③正确;
④若
,则
可能等于
,如
,,,故④错误;
⑤若
,则
,故⑤正确,
正确的有③和⑤,一共
个.
故选B.
【知识点】利用绝对值比较数的大小
6.
【答案】D
【解析】设大马有
匹,则小马有
匹,
由题意,得
.
【知识点】和差倍分
7.
【答案】D
【解析】设应从乙处调
人到甲处,
则甲处现有的工作人数为
人,
乙处现有的工作人数为
人.
根据“乙处工作的人数是甲处工作人数的
,”
列方程得:.
【知识点】和差倍分
8.
【答案】D
【知识点】去分母
去括号
9.
【答案】D
【知识点】去分母
去括号
10.
【答案】C
【知识点】边角边
11.
【答案】D
【解析】
,
,
,
,
又
,由于
,,而
,,
则
只能取
,
取
或
,
或
.
则
的值为
或
.
【知识点】绝对值的性质
12.
【答案】B
【解析】一注水管向小玻璃杯内注水,水面在逐渐升高,当小杯中水满时,开始向大桶内流,这时水位高度不变.当桶内水面高度与小杯一样后,再继续注水,水面高度在升高,升高的比开始变慢.
【知识点】用函数图象表示实际问题中的函数关系
13.
【答案】C
【解析】如图:
分情况讨论.
①
为等腰
底边时,符合条件的
点有
个;
②
为等腰
其中的一条腰时,符合条件的
点有
个.
故选:C.
【知识点】垂直平分线的性质、等腰三角形的概念
14.
【答案】D
【解析】根据已知线段构造等腰三角形.
①以
为圆心,以
为半径作圆,交于坐标轴两点;
②以
为圆心,以
为半径作圆,此时交坐标轴四个点;
③作线段
垂直平分线,交坐标轴两个点,共
个点.
【知识点】等腰三角形的概念
15.
【答案】D
【知识点】矩形的性质、正方形的性质
16.
【答案】A
【解析】
解不等式组可得
等腰三角形的两边长为
,,
三边可能情况为
,,
或
,,,
,,
不能构成三角形,
等腰三角形的周长为
.
【知识点】等腰三角形的概念
二、填空题
17.
【答案】
;
【解析】设正方形边长为
,
由题意得:,
故答案为:.
【知识点】几何问题
18.
【答案】
或
;
【解析】因为
,
所以
,
因为点
到
轴距离为
,
所以
,
所以点
的坐标为
或
.
【知识点】连线与坐标轴平行的两点间距离
19.
【答案】
或
;
【解析】
,
,
.
【知识点】含绝对值的一元一次方程的解法
20.
【答案】
;
【解析】去分母得:,
移项得:,
合并同类项得:,
系数化为
得:.
故答案为:.
【知识点】去分母
去括号
21.
【答案】
或
;
【解析】
点
,以原点
为位似中心,相似比为
,把
缩小,
对应点都乘以
或
,
则点
的对应点坐标为
或
.
【知识点】位似图形的性质应用
22.
【答案】
;
【解析】由题
由②知:,
,,
均为正整数,即
,,
且为整数,
为偶数且
,,
①
,,代入①,②,
即
故
,,,
此时
;
②
时,
代入①,②,
即
不满足;
③
时,,
即
此时解出
不满足,
继续变大时,解出的
更小,
故仅
,,
满足,
.
故答案为:.
【知识点】代入消元法转为二元一次方程(组)
23.
【答案】
;
【解析】三种情况:
由于
,故最短距离为
.
【知识点】平面展开-最短路径问题
三、解答题
24.
【答案】
(1)
当
时,,
,
当
时,,,
.
(2)
在
中,,,,
,
由折叠得:,
,
设
,则
,
由勾股定理得:,,
,
设
,
则
解得:
直线
的解析式为:.
(3)
点的坐标为
或
或
或
.
【解析】
(3)
在
轴上存在点
,使得以点
,,
为顶点的三角形是等腰二角形,如图.
,,
,
当
时,,;
当
时,,
当
时,作
的垂直平分线,交
轴于
,交
与
,连接
,
设
,则
,
,
,解得
,
.
综上,
点的坐标为
或
或
或
.
【知识点】一次函数的解析式、一次函数与三角形的综合、等腰三角形的判定
25.
【答案】
(1)
(2)
①如图
,过点
作
轴于
点.
点的横坐标为
,
,
,
,,,
直线
的表达式为
,
在
中,,,
设
,则
,
,
,
,,
,,
,
是等边三角形,
,
的横坐标为
,
的横坐标为
,代入
,
可得
,,
综上所述,
点坐标为
或
.
②
【解析】
(1)
如图
中,连接
,,,,作
于
,
于
.
由题意可知点
在
上,
,
,
,
,
,,
,
点
是自相似点,
同理可得
,,
,
点
是自相似点.
(2)
②如图
中,满足条件的点
有
个.
以
为圆心
为半径作圆交反比例函数于
,,
以
为圆心
为半径作圆交反比例函数的图象于
,.
【知识点】反比例函数与三角形综合、对应角相等、反比例函数图像上的点的坐标特征、两角分别相等
26.
【答案】
(1)
移项得:合并得:解得:
(2)
方程移项得:合并得:即移项合并得:解得:
【知识点】解常规一元一次方程、移项
合并同类项
27.
【答案】
(1)
(2)
(3)
①点
是点
和点
的中点.
根据题意得:,
解得:.
②点
和点
相遇,
根据题意得:,
解得:.
故
的值为
或
.
【解析】
(1)
的长为
.
(2)
.
【知识点】线段中点的概念及计算、绝对值的几何意义、行程问题
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
