北师大版八年级上册数学八年级上册 1.1 勾股定理(1)(共22张PPT)
文档属性
| 名称 | 北师大版八年级上册数学八年级上册 1.1 勾股定理(1)(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 15:12:58 | ||
图片预览


文档简介
(共22张PPT)
第一章
勾股定理
1
探索勾股定理
(第1课时)
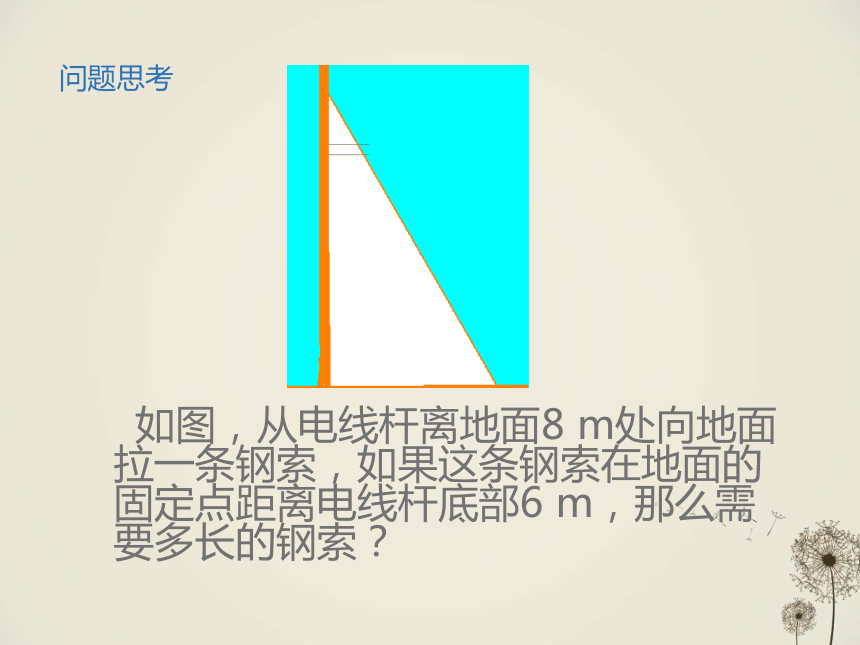
问题思考
如图,从电线杆离地面8
m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6
m,那么需要多长的钢索?
A
B
C
A
B
C
图1-1
图1-2
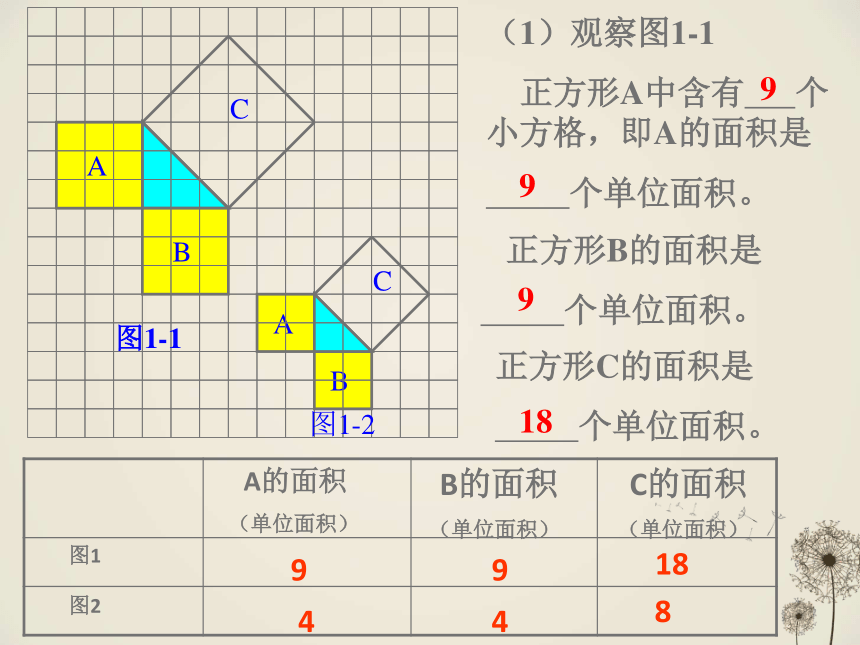
(1)观察图1-1
正方形A中含有
个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
18
A的面积
(单位面积)
B的面积
(单位面积)
C的面积
(单位面积)
图1
图2
9
9
18
4
4
8
A
B
C
A
B
C
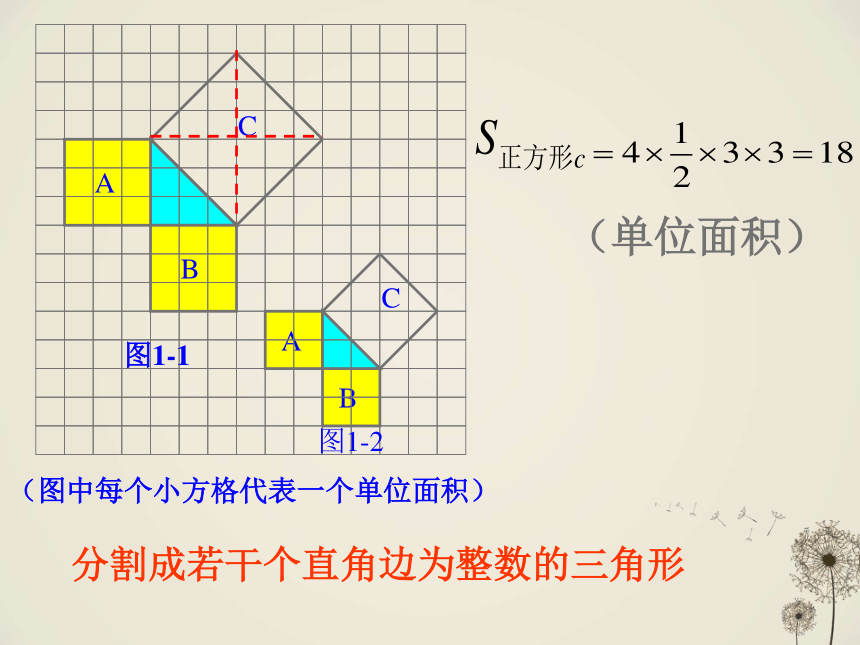
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(单位面积)
分割成若干个直角边为整数的三角形
A
B
C
A
B
C
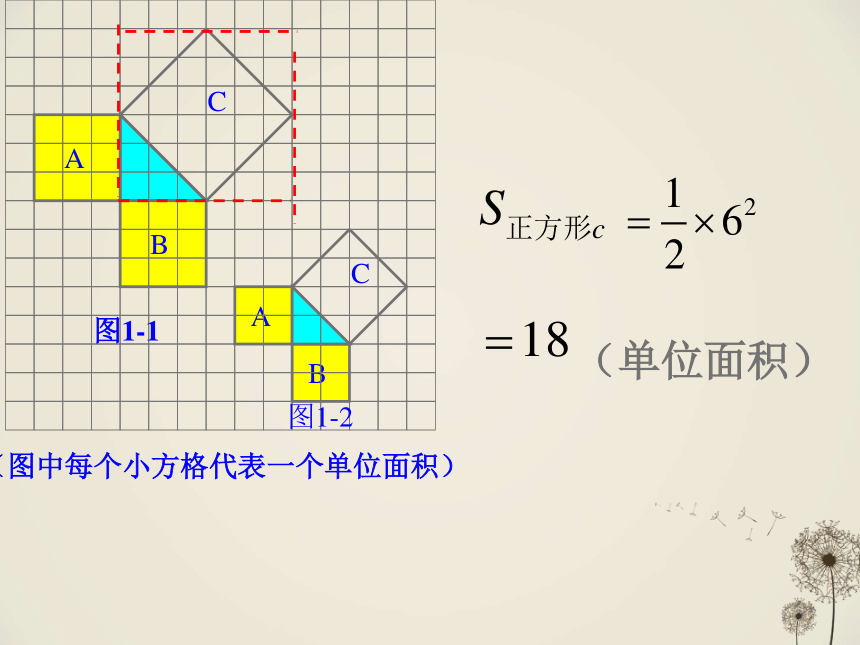
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(单位面积)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
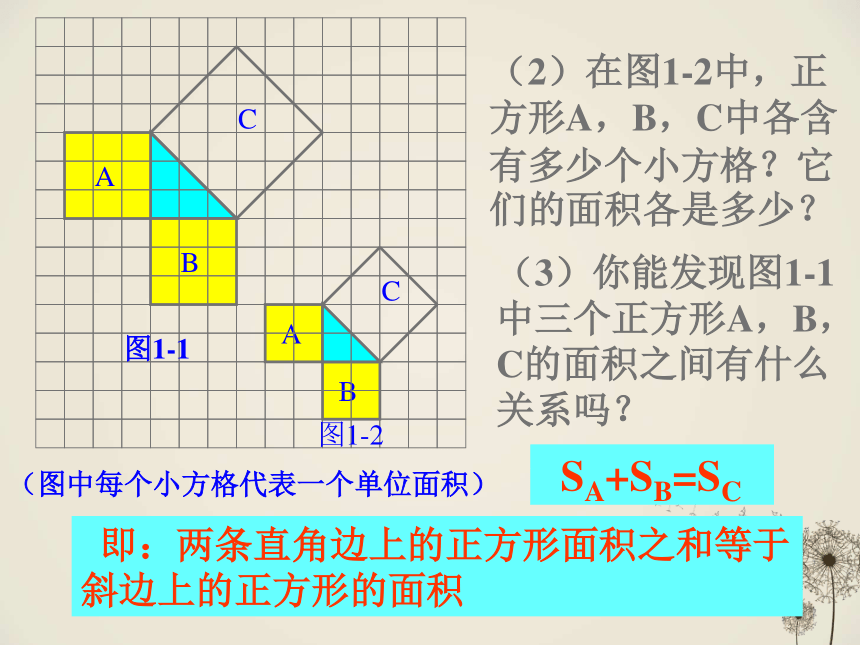
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于
斜边上的正方形的面积
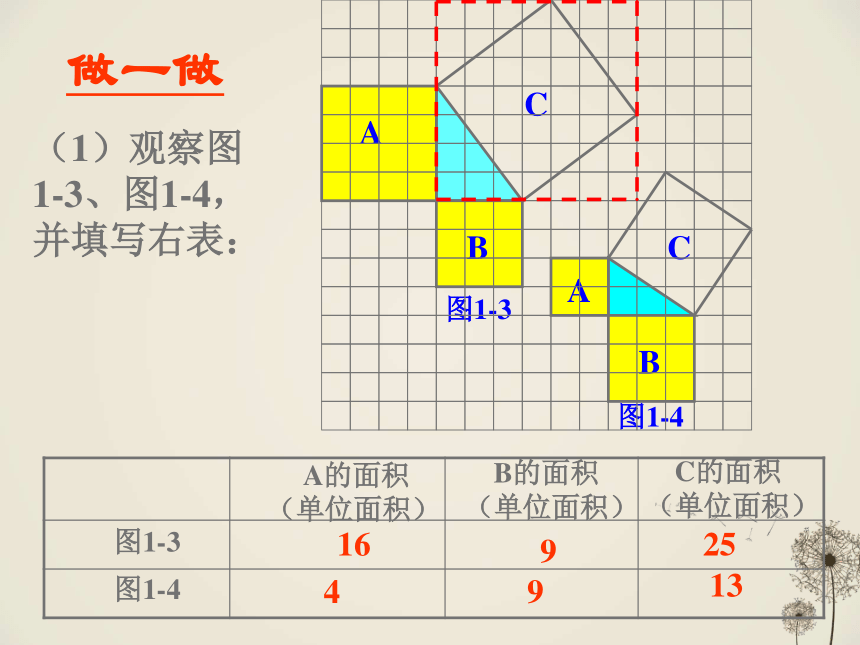
做一做
(1)观察图1-3、图1-4,并填写右表:
A
B
C
图1-3
A
B
C
图1-4
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1-3
图1-4
16
9
25
4
9
13
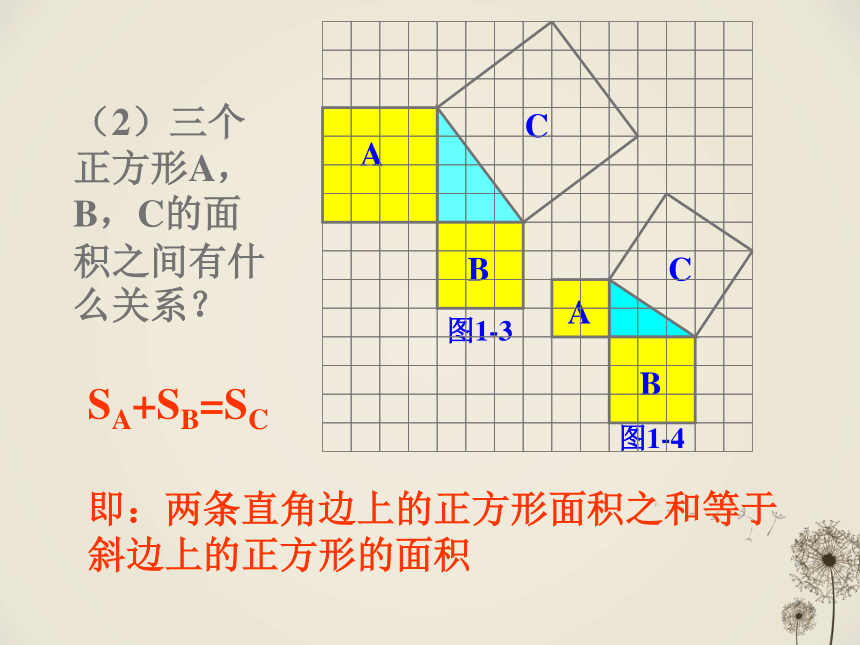
(2)三个正方形A,B,C的面积之间有什么关系?
A
B
C
图1-3
A
B
C
图1-4
SA+SB=SC
即:两条直角边上的正方形面积之和等于
斜边上的正方形的面积
(3)如果直角三角形的两直角边分别为1.6个单位长度和2.4个单位长度,上面所猜想的数量关系还成立吗?说明你的理由。
A
B
C
a
c
b
SA+SB=SC
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c
之间的关系?
a2+b2=c2
勾股定理(gou-gu
theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
即
直角三角形两直角边的平方和等于斜边的平方。
勾
股
弦
在西方又称毕达哥拉斯定理耶!
课堂
练
习
求出下列直角三角形中未知边的长度。
3
x
17
8
4
X
生活情景
如图所示,一棵大树在一次强烈台风中于离地面9米处折断倒下,树梢落在离树根12米处.大树在折断之前高多少?
想一想
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度
∵
荧屏对角线大约为74厘米
∴售货员没搞错
检测反馈
1.直角三角形ABC的两直角边BC=12,AC=16,则△ABC的斜边AB的长是
( )
A.20 B.10 C.9.6 D.8
A
2.直角三角形两直角边长分别是6和8,则周长与最短边长的比是
( )
A.7∶1
B.4∶1
C.25∶7
D.31∶7
B
3.(2015·温州模拟)如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,若BC=10,AD=12,则AC= .?
13
4.
如图所示,在Rt△ABC中,∠ACB=90°,AB=10,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于 .?
12.5π
小结
1.这一节课我们一起学习了哪些知识和思想方法?
2.对这些内容你有什么体会?请与你的同伴交流.
作业
一、
习题1.1
第1题
习题1.1
第1、4题
二、准备4张全等的直角三角形纸片
a
b
c
如图所示,强大的台风使得一根旗杆在离地面9米处折断倒下,旗杆顶落在离旗杆底部12米处.
旗杆折断之前有多高?
A
B
C
第一章
勾股定理
1
探索勾股定理
(第1课时)
问题思考
如图,从电线杆离地面8
m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6
m,那么需要多长的钢索?
A
B
C
A
B
C
图1-1
图1-2
(1)观察图1-1
正方形A中含有
个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
18
A的面积
(单位面积)
B的面积
(单位面积)
C的面积
(单位面积)
图1
图2
9
9
18
4
4
8
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(单位面积)
分割成若干个直角边为整数的三角形
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(单位面积)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于
斜边上的正方形的面积
做一做
(1)观察图1-3、图1-4,并填写右表:
A
B
C
图1-3
A
B
C
图1-4
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1-3
图1-4
16
9
25
4
9
13
(2)三个正方形A,B,C的面积之间有什么关系?
A
B
C
图1-3
A
B
C
图1-4
SA+SB=SC
即:两条直角边上的正方形面积之和等于
斜边上的正方形的面积
(3)如果直角三角形的两直角边分别为1.6个单位长度和2.4个单位长度,上面所猜想的数量关系还成立吗?说明你的理由。
A
B
C
a
c
b
SA+SB=SC
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c
之间的关系?
a2+b2=c2
勾股定理(gou-gu
theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
即
直角三角形两直角边的平方和等于斜边的平方。
勾
股
弦
在西方又称毕达哥拉斯定理耶!
课堂
练
习
求出下列直角三角形中未知边的长度。
3
x
17
8
4
X
生活情景
如图所示,一棵大树在一次强烈台风中于离地面9米处折断倒下,树梢落在离树根12米处.大树在折断之前高多少?
想一想
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度
∵
荧屏对角线大约为74厘米
∴售货员没搞错
检测反馈
1.直角三角形ABC的两直角边BC=12,AC=16,则△ABC的斜边AB的长是
( )
A.20 B.10 C.9.6 D.8
A
2.直角三角形两直角边长分别是6和8,则周长与最短边长的比是
( )
A.7∶1
B.4∶1
C.25∶7
D.31∶7
B
3.(2015·温州模拟)如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,若BC=10,AD=12,则AC= .?
13
4.
如图所示,在Rt△ABC中,∠ACB=90°,AB=10,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于 .?
12.5π
小结
1.这一节课我们一起学习了哪些知识和思想方法?
2.对这些内容你有什么体会?请与你的同伴交流.
作业
一、
习题1.1
第1题
习题1.1
第1、4题
二、准备4张全等的直角三角形纸片
a
b
c
如图所示,强大的台风使得一根旗杆在离地面9米处折断倒下,旗杆顶落在离旗杆底部12米处.
旗杆折断之前有多高?
A
B
C
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
