27.4 正多边形和圆(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
华东师大版27.4 正多边形和圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线上的一点.若∠CBE=40°,则∠AOC等于( )
A.20° B.40° C.80° D.100°
2.圆的内接四边形ABCD的四个内角之比∠A:∠B:∠C:∠D的可能的值是( ).
A.1:2:3:4 B.4:2:3:1 C.4:3:1:2 D.4:1:3:2
3.如图,四边形ABCD是⊙O的内接四边形,若∠B=80°,则∠ADC的度数是( )
A.60° B.80° C.90° D.100°
4.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
5.若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6等于( )
A. B. C. D.
6.正五边形的中心角等于( )
A.18° B.36° C.54° D.72°
7.正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据应( )
A.把圆等分,顺次连接各分点得到的多边形是圆的内接正边形
B.把圆等分,依次过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正边形
C.各边相等,并且各角也相等的多边形是正多边形
D.用量角器等分圆是一种简单而常用的方法
二、填空题
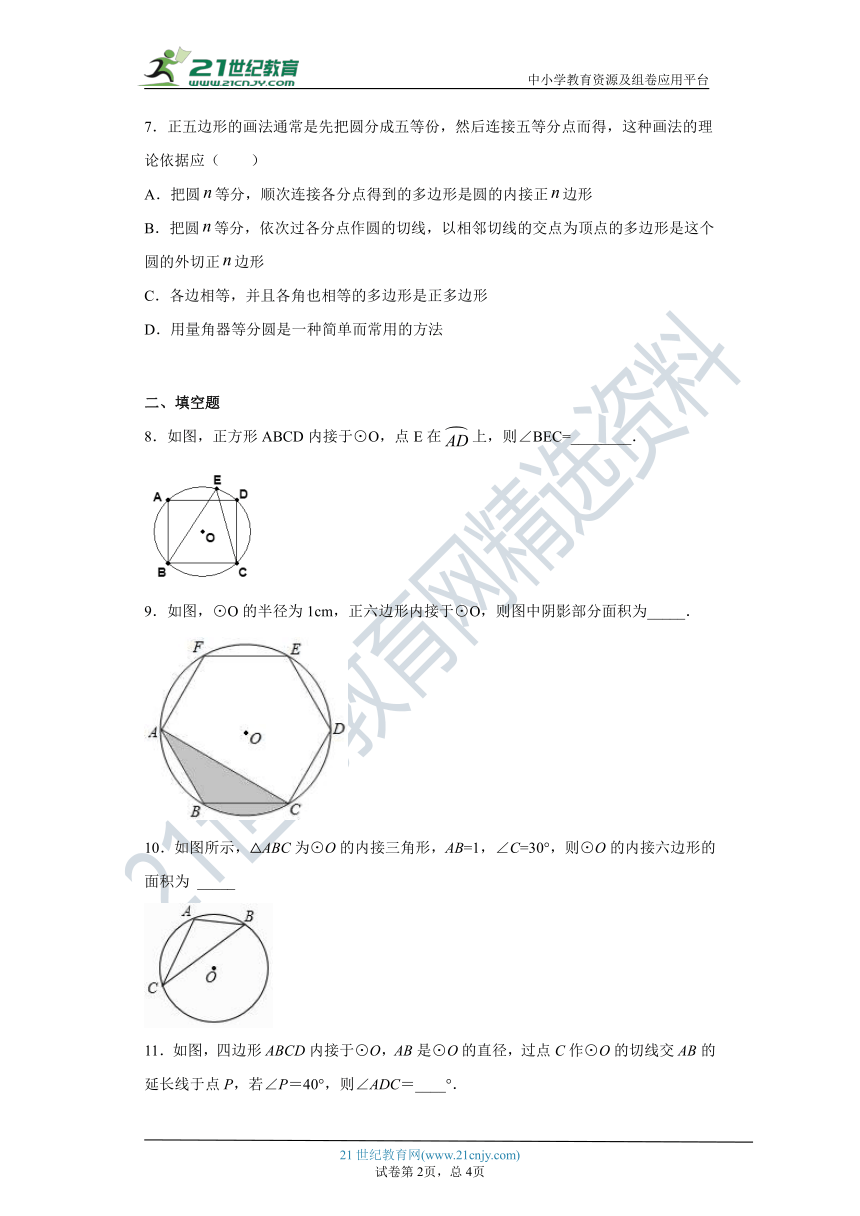
8.如图,正方形ABCD内接于⊙O,点E在上,则∠BEC=________.
9.如图,⊙O的半径为1cm,正六边形内接于⊙O,则图中阴影部分面积为_____.
10.如图所示,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接六边形的面积为 _____
11.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,若∠P=40°,则∠ADC=____°.
三、解答题
12.在圆内接四边形中,,,的度数比是,求四边各内角的度数.
13.如图所示,四边形ABCD内接于⊙O,延长AD,BC相交于点M,延长AB,DC相交于点N,∠M=40°,∠N=20°,求∠A的度数.
14.如图,⊙O与四边形ABCD的各边依次切于M,N,G,H.
(1)猜想AB+CD与AD+BC有何数量关系,并证明你的猜想;
(2)若四边形ABCD增加条件AD∥BC而成为梯形,梯形的中位线长为m,其他条件不变,试用m表示梯形的周长.
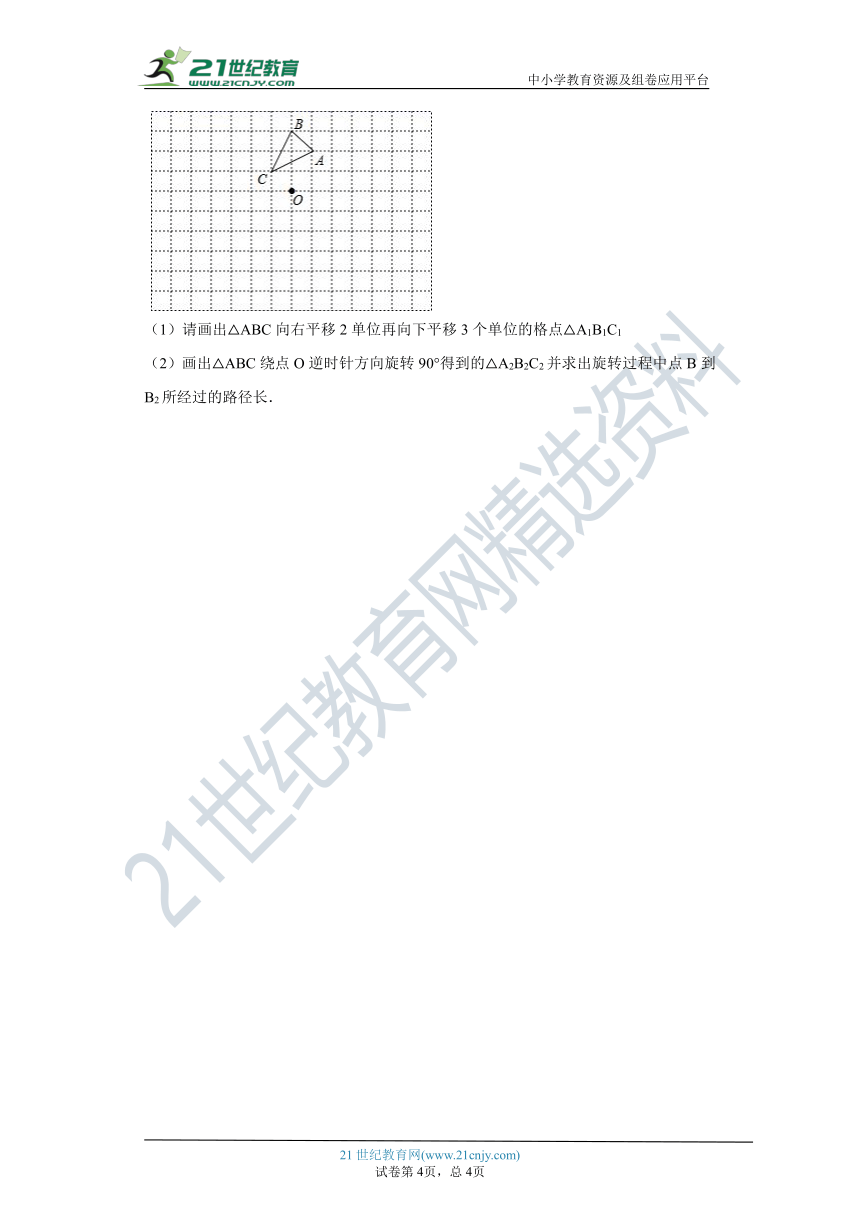
15.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的位置如图所示(顶点是网格线的交点)
(1)请画出△ABC向右平移2单位再向下平移3个单位的格点△A1B1C1
(2)画出△ABC绕点O逆时针方向旋转90°得到的△A2B2C2并求出旋转过程中点B到B2所经过的路径长.
参考答案
1.C
解析:
因为四边形ABCD为⊙O的内接四边形,∠CBE=40°,所以∠D=40°,所以∠AOC=80°.
2.C
解析:
∵四边形ABCD是圆内接四边形,
∴∠A+∠C=∠B+∠D=180°.
∴圆内接四边形ABCD的四个内角之比可能是:4:3:1:2.
故选C.
3.D
解析:
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC=180°-∠B=180°-80°=100°.
故选D.
4.B
解析:
解:内心到三角形三边距离相等,到角的两边距离相等的点在这个角的角平分线上,
故选:B.
5.A
解析:
解:设圆的半径为R,
则正三角形的边心距为R×cos60°.
四边形的边心距为R×cos45°,
正六边形的边心距为R×cos30°.
∴等于 .
故选A.
6.D
解析:
解:正五边形的中心角为.
故选D
7.A
解析:
正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据是把圆等分,顺次连接各分点得到的多边形是圆的内接正边形.
故选A.
8..
解析:
解:连接OB、OC,则∠E=∠BOC,
∵O是正方形外接圆的圆心,
∴∠BOC=90°,
∴∠BEC=∠BOC=45°.
9.
解析:
解:如图,连接BO,CO,OA.
由题意得,△OBC,△AOB都是等边三角形,
∴∠AOB=∠OBC=60°,
∴OA∥BC,
∴△OBC的面积=△ABC的面积,
∴图中阴影部分的面积等于扇形OBC的面积=.
故答案为
10.
解析:
试题解析:连接AO,BO,过点O作OE⊥AB于点E,
∵∠C=30°,
∴∠AOB=60°,
∵AO=BO,
∴△AOB是等边三角形,
∴AO=BO=AB=1,
∴EO=sin60°×1=,
,
∴⊙O的内接六边形的面积为:6×=.
故答案为:.
11.115°
解析:
解:连接OC,如右图所示,
由题意可得,∠OCP=90°,∠P=40°,
∴∠COB=50°,
∵OC=OB,
∴∠OCB=∠OBC=65°,
∵四边形ABCD是圆内接四边形,
∴∠D+∠ABC=180°,
∴∠D=115°,
故答案为:115°.
12.四边形各内角的度数分别是,,,.
解析:
依题意,设,,,
∴,∴.
∴,,.
∴.
∴四边形各内角的度数分别是,,,.
13.∠A=60°.
解析:
∵四边形ABCD内接于⊙O
∴∠1=∠2=∠A.
∵∠ADC+∠ABC=180°,∠ADC=∠M+∠2,∠ABC=∠1+∠N,
∴∠M+∠1+∠2+∠N=180°
∵∠M=40°,∠N=20°,∠1=∠2=∠A
∴∠A=60°.
14.(1)AB+CD=AD+BC,证明详见解析;(2)4m.
解析:
(1)AB+CD=AD+BC
证明:由切线长定理,得:AM=AH,BN=BM,CN=CG,DG=DH,
所以AB+CD=AM+BM+CG+DG=AH+BN+CN+DH=AD+BC,
即AB+CD=AD+BC
(2)AD∥BC,在梯形ABCD中,由梯形的中位线定理得,
AD+BC=2m,
梯形的周长=AB+CD+AD+BC=2(AD+BC)=2×2m=4m
15.(1)如图所示;见解析;(2)=π.
解析:
(1)如图;
(2)如图;
旋转过程中,点B到B2所经过的路径长为以OB为半径,90°为圆心角的弧长,2π×3π.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
华东师大版27.4 正多边形和圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线上的一点.若∠CBE=40°,则∠AOC等于( )
A.20° B.40° C.80° D.100°
2.圆的内接四边形ABCD的四个内角之比∠A:∠B:∠C:∠D的可能的值是( ).
A.1:2:3:4 B.4:2:3:1 C.4:3:1:2 D.4:1:3:2
3.如图,四边形ABCD是⊙O的内接四边形,若∠B=80°,则∠ADC的度数是( )
A.60° B.80° C.90° D.100°
4.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
5.若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6等于( )
A. B. C. D.
6.正五边形的中心角等于( )
A.18° B.36° C.54° D.72°
7.正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据应( )
A.把圆等分,顺次连接各分点得到的多边形是圆的内接正边形
B.把圆等分,依次过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正边形
C.各边相等,并且各角也相等的多边形是正多边形
D.用量角器等分圆是一种简单而常用的方法
二、填空题
8.如图,正方形ABCD内接于⊙O,点E在上,则∠BEC=________.
9.如图,⊙O的半径为1cm,正六边形内接于⊙O,则图中阴影部分面积为_____.
10.如图所示,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接六边形的面积为 _____
11.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,若∠P=40°,则∠ADC=____°.
三、解答题
12.在圆内接四边形中,,,的度数比是,求四边各内角的度数.
13.如图所示,四边形ABCD内接于⊙O,延长AD,BC相交于点M,延长AB,DC相交于点N,∠M=40°,∠N=20°,求∠A的度数.
14.如图,⊙O与四边形ABCD的各边依次切于M,N,G,H.
(1)猜想AB+CD与AD+BC有何数量关系,并证明你的猜想;
(2)若四边形ABCD增加条件AD∥BC而成为梯形,梯形的中位线长为m,其他条件不变,试用m表示梯形的周长.
15.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的位置如图所示(顶点是网格线的交点)
(1)请画出△ABC向右平移2单位再向下平移3个单位的格点△A1B1C1
(2)画出△ABC绕点O逆时针方向旋转90°得到的△A2B2C2并求出旋转过程中点B到B2所经过的路径长.
参考答案
1.C
解析:
因为四边形ABCD为⊙O的内接四边形,∠CBE=40°,所以∠D=40°,所以∠AOC=80°.
2.C
解析:
∵四边形ABCD是圆内接四边形,
∴∠A+∠C=∠B+∠D=180°.
∴圆内接四边形ABCD的四个内角之比可能是:4:3:1:2.
故选C.
3.D
解析:
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC=180°-∠B=180°-80°=100°.
故选D.
4.B
解析:
解:内心到三角形三边距离相等,到角的两边距离相等的点在这个角的角平分线上,
故选:B.
5.A
解析:
解:设圆的半径为R,
则正三角形的边心距为R×cos60°.
四边形的边心距为R×cos45°,
正六边形的边心距为R×cos30°.
∴等于 .
故选A.
6.D
解析:
解:正五边形的中心角为.
故选D
7.A
解析:
正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据是把圆等分,顺次连接各分点得到的多边形是圆的内接正边形.
故选A.
8..
解析:
解:连接OB、OC,则∠E=∠BOC,
∵O是正方形外接圆的圆心,
∴∠BOC=90°,
∴∠BEC=∠BOC=45°.
9.
解析:
解:如图,连接BO,CO,OA.
由题意得,△OBC,△AOB都是等边三角形,
∴∠AOB=∠OBC=60°,
∴OA∥BC,
∴△OBC的面积=△ABC的面积,
∴图中阴影部分的面积等于扇形OBC的面积=.
故答案为
10.
解析:
试题解析:连接AO,BO,过点O作OE⊥AB于点E,
∵∠C=30°,
∴∠AOB=60°,
∵AO=BO,
∴△AOB是等边三角形,
∴AO=BO=AB=1,
∴EO=sin60°×1=,
,
∴⊙O的内接六边形的面积为:6×=.
故答案为:.
11.115°
解析:
解:连接OC,如右图所示,
由题意可得,∠OCP=90°,∠P=40°,
∴∠COB=50°,
∵OC=OB,
∴∠OCB=∠OBC=65°,
∵四边形ABCD是圆内接四边形,
∴∠D+∠ABC=180°,
∴∠D=115°,
故答案为:115°.
12.四边形各内角的度数分别是,,,.
解析:
依题意,设,,,
∴,∴.
∴,,.
∴.
∴四边形各内角的度数分别是,,,.
13.∠A=60°.
解析:
∵四边形ABCD内接于⊙O
∴∠1=∠2=∠A.
∵∠ADC+∠ABC=180°,∠ADC=∠M+∠2,∠ABC=∠1+∠N,
∴∠M+∠1+∠2+∠N=180°
∵∠M=40°,∠N=20°,∠1=∠2=∠A
∴∠A=60°.
14.(1)AB+CD=AD+BC,证明详见解析;(2)4m.
解析:
(1)AB+CD=AD+BC
证明:由切线长定理,得:AM=AH,BN=BM,CN=CG,DG=DH,
所以AB+CD=AM+BM+CG+DG=AH+BN+CN+DH=AD+BC,
即AB+CD=AD+BC
(2)AD∥BC,在梯形ABCD中,由梯形的中位线定理得,
AD+BC=2m,
梯形的周长=AB+CD+AD+BC=2(AD+BC)=2×2m=4m
15.(1)如图所示;见解析;(2)=π.
解析:
(1)如图;
(2)如图;
旋转过程中,点B到B2所经过的路径长为以OB为半径,90°为圆心角的弧长,2π×3π.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
