湘教版七年级数学上册第4章复习知识要点+复习题(共30张ppt)
文档属性
| 名称 | 湘教版七年级数学上册第4章复习知识要点+复习题(共30张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 637.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
1.
了解几何图形的分类,初步认识一些简单的图形。
2.
理解线段、射线、直线的关系,并能用恰当的方法表
示它们。掌握直线的基本事实。
3.
会比较线段的长度,用尺规作两条直线的和或差。能解决
与线段的中点有关。
4.
掌握角的有关概念及计算,余角和补角的性质及其应用;
4.
培养学生看图识图用图能力,体验数形结合思想.
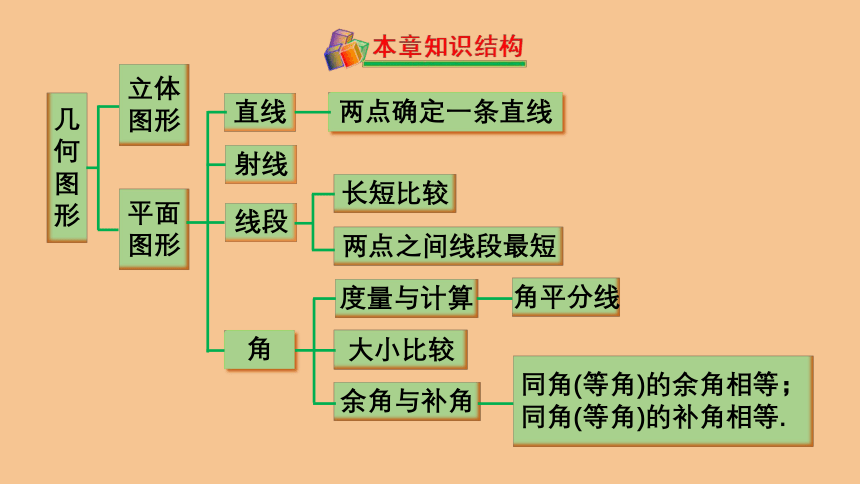
几
何
图
形
立体
图形
平面
图形
直线
射线
线段
角
两点确定一条直线
长短比较
两点之间线段最短
度量与计算
大小比较
余角与补角
角平分线
同角(等角)的余角相等;
同角(等角)的补角相等.
1、几何图形包括立体图形和平面图形。我们学过的立体图
形有圆柱、
,圆锥、
和球。
要点复习
2、线段有2个端点,射线有1个端点,直线没有端点。将线
段向一个方向延长形成
,向两个相反的方向延
长形成
.
棱柱
棱锥
3、过
有且只有一条直线。即
确定一条直线。
射线
直线
两点
线段
4、两点之间的所有连线中,
最短.
两点
6、比较两个角的大小的方法有
和
。
7、如图,点B是AC的中点,线段AB、BC、AC的大小关
系是
。
5、比较线段长短的方法有
和
.
度量法
截取法
度量法
叠合法
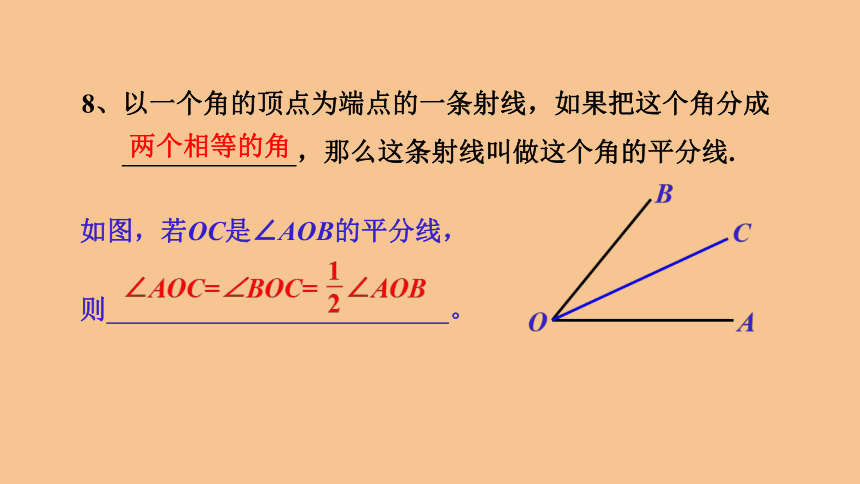
8、以一个角的顶点为端点的一条射线,如果把这个角分成
,那么这条射线叫做这个角的平分线.
如图,若OC是∠AOB的平分线,
则
。
两个相等的角
9、角的大小由角的始边绕顶点旋转到终边时的
的大
小决定,而与所画角的两边的长度
.
无关
旋转量
10、度量角的基本单位有度、分、秒。角度单位之间的进率
是
,即
60
60
60
11、如果两个角的和等于一个
,那么这两个角互为余角.
直角
12、如果两个角的和等于一个
,那么这两个角互为补角.
平角
13、同角或等角的余角
,同角或等角的补角
.
相等
相等
14、如果a=b,c=b,那么
.
这叫
.
a=c
等量代换
要点突破
(一)图形的认识
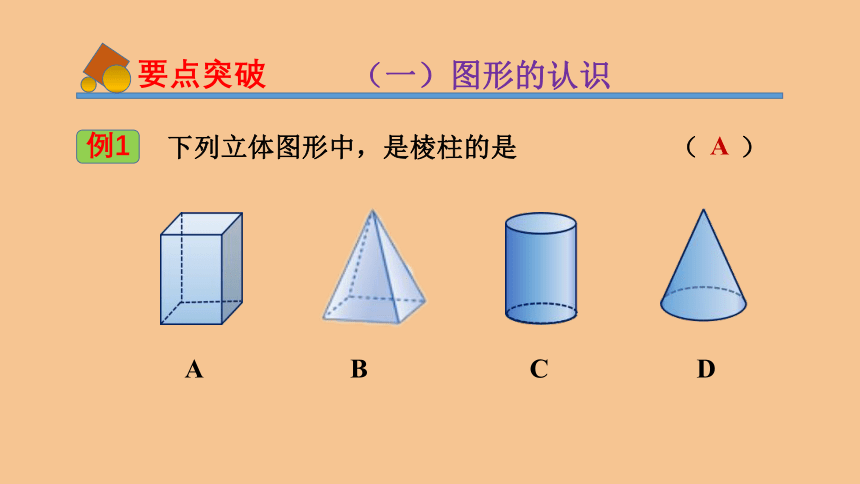
例1
下列立体图形中,是棱柱的是
(
)
A
B
C
D
A
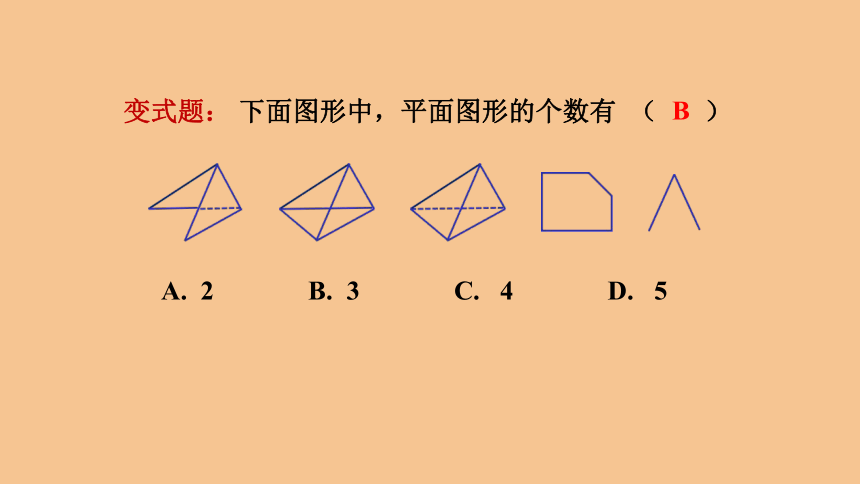
变式题:
下面图形中,平面图形的个数有
(
)
A.
2
B.
3
C.
4
D.
5
B
要点突破
(二)线段、射线、直线的性质
例2
随着我国路桥修建技术的提高,现在我国设计的高速公路桥梁多、隧道多,从而缩短了路程。其依据是(
)
A.
两点确定一条直线
B.
直线比曲线短
C.
两点之间,线段最短
D.
两条直线相交于一点
经过两点,确定一条直线
变式题1:砖匠师傅砌墙时,先将两端固定拉线,再沿着线砌墙,其原理是
.
C
变式题2:
下列说法正确的有
(
)
①射线的长度是直线长度的一半
②将射线AO反向无限延长得到直线OA
③右图中的线段共有3条
④在体育课排队时,体育老师在每一列取两个点,则经过
这两点可以画出唯一的一条直线
A.
①②
B.
②③
C.①③
D.
②④
D
要点突破
(三)线段的有关计算
例3
解:因为点D是AC的中点,AD=2.5cm,所以AC=2DC=5cm,DC=AD=2.5cm,从而BC=2DC=5cm.
所以,AB=2AC=10cm.
如图,已知点D是AC的中点,BC=2DC,AD=2.5cm,
求线段AB的长.
变式题:如图,已知
,E,F分别是AB,BC的中点,EF=7,求线段AB,DC的长.
A
D
C
B
E
F
A
D
C
B
E
F
提示:由
可得AB=3BD,BC=4BD,由E,F分别是AB,BC的中点,可得
求出BD=2,即可求出AB,DC的长。
要点突破
(四)角的有关计算
例4
解:因为∠DOC是∠D的余角,且∠D=60°,所以∠DOC=90°-60°=30°,又∠BOC=15°,所以,∠α=∠DOC-
∠BOC=30°-15°=15°.
因为∠AOD是∠α的余角,所以,
∠AOD=90°-15°=75°.
如图,将一副三角尺按如图位置放置,∠D=60°,量得∠BOC=15°,求∠α,∠AOD的度数.
变式题:
如图,点O是直线AB上的一点,OD平分∠AOC,OE
平分∠BOC,求∠DOE的度数.
A
O
D
B
C
E
要点突破
(五)简单作图题
例5
如图,已知线段AB=6,按以下要求完成作图并计算.
(1)延长线段AB,使BC=2AB(用圆规截取,保留作图痕迹);
(2)取线段AC的中点D,求出线段DB的长。
A
B
A
B
C
D
解:(1)如图所示:
(2)
BC=2AB=2×6=12,AC=AB+BC=6+12=18.
因为点D是AC的中点,所以AD=9,BD=AD-AB=3.
1.
图(a)中线段和射线的条数分别是
(
)
A.
2,2
B.
2,4
C.
3,4
D.
3,6
A
B
C
2.
图(b)小于平角的角共有
个,其中可用一个大写字母表示的角是
.
A
D
B
C
(a)
(b)
D
7
●基础巩固题
∠B,∠C
3.
如图,线段AB=6cm,点C是AB的中点,点D是AC的中点,
则线段DC的长为
cm.
4.
如图,线段AB=10cm,AD=2.5cm,点D是线段AC的中点,则线段BC的长为
cm.
1.5
5
5.
(易错题)已知线段AB=8cm,直线上有一点C,且BC=4cm,点P线段是AC的中点,则AP的长为
(
)
A.
2cm
B.
4cm
C.
2cm或6cm
D.
4cm或6cm
C
提示:先根据题意画出图形,再分两种情况:①点P在线段AB上,②点P在线段AB上的延长线上,求出AP的长。
6.
已知点C在线段AB上,不能确定点C是AB的中点的
条件
是
(
)
C.
AC+CB=AB
D.
A.
AC=CB
B.
AB∶CB=2∶1
C
7.
用尺规作图:如图,已知线段a,b,c(b>a),作一条线段AB,使AB的长等于b-a+c.
(不写作法,保留作图痕迹)
a
b
c
8.
填空:
(1)把20.65°化成用度、分、秒表示的角度是
;
(2)把110°39′36″用度表示是
;
(3)计算90°38′54″+10°24′14″=
;
(4)78°40′
的补角是
.
20°39′
110.66°
100°3′8″
101°20′
9.
如图,在三角形中,∠C=90°,∠A=46°30′,则
∠B的度数是
(
)
A.
43°30′
B.
44°30′
C.
43°70′
D.
44°70′
A
C
B
A
10.
(易错题)已知∠AOB=60°,∠BOC=36°,则∠AOC
的度数等于
.
11.
已知一个角的补角等于这个角的4倍,这个角的余角
的度数等于
.
24°或96°
54°
●能力提高题
12.
如图,点O是直线AB上一点,∠AOD,∠COE是
直角,与∠AOE互补的角为
。
A
O
B
C
D
E
∠BOE,∠COD
13.
如图,∠ACB=∠ACD=90°,则图中互为余角和相等
的锐角的对数分别有
(
)
A.
1,1
B.
2,2
C.
3,2
D.
4,2
A
B
C
D
D
14.
将一副三角尺按如图所示位置放置,若∠BCD=155°,
则∠ACE的度数为
。
25°
A
B
C
D
E
15.
如图,已知∠AOC是直角,OB是∠AOE的平分线,OD是
∠COE的平分线.
(1)当∠COE=32?时,
求∠BOD的度数.
(2)设∠COE=α,试说明:
∠BOD的大小与α的大小无关。
A
O
E
B
C
D
●综合运用题
1.
了解几何图形的分类,初步认识一些简单的图形。
2.
理解线段、射线、直线的关系,并能用恰当的方法表
示它们。掌握直线的基本事实。
3.
会比较线段的长度,用尺规作两条直线的和或差。能解决
与线段的中点有关。
4.
掌握角的有关概念及计算,余角和补角的性质及其应用;
4.
培养学生看图识图用图能力,体验数形结合思想.
几
何
图
形
立体
图形
平面
图形
直线
射线
线段
角
两点确定一条直线
长短比较
两点之间线段最短
度量与计算
大小比较
余角与补角
角平分线
同角(等角)的余角相等;
同角(等角)的补角相等.
1、几何图形包括立体图形和平面图形。我们学过的立体图
形有圆柱、
,圆锥、
和球。
要点复习
2、线段有2个端点,射线有1个端点,直线没有端点。将线
段向一个方向延长形成
,向两个相反的方向延
长形成
.
棱柱
棱锥
3、过
有且只有一条直线。即
确定一条直线。
射线
直线
两点
线段
4、两点之间的所有连线中,
最短.
两点
6、比较两个角的大小的方法有
和
。
7、如图,点B是AC的中点,线段AB、BC、AC的大小关
系是
。
5、比较线段长短的方法有
和
.
度量法
截取法
度量法
叠合法
8、以一个角的顶点为端点的一条射线,如果把这个角分成
,那么这条射线叫做这个角的平分线.
如图,若OC是∠AOB的平分线,
则
。
两个相等的角
9、角的大小由角的始边绕顶点旋转到终边时的
的大
小决定,而与所画角的两边的长度
.
无关
旋转量
10、度量角的基本单位有度、分、秒。角度单位之间的进率
是
,即
60
60
60
11、如果两个角的和等于一个
,那么这两个角互为余角.
直角
12、如果两个角的和等于一个
,那么这两个角互为补角.
平角
13、同角或等角的余角
,同角或等角的补角
.
相等
相等
14、如果a=b,c=b,那么
.
这叫
.
a=c
等量代换
要点突破
(一)图形的认识
例1
下列立体图形中,是棱柱的是
(
)
A
B
C
D
A
变式题:
下面图形中,平面图形的个数有
(
)
A.
2
B.
3
C.
4
D.
5
B
要点突破
(二)线段、射线、直线的性质
例2
随着我国路桥修建技术的提高,现在我国设计的高速公路桥梁多、隧道多,从而缩短了路程。其依据是(
)
A.
两点确定一条直线
B.
直线比曲线短
C.
两点之间,线段最短
D.
两条直线相交于一点
经过两点,确定一条直线
变式题1:砖匠师傅砌墙时,先将两端固定拉线,再沿着线砌墙,其原理是
.
C
变式题2:
下列说法正确的有
(
)
①射线的长度是直线长度的一半
②将射线AO反向无限延长得到直线OA
③右图中的线段共有3条
④在体育课排队时,体育老师在每一列取两个点,则经过
这两点可以画出唯一的一条直线
A.
①②
B.
②③
C.①③
D.
②④
D
要点突破
(三)线段的有关计算
例3
解:因为点D是AC的中点,AD=2.5cm,所以AC=2DC=5cm,DC=AD=2.5cm,从而BC=2DC=5cm.
所以,AB=2AC=10cm.
如图,已知点D是AC的中点,BC=2DC,AD=2.5cm,
求线段AB的长.
变式题:如图,已知
,E,F分别是AB,BC的中点,EF=7,求线段AB,DC的长.
A
D
C
B
E
F
A
D
C
B
E
F
提示:由
可得AB=3BD,BC=4BD,由E,F分别是AB,BC的中点,可得
求出BD=2,即可求出AB,DC的长。
要点突破
(四)角的有关计算
例4
解:因为∠DOC是∠D的余角,且∠D=60°,所以∠DOC=90°-60°=30°,又∠BOC=15°,所以,∠α=∠DOC-
∠BOC=30°-15°=15°.
因为∠AOD是∠α的余角,所以,
∠AOD=90°-15°=75°.
如图,将一副三角尺按如图位置放置,∠D=60°,量得∠BOC=15°,求∠α,∠AOD的度数.
变式题:
如图,点O是直线AB上的一点,OD平分∠AOC,OE
平分∠BOC,求∠DOE的度数.
A
O
D
B
C
E
要点突破
(五)简单作图题
例5
如图,已知线段AB=6,按以下要求完成作图并计算.
(1)延长线段AB,使BC=2AB(用圆规截取,保留作图痕迹);
(2)取线段AC的中点D,求出线段DB的长。
A
B
A
B
C
D
解:(1)如图所示:
(2)
BC=2AB=2×6=12,AC=AB+BC=6+12=18.
因为点D是AC的中点,所以AD=9,BD=AD-AB=3.
1.
图(a)中线段和射线的条数分别是
(
)
A.
2,2
B.
2,4
C.
3,4
D.
3,6
A
B
C
2.
图(b)小于平角的角共有
个,其中可用一个大写字母表示的角是
.
A
D
B
C
(a)
(b)
D
7
●基础巩固题
∠B,∠C
3.
如图,线段AB=6cm,点C是AB的中点,点D是AC的中点,
则线段DC的长为
cm.
4.
如图,线段AB=10cm,AD=2.5cm,点D是线段AC的中点,则线段BC的长为
cm.
1.5
5
5.
(易错题)已知线段AB=8cm,直线上有一点C,且BC=4cm,点P线段是AC的中点,则AP的长为
(
)
A.
2cm
B.
4cm
C.
2cm或6cm
D.
4cm或6cm
C
提示:先根据题意画出图形,再分两种情况:①点P在线段AB上,②点P在线段AB上的延长线上,求出AP的长。
6.
已知点C在线段AB上,不能确定点C是AB的中点的
条件
是
(
)
C.
AC+CB=AB
D.
A.
AC=CB
B.
AB∶CB=2∶1
C
7.
用尺规作图:如图,已知线段a,b,c(b>a),作一条线段AB,使AB的长等于b-a+c.
(不写作法,保留作图痕迹)
a
b
c
8.
填空:
(1)把20.65°化成用度、分、秒表示的角度是
;
(2)把110°39′36″用度表示是
;
(3)计算90°38′54″+10°24′14″=
;
(4)78°40′
的补角是
.
20°39′
110.66°
100°3′8″
101°20′
9.
如图,在三角形中,∠C=90°,∠A=46°30′,则
∠B的度数是
(
)
A.
43°30′
B.
44°30′
C.
43°70′
D.
44°70′
A
C
B
A
10.
(易错题)已知∠AOB=60°,∠BOC=36°,则∠AOC
的度数等于
.
11.
已知一个角的补角等于这个角的4倍,这个角的余角
的度数等于
.
24°或96°
54°
●能力提高题
12.
如图,点O是直线AB上一点,∠AOD,∠COE是
直角,与∠AOE互补的角为
。
A
O
B
C
D
E
∠BOE,∠COD
13.
如图,∠ACB=∠ACD=90°,则图中互为余角和相等
的锐角的对数分别有
(
)
A.
1,1
B.
2,2
C.
3,2
D.
4,2
A
B
C
D
D
14.
将一副三角尺按如图所示位置放置,若∠BCD=155°,
则∠ACE的度数为
。
25°
A
B
C
D
E
15.
如图,已知∠AOC是直角,OB是∠AOE的平分线,OD是
∠COE的平分线.
(1)当∠COE=32?时,
求∠BOD的度数.
(2)设∠COE=α,试说明:
∠BOD的大小与α的大小无关。
A
O
E
B
C
D
●综合运用题
同课章节目录
