八年级平行四边形专题练习(含答案)
图片预览
文档简介
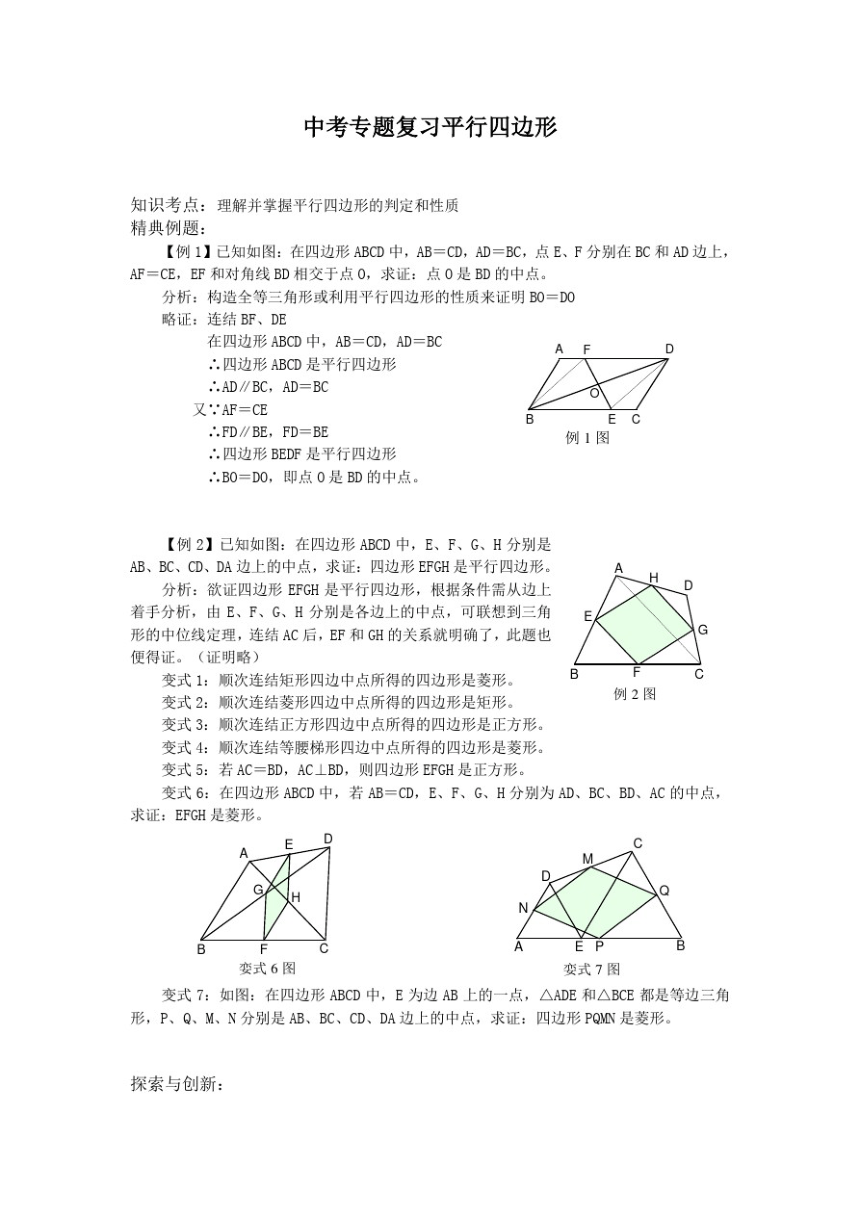
中考专题复习平行四边形
知识考点:理解并掌握平行四边形的判定和性质
精典例题:
【例1】已知如图:在四边形ABCD中,AB=CD,AD=BC,点E、F分别在BC和AD边上,
F=CE,EF和对角线BD相交于点0,求证:点0是BD的中点。
分析:构造全等三角形或利用平行四边形的性质来证明B0=D0
略证:连结BF、DE
在四边形ABCD中,AB=CD,AD=BC
∴四边形ABCD是平行四边形
∴AD∥BC,AD=BC
又∵AF=CE
E
C
∴FD∥BE,FD=BE
例1图
∴四边形BEDF是平行四边形
∴B0=D0,即点0是BD的中点
【例2】已知如图:在四边形ABCD中,E、F、G、H分别是
AB、BC、CD、DA边上的中点,求证:四边形EFGH是平行四边形。
分析:欲证四边形EFGH是平行四边形,根据条件需从边上
D
着手分析,由E、F、G、H分别是各边上的中点,可联想到三角E
形的中位线定理,连结AC后,EF和阻H的关系就明确了,此题也
XG
便得证。(证明略)
变式1:顺次连结矩形四边中点所得的四边形是菱形。
变式2:顺次连结菱形四边中点所得的四边形是矩形。
例2图
变式3:顺次连结正方形四边中点所得的四边形是正方形。
变式4:顺次连结等腰梯形四边中点所得的四边形是菱形。
变式5:若AC=BD,AC⊥BD,则四边形EFGH是正方形。
变式6:在四边形ABCD中,若AB=CD,E、F、G、H分别为AD、BC、BD、AC的中点,
求证:EFGH是菱形。
Q
娈式6图
娈式7图
变式7:如图:在四边形ABCD中,E为边AB上的一点,△ADE和△BCE都是等边三角
形,P、Q、M、N分别是AB、BC、CD、DA边上的中点,求证:四边形PQMN是菱形。
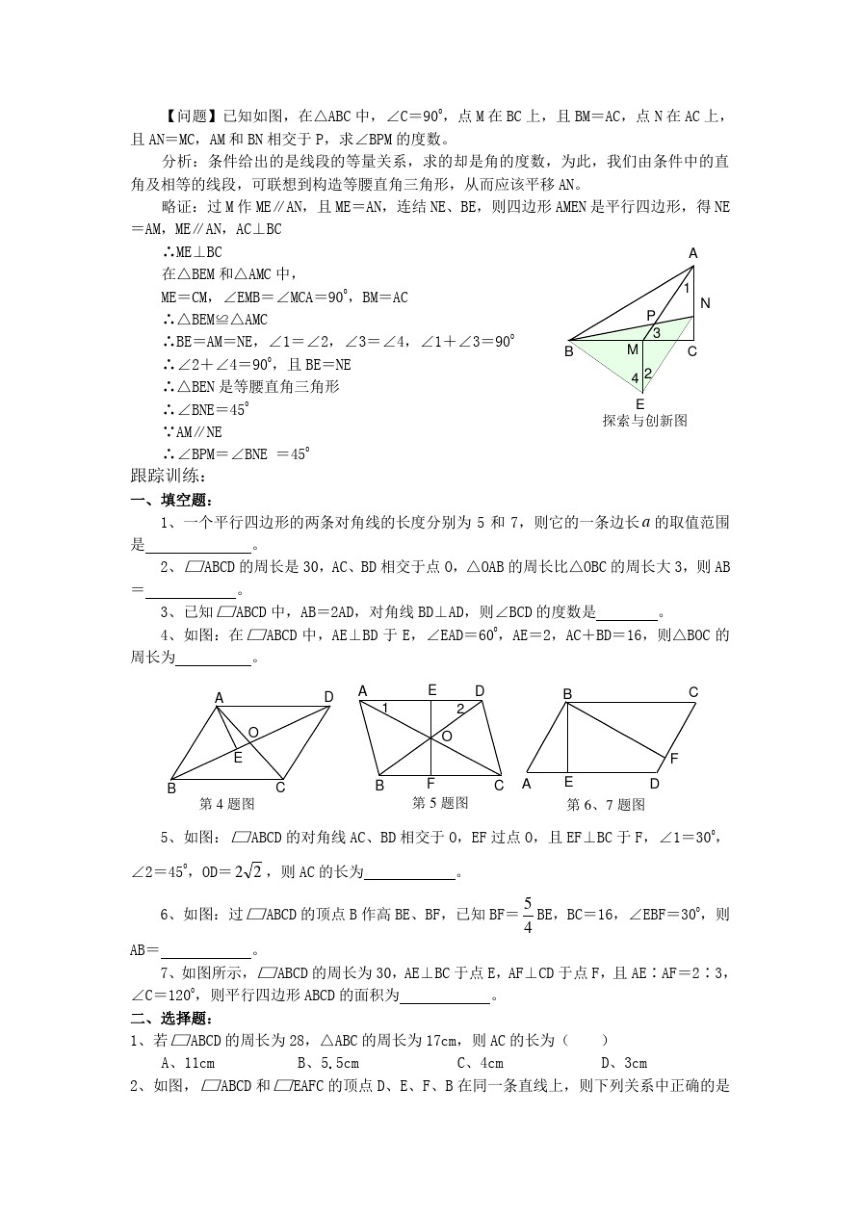
探索与创新
【问题】已知如图,在△ABC中,∠C=90°,点M在BC上,且BM=AC,点N在AC上,
且AN=MC,AM和BN相交于P,求∠BM的度数。
分析:条件给出的是线段的等量关系,求的却是角的度数,为此,我们由条件中的直
角及相等的线段,可联想到构造等腰直角三角形,从而应该平移AN。
略证:过M作M∥AN,且ME=AN,连结NE、BE,则四边形AEN是平行四边形,得NE
=AM,ME∥AN,AC⊥BC
∴ME⊥BC
在△BEM和△AMC中,
ME=CM,∠EMB=∠MCA=90,BM=AC
∴△BEM≌△AMC
∴BE=AM=NE,∠1=∠2,∠3=∠4,∠1+∠3=90
∴∠2+∠4=90°,且BE=NE
2
△BEN是等腰直角三角形
∠BNE=45°
探索与创新图
∵AM∥NE
∴∠BPM=∠BNE=45°
跟踪训练
、填空题:
一个平行四边形的两条对角线的长度分别为5和7,则它的一条边长a的取值范围
2、□ABCD的周长是30,AC、BD相交于点0,△OAB的周长比△OBC的周长大3,则AB
3、已知□ABCD中,AB=2AD,对角线BD⊥AD,则∠BCD的度数是
4、如图:在□ABCD中,AE⊥BD于E,∠EAD=60,AE=2,AC+BD=16,则△BOC的
周长为
D
C
第4题图
第5题图
第6、7题图
5、如图:□ABCD的对角线AC、BD相交于0,EF过点0,且EF⊥BC于F,∠1=30°,
∠2=45°,0D=2√2,则AC的长为
6、如图:过□ABCD的顶点B作高BE、BF,已知BF=BE,BC=16,∠EBF=30°,则
4
B
7、如图所示,□ABCD的周长为30,AE⊥BC于点E,AF⊥CD于点F,且AE:AF=2:
∠C=120°,则平行四边形ABCD的面积为
选择题
1、若□ABCD的周长为28,△ABC的周长为17cm,则AC的长为(
A、11cm
B、5.5cm
C、4cm
D、3cm
2、如图,□ABCD和□EAFC的顶点D、E、F、B在同一条直线上,则下列关系中正确的是
知识考点:理解并掌握平行四边形的判定和性质
精典例题:
【例1】已知如图:在四边形ABCD中,AB=CD,AD=BC,点E、F分别在BC和AD边上,
F=CE,EF和对角线BD相交于点0,求证:点0是BD的中点。
分析:构造全等三角形或利用平行四边形的性质来证明B0=D0
略证:连结BF、DE
在四边形ABCD中,AB=CD,AD=BC
∴四边形ABCD是平行四边形
∴AD∥BC,AD=BC
又∵AF=CE
E
C
∴FD∥BE,FD=BE
例1图
∴四边形BEDF是平行四边形
∴B0=D0,即点0是BD的中点
【例2】已知如图:在四边形ABCD中,E、F、G、H分别是
AB、BC、CD、DA边上的中点,求证:四边形EFGH是平行四边形。
分析:欲证四边形EFGH是平行四边形,根据条件需从边上
D
着手分析,由E、F、G、H分别是各边上的中点,可联想到三角E
形的中位线定理,连结AC后,EF和阻H的关系就明确了,此题也
XG
便得证。(证明略)
变式1:顺次连结矩形四边中点所得的四边形是菱形。
变式2:顺次连结菱形四边中点所得的四边形是矩形。
例2图
变式3:顺次连结正方形四边中点所得的四边形是正方形。
变式4:顺次连结等腰梯形四边中点所得的四边形是菱形。
变式5:若AC=BD,AC⊥BD,则四边形EFGH是正方形。
变式6:在四边形ABCD中,若AB=CD,E、F、G、H分别为AD、BC、BD、AC的中点,
求证:EFGH是菱形。
Q
娈式6图
娈式7图
变式7:如图:在四边形ABCD中,E为边AB上的一点,△ADE和△BCE都是等边三角
形,P、Q、M、N分别是AB、BC、CD、DA边上的中点,求证:四边形PQMN是菱形。
探索与创新
【问题】已知如图,在△ABC中,∠C=90°,点M在BC上,且BM=AC,点N在AC上,
且AN=MC,AM和BN相交于P,求∠BM的度数。
分析:条件给出的是线段的等量关系,求的却是角的度数,为此,我们由条件中的直
角及相等的线段,可联想到构造等腰直角三角形,从而应该平移AN。
略证:过M作M∥AN,且ME=AN,连结NE、BE,则四边形AEN是平行四边形,得NE
=AM,ME∥AN,AC⊥BC
∴ME⊥BC
在△BEM和△AMC中,
ME=CM,∠EMB=∠MCA=90,BM=AC
∴△BEM≌△AMC
∴BE=AM=NE,∠1=∠2,∠3=∠4,∠1+∠3=90
∴∠2+∠4=90°,且BE=NE
2
△BEN是等腰直角三角形
∠BNE=45°
探索与创新图
∵AM∥NE
∴∠BPM=∠BNE=45°
跟踪训练
、填空题:
一个平行四边形的两条对角线的长度分别为5和7,则它的一条边长a的取值范围
2、□ABCD的周长是30,AC、BD相交于点0,△OAB的周长比△OBC的周长大3,则AB
3、已知□ABCD中,AB=2AD,对角线BD⊥AD,则∠BCD的度数是
4、如图:在□ABCD中,AE⊥BD于E,∠EAD=60,AE=2,AC+BD=16,则△BOC的
周长为
D
C
第4题图
第5题图
第6、7题图
5、如图:□ABCD的对角线AC、BD相交于0,EF过点0,且EF⊥BC于F,∠1=30°,
∠2=45°,0D=2√2,则AC的长为
6、如图:过□ABCD的顶点B作高BE、BF,已知BF=BE,BC=16,∠EBF=30°,则
4
B
7、如图所示,□ABCD的周长为30,AE⊥BC于点E,AF⊥CD于点F,且AE:AF=2:
∠C=120°,则平行四边形ABCD的面积为
选择题
1、若□ABCD的周长为28,△ABC的周长为17cm,则AC的长为(
A、11cm
B、5.5cm
C、4cm
D、3cm
2、如图,□ABCD和□EAFC的顶点D、E、F、B在同一条直线上,则下列关系中正确的是
