19.2有趣的几何 课件(共25张PPT)
文档属性
| 名称 | 19.2有趣的几何 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
有趣的几何
在初一的几何课中,我们已经接触到了命题与证明,进入初二以后,证明题逐渐复杂起来,几何证明题对于培养我们的逻辑思维能力,推理论证能力是非常有好处的.
要做对一道几何证明题,不但要对题目所涉及的知识能了如指掌,熟练掌握,还要求掌握正确的证明方法.
证明是一种思维过程,是从一些已知或已证的真命题推出新命题正确性的过程.
几何证明就是用逻辑推理的方法论证图形的几何性质,每步推理都要以所给的条件、定义、公理或已经证明的定理为依据.
一个命题的证明过程本身是由一系列相互联系的推理来完成的,一个证明是正确的,则证明过程的各步推理都必须是正确的.
数学证明按其方式可分为直接证明与间接证明.
从题目的条件出发,根据定义、公理、定理等,通过一系列的逻辑推理,一直推导到所要证的结论为止,这种从题目的条件人手,从正面肯定结论的证明方法,叫做直接证明.
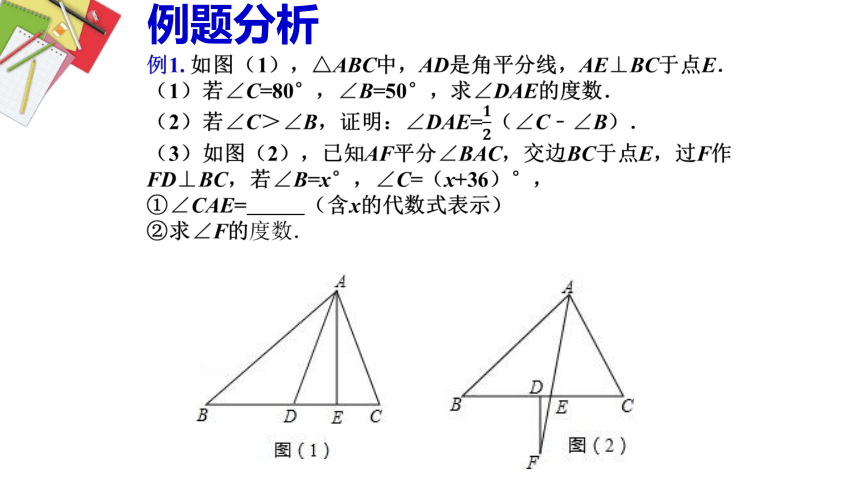
例题分析
1
?
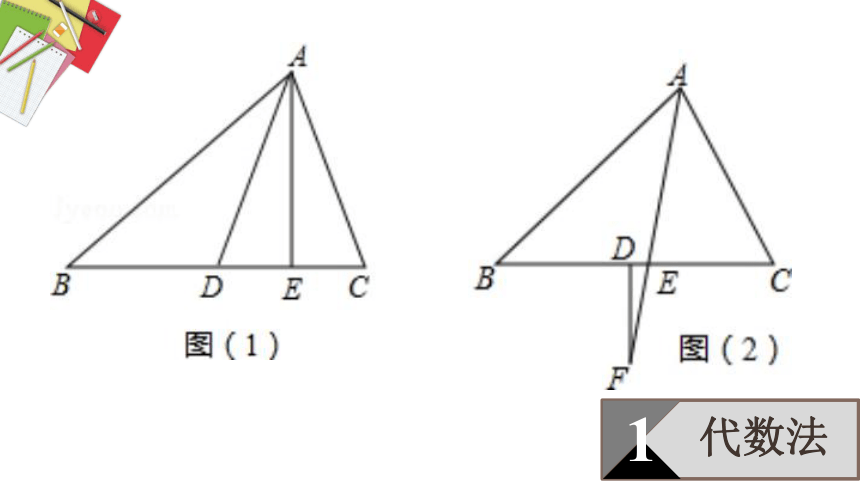
例题分析
1
代数法
例题小结
(1)三角形一个内角的平分线与这个角对边上的高所形成的夹角等于另两个角之差的一半(当高在三角形外部时也成立).
(2)代数法是指用代数知识来解决几何问题的方法,也就是运用几何定理、法则,通过列方程、方程组或不等式及解方程、方程组、恒等变形等代数知识,把几何问题转化为代数问题来解决的方法.
常用的几何知识有三角形内角和定理、外角定理、勾股定理、三角形面积公式等.
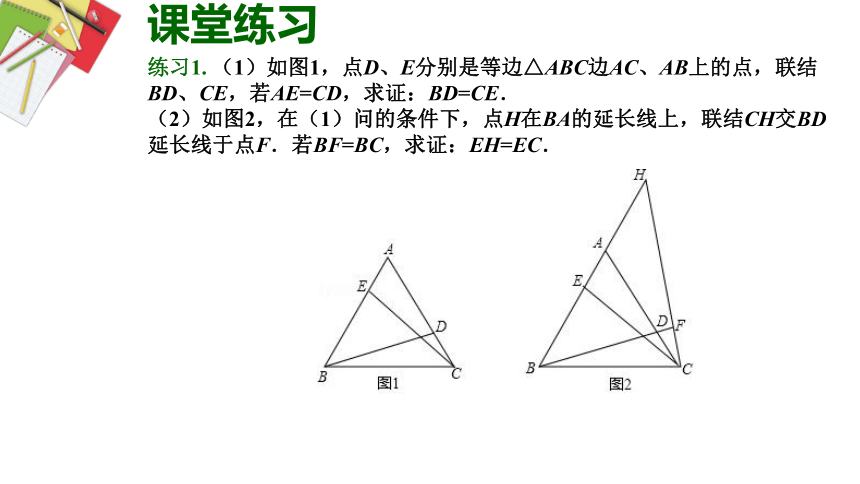
课堂练习
1
练习1.
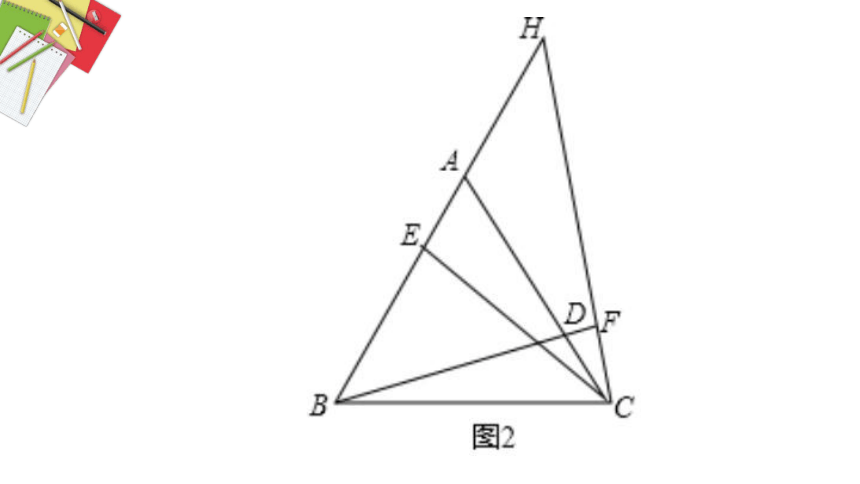
(1)如图1,点D、E分别是等边△ABC边AC、AB上的点,联结BD、CE,若AE=CD,求证:BD=CE.
(2)如图2,在(1)问的条件下,点H在BA的延长线上,联结CH交BD延长线于点F.若BF=BC,求证:EH=EC.
课堂练习
例题分析
2
例2.
P是△ABC中∠A的平分线上的任意一点,过C作CE//PB,交AB的延长线于E,过B作BF//PC,交AC的延长线于F,联结PE、PF.
求证:BE=CF.
例题分析
2
面积法
例题小结
(1)在平面几何题中,由于两个三角形、四边形的面积比,往往可以等于两线段乘积的比,或两条对应线段的平方比,或两条线段的比,这就是说,某些证线段相等(包括线段倍分及和差关系)的题,可以先转化为面积比,再转化为某些线段的比,从而以面积为媒介,沟通了线段间的关系,用等积和面积比的方法证明了几何题,这就是面积法.
(2)用面积法证明几何题时,常用的公理、定理有:
①一个平面图形的面积,等于把它分割成的所有图形的面积之和;
②全等形的面积相等;
③两个三角形(或平行四边形)的面积比等于底与相应高的积之比;
④等底三角形(或平行四边形)的面积比等于相应高之比;
⑤等高三角形(或平行四边形)的面积比等于相应底之比.
课堂练习
2
练习2.已知△ABC中,∠ACB=
90°,CE平分∠ACB,交AB于E,EF⊥AC于F,求证:
课堂练习
课堂小结
3
通过这节课你学习到了哪些证(解)几何题的方法?
证(解)几何题时,有哪些应注意的问题?
课堂
小结
作业布置
4
必做:完成《习题精炼》
选做:完成《拓展提高》
课后思考
5
思考1.
证明:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例(三角形内角平分线性质定理2).
如图(1),已知△ABC中,AD是角平分线,
求证:
.
思考2.
如图(2),已知△ABC中,BD、CE分别为∠B、∠C的平分线,又BE=CD.求证:AB=
AC.
课后思考
思考3.
已知△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
(1)探究:如图①,当点A在边EC上,点C在线段BD上时,联结BE、AD.求证:BE=AD,BE⊥AD.
(2)拓展:如图②,当点A在边DE上时,AB、CE交于点F,联结BE.若AE=2,AD=4,求EF的长.
课后思考
手拉手模型
谢谢大家!
Thanks
Merci
Gracias
有趣的几何
在初一的几何课中,我们已经接触到了命题与证明,进入初二以后,证明题逐渐复杂起来,几何证明题对于培养我们的逻辑思维能力,推理论证能力是非常有好处的.
要做对一道几何证明题,不但要对题目所涉及的知识能了如指掌,熟练掌握,还要求掌握正确的证明方法.
证明是一种思维过程,是从一些已知或已证的真命题推出新命题正确性的过程.
几何证明就是用逻辑推理的方法论证图形的几何性质,每步推理都要以所给的条件、定义、公理或已经证明的定理为依据.
一个命题的证明过程本身是由一系列相互联系的推理来完成的,一个证明是正确的,则证明过程的各步推理都必须是正确的.
数学证明按其方式可分为直接证明与间接证明.
从题目的条件出发,根据定义、公理、定理等,通过一系列的逻辑推理,一直推导到所要证的结论为止,这种从题目的条件人手,从正面肯定结论的证明方法,叫做直接证明.
例题分析
1
?
例题分析
1
代数法
例题小结
(1)三角形一个内角的平分线与这个角对边上的高所形成的夹角等于另两个角之差的一半(当高在三角形外部时也成立).
(2)代数法是指用代数知识来解决几何问题的方法,也就是运用几何定理、法则,通过列方程、方程组或不等式及解方程、方程组、恒等变形等代数知识,把几何问题转化为代数问题来解决的方法.
常用的几何知识有三角形内角和定理、外角定理、勾股定理、三角形面积公式等.
课堂练习
1
练习1.
(1)如图1,点D、E分别是等边△ABC边AC、AB上的点,联结BD、CE,若AE=CD,求证:BD=CE.
(2)如图2,在(1)问的条件下,点H在BA的延长线上,联结CH交BD延长线于点F.若BF=BC,求证:EH=EC.
课堂练习
例题分析
2
例2.
P是△ABC中∠A的平分线上的任意一点,过C作CE//PB,交AB的延长线于E,过B作BF//PC,交AC的延长线于F,联结PE、PF.
求证:BE=CF.
例题分析
2
面积法
例题小结
(1)在平面几何题中,由于两个三角形、四边形的面积比,往往可以等于两线段乘积的比,或两条对应线段的平方比,或两条线段的比,这就是说,某些证线段相等(包括线段倍分及和差关系)的题,可以先转化为面积比,再转化为某些线段的比,从而以面积为媒介,沟通了线段间的关系,用等积和面积比的方法证明了几何题,这就是面积法.
(2)用面积法证明几何题时,常用的公理、定理有:
①一个平面图形的面积,等于把它分割成的所有图形的面积之和;
②全等形的面积相等;
③两个三角形(或平行四边形)的面积比等于底与相应高的积之比;
④等底三角形(或平行四边形)的面积比等于相应高之比;
⑤等高三角形(或平行四边形)的面积比等于相应底之比.
课堂练习
2
练习2.已知△ABC中,∠ACB=
90°,CE平分∠ACB,交AB于E,EF⊥AC于F,求证:
课堂练习
课堂小结
3
通过这节课你学习到了哪些证(解)几何题的方法?
证(解)几何题时,有哪些应注意的问题?
课堂
小结
作业布置
4
必做:完成《习题精炼》
选做:完成《拓展提高》
课后思考
5
思考1.
证明:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例(三角形内角平分线性质定理2).
如图(1),已知△ABC中,AD是角平分线,
求证:
.
思考2.
如图(2),已知△ABC中,BD、CE分别为∠B、∠C的平分线,又BE=CD.求证:AB=
AC.
课后思考
思考3.
已知△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
(1)探究:如图①,当点A在边EC上,点C在线段BD上时,联结BE、AD.求证:BE=AD,BE⊥AD.
(2)拓展:如图②,当点A在边DE上时,AB、CE交于点F,联结BE.若AE=2,AD=4,求EF的长.
课后思考
手拉手模型
谢谢大家!
Thanks
Merci
Gracias
