第十五章 分式计算、解方程、化简求值专题练习(含答案)
文档属性
| 名称 | 第十五章 分式计算、解方程、化简求值专题练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 509.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 15:05:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级数学第十五章分式计算、解方程、化简求值专题练习
一、计算
1、﹣|﹣3|+﹣(﹣2020
)0+
2、+|﹣|+()0.
3、.
4、()0+()-1--|-1|
(
-2;)
5、
6、(2-1)0+|-6|-8×4-1+.
7、
8、计算-2
二、解分式方程
9、=1-;
10、=-1;
11、+=;
12、+=.
13、
+=1;
14、+=1;
15、+1=.
16、.
三、化简求值
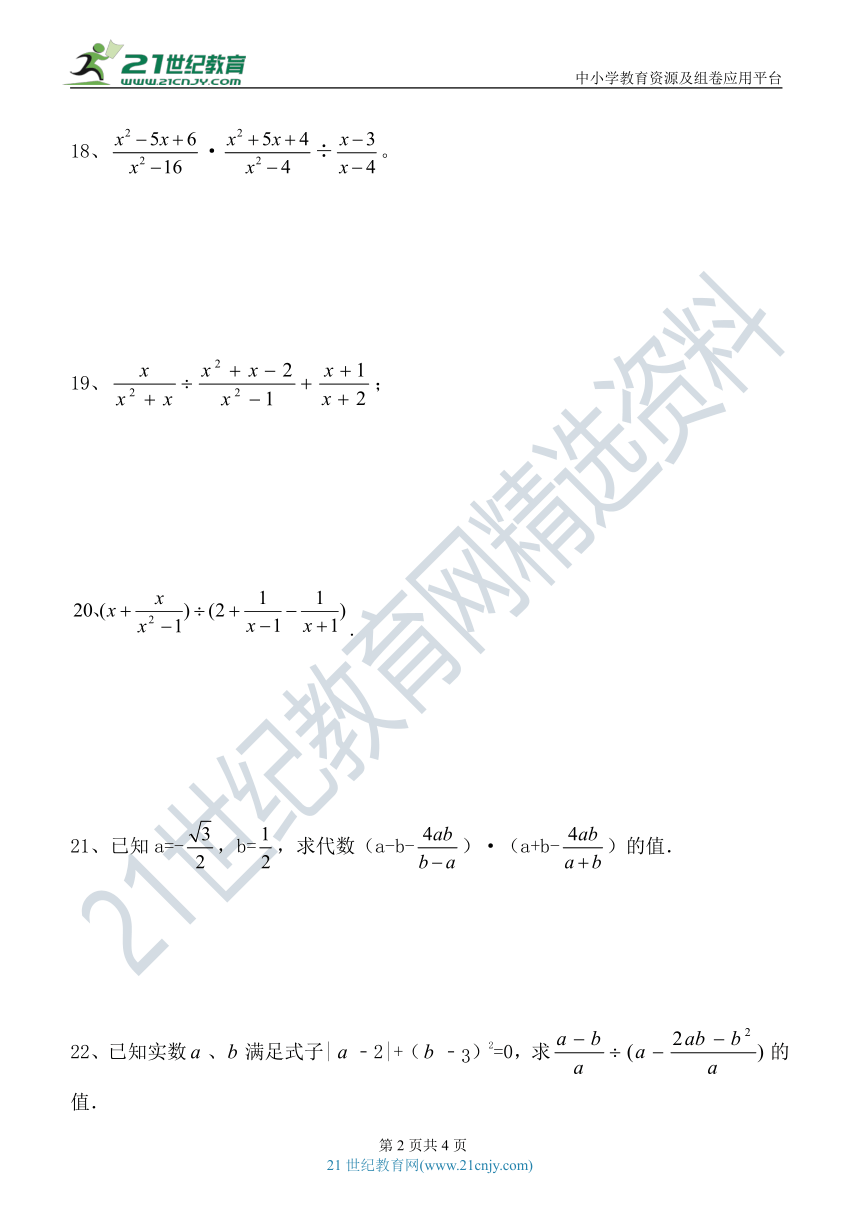
17、化简·÷;
18、·÷。
19、;
.
21、已知a=-,b=,求代数(a-b-)·(a+b-)的值.
22、已知实数、满足式子|﹣2|+(﹣3)2=0,求的值.
23、先化简,再求值:,其中是不等式3+7>1的负整数解.
25、
已知.试说明不论为何使分式有意义
的值,y的值不变.
26、若x2-3x+1=0,求x2+的值.
27、已知=+,求+的值.
28、若x:y:z=2:4:6,求的值.
人教版八年级数学第十五章分式计算、解方程、化简求值专题练习
答案与解析
一、计算
1.
2.
2
3.10
4.
5.-400
6.
9
7.-4
8.-4
二、解分式方程
9、=1-;
解:方程两边同乘以(x-2),得
2x=x-2+1.解得x=-1.
经检验,x=-1是原方程的解.
10、=-1;
解:方程两边同乘以(x-2)(x+3),得
6(x+3)=x(x-2)-(x-2)(x+3).
解得x=-.
经检验,x=-是原方程的解.
11、+=;
解:方程两边都乘以(x+2)(x-2),得
x+2(x-2)=x+2.解得x=3.
经检验,x=3是原方程的解.
12、+=.
解:方程两边同乘以9x-3,得
2(3x-1)+3x=1.解得x=.
检验:当x=时,9x-3=0.
因此x=不是原方程的解.
∴原分式方程无解.
13、
+=1;
解:去分母,得3+x(x+3)=x2-9,
3+x2+3x=x2-9.解得x=-4.
经检验,x=-4是原方程的解.
14、+=1;
解:方程两边同乘以(x+1)(x-1),得
(x+1)2+4=(x+1)(x-1),
解得x=-3.
检验:当x=-3时,(x+1)(x-1)≠0,
∴x=-3是原方程的解.
∴原方程的解是x=-3.
15、+1=.
解:原方程可化为+1=.
去分母,得8+(x+2)(x-2)=x(x+2).
解得x=2.
检验:当x=2时,(x+2)(x-2)=0,
∴x=2是原方程的增根,即原方程无解.
16、.
【过程书写】
检验:把x=2代入原方程,不成立
∴x=2是原分式方程的增根
∴原分式方程无解
三、化简求值
17、化简·÷;
原式=··=a+5
18、·÷。
原式=··=
19、;
原式=
=.
20、.
原式=
=
=
=.
21、已知a=-,b=,求代数(a-b-)·(a+b-)的值.
解:原式=(+)(-)
=·=·=(a+b)(a-b)=a2-b2
当a=-,b=时,
原式=(-)2-()2=-=.
22、
已知实数、满足式子|﹣2|+(﹣3)2=0,求的值.
解:原式=
=,
=,
∵|﹣2|+(﹣3)2=0,
∴﹣2=0,﹣3=0,
解得=2,=3
所以,原式=-1
23、先化简,再求值:,其中是不等式3+7>1的负整数解.
原式=[]×,
=,
=,
=,
>1,
>﹣6,
>﹣2,
∵是不等式>1的负整数解,
∴=﹣1
把=﹣1代入中得:=3.
24、先化简,然后在﹣1、1、2三个数中任选一个合适的数代入求值.
.解:原式=
=,
当=2时,原式==5.
26、
已知.试说明不论为何使分式有意义
的值,y的值不变.
=-
=
=1,
所以不论为何使分式有意义的值,的值不变,都为1.
26、若x2-3x+1=0,求x2+的值.
由x2-3x+1=0两边同除以x得x-3+=0
x+=3,x2++2=9
∴x2+=7
27、已知=+,求+的值.
解:由已知得=
∴(a+b)2=ab
∴+====-1
28、若x:y:z=2:4:6,求的值.
解:由已知设x=2k,则y=4k,z=6k
代入原式===-
PAGE
21世纪教育网
www.21cnjy.com
精品试卷·第
页
(共
2
页)
第2页共4页
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级数学第十五章分式计算、解方程、化简求值专题练习
一、计算
1、﹣|﹣3|+﹣(﹣2020
)0+
2、+|﹣|+()0.
3、.
4、()0+()-1--|-1|
(
-2;)
5、
6、(2-1)0+|-6|-8×4-1+.
7、
8、计算-2
二、解分式方程
9、=1-;
10、=-1;
11、+=;
12、+=.
13、
+=1;
14、+=1;
15、+1=.
16、.
三、化简求值
17、化简·÷;
18、·÷。
19、;
.
21、已知a=-,b=,求代数(a-b-)·(a+b-)的值.
22、已知实数、满足式子|﹣2|+(﹣3)2=0,求的值.
23、先化简,再求值:,其中是不等式3+7>1的负整数解.
25、
已知.试说明不论为何使分式有意义
的值,y的值不变.
26、若x2-3x+1=0,求x2+的值.
27、已知=+,求+的值.
28、若x:y:z=2:4:6,求的值.
人教版八年级数学第十五章分式计算、解方程、化简求值专题练习
答案与解析
一、计算
1.
2.
2
3.10
4.
5.-400
6.
9
7.-4
8.-4
二、解分式方程
9、=1-;
解:方程两边同乘以(x-2),得
2x=x-2+1.解得x=-1.
经检验,x=-1是原方程的解.
10、=-1;
解:方程两边同乘以(x-2)(x+3),得
6(x+3)=x(x-2)-(x-2)(x+3).
解得x=-.
经检验,x=-是原方程的解.
11、+=;
解:方程两边都乘以(x+2)(x-2),得
x+2(x-2)=x+2.解得x=3.
经检验,x=3是原方程的解.
12、+=.
解:方程两边同乘以9x-3,得
2(3x-1)+3x=1.解得x=.
检验:当x=时,9x-3=0.
因此x=不是原方程的解.
∴原分式方程无解.
13、
+=1;
解:去分母,得3+x(x+3)=x2-9,
3+x2+3x=x2-9.解得x=-4.
经检验,x=-4是原方程的解.
14、+=1;
解:方程两边同乘以(x+1)(x-1),得
(x+1)2+4=(x+1)(x-1),
解得x=-3.
检验:当x=-3时,(x+1)(x-1)≠0,
∴x=-3是原方程的解.
∴原方程的解是x=-3.
15、+1=.
解:原方程可化为+1=.
去分母,得8+(x+2)(x-2)=x(x+2).
解得x=2.
检验:当x=2时,(x+2)(x-2)=0,
∴x=2是原方程的增根,即原方程无解.
16、.
【过程书写】
检验:把x=2代入原方程,不成立
∴x=2是原分式方程的增根
∴原分式方程无解
三、化简求值
17、化简·÷;
原式=··=a+5
18、·÷。
原式=··=
19、;
原式=
=.
20、.
原式=
=
=
=.
21、已知a=-,b=,求代数(a-b-)·(a+b-)的值.
解:原式=(+)(-)
=·=·=(a+b)(a-b)=a2-b2
当a=-,b=时,
原式=(-)2-()2=-=.
22、
已知实数、满足式子|﹣2|+(﹣3)2=0,求的值.
解:原式=
=,
=,
∵|﹣2|+(﹣3)2=0,
∴﹣2=0,﹣3=0,
解得=2,=3
所以,原式=-1
23、先化简,再求值:,其中是不等式3+7>1的负整数解.
原式=[]×,
=,
=,
=,
>1,
>﹣6,
>﹣2,
∵是不等式>1的负整数解,
∴=﹣1
把=﹣1代入中得:=3.
24、先化简,然后在﹣1、1、2三个数中任选一个合适的数代入求值.
.解:原式=
=,
当=2时,原式==5.
26、
已知.试说明不论为何使分式有意义
的值,y的值不变.
=-
=
=1,
所以不论为何使分式有意义的值,的值不变,都为1.
26、若x2-3x+1=0,求x2+的值.
由x2-3x+1=0两边同除以x得x-3+=0
x+=3,x2++2=9
∴x2+=7
27、已知=+,求+的值.
解:由已知得=
∴(a+b)2=ab
∴+====-1
28、若x:y:z=2:4:6,求的值.
解:由已知设x=2k,则y=4k,z=6k
代入原式===-
PAGE
21世纪教育网
www.21cnjy.com
精品试卷·第
页
(共
2
页)
第2页共4页
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
