人教版小学数学五年级下册总复习课件(共63张)
文档属性
| 名称 | 人教版小学数学五年级下册总复习课件(共63张) |  | |
| 格式 | zip | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 18:08:38 | ||
图片预览









文档简介
(共63张PPT)
总复习课件
特殊情况
熟练掌握两种特殊情况。
两数关系
最大公因数
最小公倍数
互质关系
1
两数积
倍数关系
较小数
较大数
求三个数的最小公倍数的特殊规律:
当三个数两两互质时,最小公倍数是这三个数的积;
[2
,7,9]=
126
当三个数都成整倍数关系时,最大的数就是最小公倍数;
[18
,6,54]=
54
当三个数中有两个数成倍数关系时,那么求三个数的最小公倍数就可转化为求这两个数中较大者与第三个数的最小公倍数等。
[18
,6,27]
[18
,27]=108
易混概念对比
1.如果甲数是乙数的5倍,那么,乙数一定
是甲数的倍数。(
)
倍的概念比倍数要广,倍可以适用于小数、
分数和整数,而倍数只适用于整数。
例如:
16是8的2倍,也可以说16是8的倍数。
1.6是0.8的2倍,但是不能说1.6是0.8的倍数。
2.出示判断题:
(1)自然数中,除了奇数就是偶数。(
)
(2)所有的奇数都是质数。
(
)
(3)所有的合数都是偶数。
(
)
(4)自然数中,除了质数就是合数。(
)
(5)质数与质数的积还是质数。
(
)
(6)一个数越大,它的因数的个数就越多。
(
)
注意:奇数里既有质数也有合数还有1。
质数里除了2以外都是奇数。
偶数里除了2以外全是合数。
北京站是104路和103路电车的起发站。104路每3分发一次车,103路每8分发一次车,这两路电车同时发车以后,至少再过多少分又同时发车?
分析:104路电车每3分发一次车,每次发车时间一定是3的倍数,即第二次发车与第一次发车间隔3分,第三次发车与第一次发车间隔6分,而103路电车每8分发一次车,每次发车的时间一定是8的倍数,即第二次发车与第一次发车间隔8分,第三次发车与第一次发车间隔16分,这样就找到了每次两路电车同时发车的时间,就是求3和8的最小公倍数。
小红家的客厅长48分米,宽32分米。现在给客厅的地面铺正方形地砖,有三种砖,你帮小红家想一想,选择哪种地砖能铺得即整齐又不会有余料?
边长3分米
边长6分米
边长8分米
分析:求出48和32的公因数,这个公因数是地砖的边长。
复习长方体和正方体
第一课时
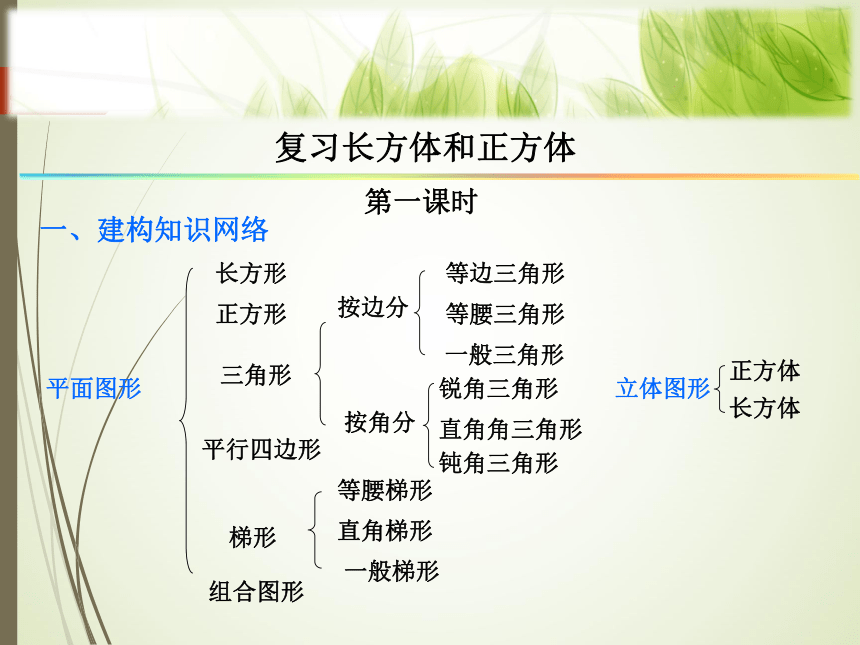
长方形
正方形
三角形
按边分
按角分
等边三角形
等腰三角形
一般三角形
锐角三角形
直角角三角形
钝角三角形
平行四边形
梯形
等腰梯形
直角梯形
一般梯形
组合图形
平面图形
一、建构知识网络
立体图形
正方体
长方体
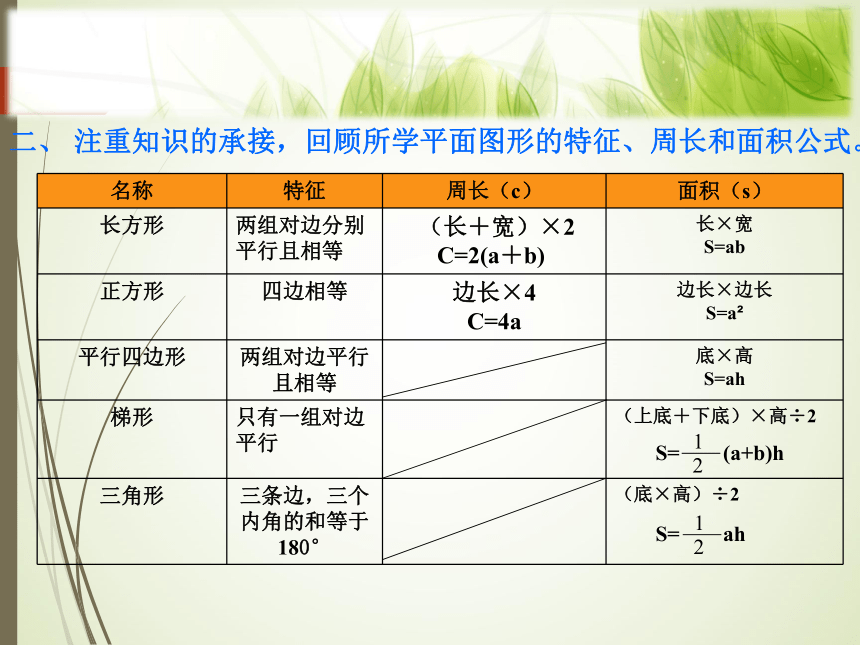
二、
注重知识的承接,回顾所学平面图形的特征、周长和面积公式。
名称
特征
周长(c)
面积(s)
长方形
两组对边分别平行且相等
(长+宽)×2
C=2(a+b)
长×宽
S=ab
正方形
四边相等
边长×4
C=4a
边长×边长
S=a?
平行四边形
两组对边平行且相等
底×高
S=ah
梯形
只有一组对边平行
(上底+下底)×高÷2
三角形
三条边,三个内角的和等于180°
(底×高)÷2
ah
S=
1
2
(a+b)h
S=
1
2
三、
明确长方体、正方体的异同。
从点、棱、面三方面比较长方体和正方体之间的相同点和不同点
长方体
正方体
相同点
6个面、12条棱、8个顶点
不同点
6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。
6个面都是正方形,
6个面完全相同
相对棱的长度相等
12条棱长度都相等
正方体是特殊的长方体。
用集合图表示:
长方体
正方体
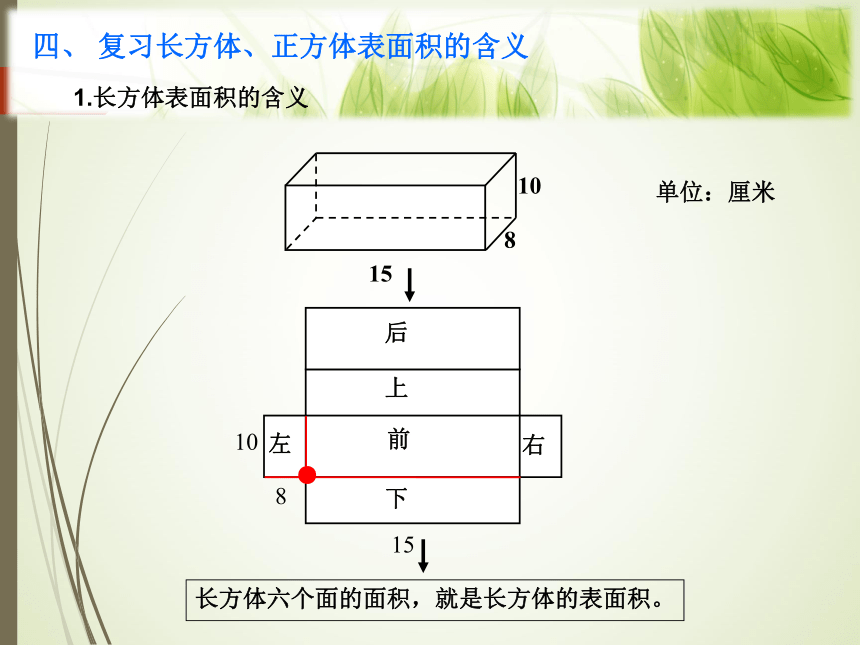
四、
复习长方体、正方体表面积的含义
15
10
8
后
前
上
下
左
右
●
15
10
8
单位:厘米
长方体六个面的面积,就是长方体的表面积。
1.长方体表面积的含义
2.正方体表面积的含义
(1)正方体棱长与每个面边长的关系
后
上
前
下
左
右
正方体展开图的每个面都是正方形,边长就是正方体的棱长,每个面的面积都等于棱长乘棱长。
五、复习长方体、正方体体积公式的推导
长方体的体积
=
长
×
宽
×
高
底面积
正方体的体积
=
棱长
×棱长×棱长
底面积
可看作是高
长方体(或正方体)的
体积
=
底面积
×
高
六、体积与容积区别与联系
异同点
体积
容积
区别
意义不同
物体所占空间的大小,叫做物体的体积。
一个容器所能容纳物体的体积,叫做这个容器的容积。
测量方法不同
从物体外部测量长、宽、高。
从容器里面测量长、宽、高。
单位名称不同
m?、dm?、cm?。
容积单位:L和ml;计量固体时用体积单位。
联系
容积的大小是通过所能容纳物体的体积表示出来的。
计算方法相同
7厘米
5厘米
5厘米
这个长方体的长是(
7
)厘米,宽是(
5
)厘米,高是(
5
)厘米,这个长方体有(
2
)个面是正方形,有(
4
)个面是长方形。
如图
1.
2.
要焊接一个长10cm,宽8cm,高6cm的长方体框架,要准备10cm,宽8cm,高6cm的铁丝各(
4
)根。
3.一个正方体纸盒的棱长是7cm,这个纸盒的棱长总和是(84
)cm。
4.有一根150cm长的铁丝,用这根铁丝焊成了一个正方体的框架,还剩铁丝6cm。这个正方体框架的棱长是(
)厘米。
七、基础知识的练习
150cm
12
8.有一个长方体,底面是一个正方形,高18cm,侧面展开正好是一个正方形。这个长方体的体积是(
)
cm?
。
18÷4=4.5(cm)
4.5×4.5×18
=20.25×18
=364.5(cm?)
18cm
18cm
18cm
10.把棱长是1厘米的小正方体拼摆在一起。如果从右面看,所看到的图形面积是(
)平方厘米,体积是(
)立方厘米。
7
11
11.
一个棱长为2cm的正方体,在它的一个角上挖掉一个棱长为1cm的小正方体,它的表面积是
(???
)cm?。
第二课时:解决相关的实际问题
12cm
15cm
8cm
1.
一条彩带捆扎一种礼盒(如图),如果
接头处的彩带长30cm,求这条彩带的长度。
8×4+12×2+15×2+30=116(cm)
答:这条彩带长116厘米。
2.与右面正方体一致的展开图是(
)。
B
1
2
3
1
2
3
2
3
1
1
2
3
C
B
A
甲
乙
取出石块后
2.1dm
1.8dm
3.
图中有两个完全一样的长方体水箱,水箱的底面积是2平方分米,请结合图中所给信息求出甲箱中石块的体积是多少?
2×(2.1-1.8)=0.6(dm?)
答:石块的体积是0.6dm?。
5厘米
5厘米
5厘米
5.把
积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
(25÷5)×(20÷5)×(20÷5)
=5×4×4
=80(块)
答:纸箱最多可容纳积木80块。
6.把
积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
5厘米
3厘米
3厘米
(25÷3)×(20÷3)×(20÷5)
≈8×6×4
=192(块)
答:纸箱最多可容纳积木192块。
7.一块长方形铁皮,长40cm,宽30cm,像下图这样从4个角各剪掉一个边长为5厘米的正方形,然后做成盒子,这个盒子的容积是多少升?
40cm
30cm
(40-5×2)×(30-5×2)×5=3000(cm?)
3000cm?=3L
答:这个盒子的容积是3升。
12ml=12cm3
24ml=24cm3
一个小球的体积:(24-12)
÷(4-1)=4(cm3)
一个大球的体积:12-4=8(cm3)
左图长、宽、高分别是4cm、3cm、3cm。
它的体积是:
4×3×3=36(cm2)
右图长、宽、高分别是4cm、3cm、4cm。
它的体积是:
4×3×4=48(cm2)
10.用3个长5cm,宽4cm,高3cm的长方体木块,拼成一个表面积最小的长方体。这个长方体的表面积是多少平方厘米?
5cm
4cm
3cm
[5×4+5×(3×3)+4×(3×3)]×2=(20+45+36)×2=202(cm?)
答:这个长方体的表面积是202平方厘米。
3cm
2cm
6cm
6cm
11.有一个形状如图的零件,由一个长方体和一个
正方体组合而成。长方体的长和宽都是6cm,高是3cm,正方体的棱长是2cm。求这个零件的表面积。
2×2×4+6×3×4+6×6×2
=16+72+72
=160(cm?)
答:这个零件的表面积是160平方厘米。
12.由27个棱长为1cm的小正方体组成一个棱长为3cm的大正方体,若自上而下去掉中间的3个小正方体(如图所示),则剩下的几何体的表面积是多少平方厘米?
3×3×6-1×1×2+3×1×4
=54-2+12
=64(cm?)
答:剩下的几何体的表面积是64平方厘米。
13.从一个大长方体上切下一个体积是128立方厘米的小长方体(如图)。原来大长方体的体积是多少立方厘米?
22cm
8cm
切下部分
128÷8×22
=16×22
=352(立方厘米)
答:原来大长方体的体积是352立方厘米。
14.
一个密封的长方体容器里面装有一些水,水深9厘米,如果把这个容器的右面做底,这时容器内的水深多少厘米?
36
10
12
36
10
12
36×10×9=3240(cm3)
3240÷(12×10)=27(cm)
答:容器内的水深27厘米。
分数
分数的意义
分数单位
分子分母的意义
分数与除法的关系
分数大小的比较
分数的分类
真分数
假分数
整数
带分数
分数的基本性质
约分
通分
求一个数是另一个数的几分之几
分数和小数的互化
表示把单位“1”平均分成
5
份,取其中
2
份。还表示把2平均分成5份,取其中1份。
表示
2
个
。
表示
2
除以
5
的商。
(分数的意义)
一个物体、一些物体等都可以看作一个整体,把这个整体平均分成若干份,这样的一份或几份都可以用分数来表示。
分数的意义
单位“1”表示:一个物体、一些物体等都可以看作一个整体,一个整体可以用自然数1来表示,通常把它叫做“1”。
分数单位表示:把单位“1”平均分成若干份,表示其中一份的数叫分数单位。
单位“1”与分数单位的区别
1.表示把单位“1”平均分成5份,取其中3份的分数是(
),它的分数单位是(
),再添上(
)个这样的分数单位就是单位“1”。
2.
里面有(
)个
。
(
)里面有3个
。
3个
是(
)。
3.比比两条线段哪个长?
1
3
1
4
分数与除法的关系
工程队修一条5千米长的公路,7天修完,
(1)平均每天修这条公路的(——)千米;
(2)平均每千米要修(——)天;
(3)平均每天修的占这条公路的(——)。
小结:分数与除法的关系
分数可以表示整数除法的商,在表示整数除法时,要用除数作分母,用被除数作分子。
用关系式表示:
被除数÷除数=
————
用字母可以表示成:
a÷b=
——
因为除数不能等于“0”,所以b也不能等于“0”。
被除数
除数
a
b
分数与除法是有区别的。除法是一种运算,它有运算符号,是一个算式;而分数是一个“数”,当它在除法算式中的时候,它可以表示除法算式的结果。
真分数和假分数
意义
特征
真分数
分子比分母小的分数
真分数小于1
假分数
分子比分母大或分子和分母相等的分数
假分数都大于或等于1
4 的分数单位是( ),去掉( )个
这样的分数单位就是最小的合数。
2
7
的分数单位是( ),再添( )
个这样的分数单位就是最小的质数。
7
8
在 中,a是不为0的自然数。
a
5
(真分数?假分数?最小假分数?最大真分数?)
1.分数的基本性质
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
2.约分
把一个分数化成和它相等,但分子、分母都比较小的分数,叫做约分。
3.通分
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
4.最简分数
分子、分母只有公因数1的分数,叫做最简分数。
分数的基本性质
小结:分数的基本性质
约分是分数基本性质中的:分子、分母同时除以相同的数(0除外)的体现。
通分是分数基本性质中的:分子、分母同时乘上相同的数(0除外)的体现。
比较分数的大小除了用同分母、同分子和通分比较方法外,还可以灵活运用其它的方法。
将分数化为最简分数,可以将分子分母分别除以它们的最大公因数,也可以不断地约分,直到分子分母互质为止。
分数
的分子加上8,要使分数
大小不变,分母应该(
)。
0.6=(
)
÷25=
12
(
)
3
5
或3÷5
一个分数的分子扩大20倍,分母缩小20倍,结果如何?
小数化分数,原来有几位小数就在1的后面写几个0做分母,把原来的小数去掉小数点作分子;
化成分数后,能约分的要约分。
分小互化
在(
)里填上合适的分数
50厘米=(
)米
250克=(
)吨
45分=
(
)时
400米=(
)千米
600毫米=(—
)米
40厘米=
(—
)米
15秒=(
—)分
2500平方米=(—
)公顷
50
100
1
2
1
4
3
4
2
5
1
1
4
4
3
2
5
5
同分母分数相加、减,分母不变,只把分子相加减。
1.同分母分数加减法
(1)同分母分数加法的意义及计算方法
(2)同分母分数减法的意义及计算方法
(3)同分母分数连加、连减
异分母分数加减法,先通分,转化为同分母分数进行计算。
2.异分母分数加减法
(1)异分母分数加法
(2)异分母分数减法
(3)分数加减法混合运算
a.不带括号的分数加减法混合运算
b.带括号的分数加减法混合运算
加法的运算定律和减法的性质同样适应于分数中的计算。
1
2
1
4
1
8
1
16
1
32
+
+
+
+
拆项法:
1
2
=
1
-
+
1
2
-
1
4
+
1
4
-
1
8
+
1
8
-
+
1
16
-
1
32
1
16
=
=
1
1
32
-
31
32
在圆圈内填上适当的分数,使每行、每列的三个数加起来的和都等于1。
统计与概率
统计量的复均数、中位数、众数的区别与联系
(一)
平均数:数据之和÷个数
一组数据的平均数只有一个
中位数:
奇数个数据,按大小排序最中间的
一个数据;
偶数个数据,按大小排序最中间的
两个数据的平均数。
一组数据的中位数只有一个
众数:出现次数最多的数据。
一组数据的众数可能有1个或多个(也可能没有)
相同点:
1.都是来描述数据集中趋势的统计量;
2.都可用来反映数据的一般水平;
3.都可用来作为一组数据的代表。
不同点:
(1)平均数是“虚拟数”,
中位数不完全是“虚拟数”;
众数是一组数据中的原数据
,
它是真实存在的。
不同点:
(2)平均数的大小与一组数据里的每个数
据都有关系。
中位数则仅与一组数据的排列位置有
关。
众数的大小只与这组数据中的部分数
据有关,不受极端值的影响。
总复习课件
特殊情况
熟练掌握两种特殊情况。
两数关系
最大公因数
最小公倍数
互质关系
1
两数积
倍数关系
较小数
较大数
求三个数的最小公倍数的特殊规律:
当三个数两两互质时,最小公倍数是这三个数的积;
[2
,7,9]=
126
当三个数都成整倍数关系时,最大的数就是最小公倍数;
[18
,6,54]=
54
当三个数中有两个数成倍数关系时,那么求三个数的最小公倍数就可转化为求这两个数中较大者与第三个数的最小公倍数等。
[18
,6,27]
[18
,27]=108
易混概念对比
1.如果甲数是乙数的5倍,那么,乙数一定
是甲数的倍数。(
)
倍的概念比倍数要广,倍可以适用于小数、
分数和整数,而倍数只适用于整数。
例如:
16是8的2倍,也可以说16是8的倍数。
1.6是0.8的2倍,但是不能说1.6是0.8的倍数。
2.出示判断题:
(1)自然数中,除了奇数就是偶数。(
)
(2)所有的奇数都是质数。
(
)
(3)所有的合数都是偶数。
(
)
(4)自然数中,除了质数就是合数。(
)
(5)质数与质数的积还是质数。
(
)
(6)一个数越大,它的因数的个数就越多。
(
)
注意:奇数里既有质数也有合数还有1。
质数里除了2以外都是奇数。
偶数里除了2以外全是合数。
北京站是104路和103路电车的起发站。104路每3分发一次车,103路每8分发一次车,这两路电车同时发车以后,至少再过多少分又同时发车?
分析:104路电车每3分发一次车,每次发车时间一定是3的倍数,即第二次发车与第一次发车间隔3分,第三次发车与第一次发车间隔6分,而103路电车每8分发一次车,每次发车的时间一定是8的倍数,即第二次发车与第一次发车间隔8分,第三次发车与第一次发车间隔16分,这样就找到了每次两路电车同时发车的时间,就是求3和8的最小公倍数。
小红家的客厅长48分米,宽32分米。现在给客厅的地面铺正方形地砖,有三种砖,你帮小红家想一想,选择哪种地砖能铺得即整齐又不会有余料?
边长3分米
边长6分米
边长8分米
分析:求出48和32的公因数,这个公因数是地砖的边长。
复习长方体和正方体
第一课时
长方形
正方形
三角形
按边分
按角分
等边三角形
等腰三角形
一般三角形
锐角三角形
直角角三角形
钝角三角形
平行四边形
梯形
等腰梯形
直角梯形
一般梯形
组合图形
平面图形
一、建构知识网络
立体图形
正方体
长方体
二、
注重知识的承接,回顾所学平面图形的特征、周长和面积公式。
名称
特征
周长(c)
面积(s)
长方形
两组对边分别平行且相等
(长+宽)×2
C=2(a+b)
长×宽
S=ab
正方形
四边相等
边长×4
C=4a
边长×边长
S=a?
平行四边形
两组对边平行且相等
底×高
S=ah
梯形
只有一组对边平行
(上底+下底)×高÷2
三角形
三条边,三个内角的和等于180°
(底×高)÷2
ah
S=
1
2
(a+b)h
S=
1
2
三、
明确长方体、正方体的异同。
从点、棱、面三方面比较长方体和正方体之间的相同点和不同点
长方体
正方体
相同点
6个面、12条棱、8个顶点
不同点
6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。
6个面都是正方形,
6个面完全相同
相对棱的长度相等
12条棱长度都相等
正方体是特殊的长方体。
用集合图表示:
长方体
正方体
四、
复习长方体、正方体表面积的含义
15
10
8
后
前
上
下
左
右
●
15
10
8
单位:厘米
长方体六个面的面积,就是长方体的表面积。
1.长方体表面积的含义
2.正方体表面积的含义
(1)正方体棱长与每个面边长的关系
后
上
前
下
左
右
正方体展开图的每个面都是正方形,边长就是正方体的棱长,每个面的面积都等于棱长乘棱长。
五、复习长方体、正方体体积公式的推导
长方体的体积
=
长
×
宽
×
高
底面积
正方体的体积
=
棱长
×棱长×棱长
底面积
可看作是高
长方体(或正方体)的
体积
=
底面积
×
高
六、体积与容积区别与联系
异同点
体积
容积
区别
意义不同
物体所占空间的大小,叫做物体的体积。
一个容器所能容纳物体的体积,叫做这个容器的容积。
测量方法不同
从物体外部测量长、宽、高。
从容器里面测量长、宽、高。
单位名称不同
m?、dm?、cm?。
容积单位:L和ml;计量固体时用体积单位。
联系
容积的大小是通过所能容纳物体的体积表示出来的。
计算方法相同
7厘米
5厘米
5厘米
这个长方体的长是(
7
)厘米,宽是(
5
)厘米,高是(
5
)厘米,这个长方体有(
2
)个面是正方形,有(
4
)个面是长方形。
如图
1.
2.
要焊接一个长10cm,宽8cm,高6cm的长方体框架,要准备10cm,宽8cm,高6cm的铁丝各(
4
)根。
3.一个正方体纸盒的棱长是7cm,这个纸盒的棱长总和是(84
)cm。
4.有一根150cm长的铁丝,用这根铁丝焊成了一个正方体的框架,还剩铁丝6cm。这个正方体框架的棱长是(
)厘米。
七、基础知识的练习
150cm
12
8.有一个长方体,底面是一个正方形,高18cm,侧面展开正好是一个正方形。这个长方体的体积是(
)
cm?
。
18÷4=4.5(cm)
4.5×4.5×18
=20.25×18
=364.5(cm?)
18cm
18cm
18cm
10.把棱长是1厘米的小正方体拼摆在一起。如果从右面看,所看到的图形面积是(
)平方厘米,体积是(
)立方厘米。
7
11
11.
一个棱长为2cm的正方体,在它的一个角上挖掉一个棱长为1cm的小正方体,它的表面积是
(???
)cm?。
第二课时:解决相关的实际问题
12cm
15cm
8cm
1.
一条彩带捆扎一种礼盒(如图),如果
接头处的彩带长30cm,求这条彩带的长度。
8×4+12×2+15×2+30=116(cm)
答:这条彩带长116厘米。
2.与右面正方体一致的展开图是(
)。
B
1
2
3
1
2
3
2
3
1
1
2
3
C
B
A
甲
乙
取出石块后
2.1dm
1.8dm
3.
图中有两个完全一样的长方体水箱,水箱的底面积是2平方分米,请结合图中所给信息求出甲箱中石块的体积是多少?
2×(2.1-1.8)=0.6(dm?)
答:石块的体积是0.6dm?。
5厘米
5厘米
5厘米
5.把
积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
(25÷5)×(20÷5)×(20÷5)
=5×4×4
=80(块)
答:纸箱最多可容纳积木80块。
6.把
积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
5厘米
3厘米
3厘米
(25÷3)×(20÷3)×(20÷5)
≈8×6×4
=192(块)
答:纸箱最多可容纳积木192块。
7.一块长方形铁皮,长40cm,宽30cm,像下图这样从4个角各剪掉一个边长为5厘米的正方形,然后做成盒子,这个盒子的容积是多少升?
40cm
30cm
(40-5×2)×(30-5×2)×5=3000(cm?)
3000cm?=3L
答:这个盒子的容积是3升。
12ml=12cm3
24ml=24cm3
一个小球的体积:(24-12)
÷(4-1)=4(cm3)
一个大球的体积:12-4=8(cm3)
左图长、宽、高分别是4cm、3cm、3cm。
它的体积是:
4×3×3=36(cm2)
右图长、宽、高分别是4cm、3cm、4cm。
它的体积是:
4×3×4=48(cm2)
10.用3个长5cm,宽4cm,高3cm的长方体木块,拼成一个表面积最小的长方体。这个长方体的表面积是多少平方厘米?
5cm
4cm
3cm
[5×4+5×(3×3)+4×(3×3)]×2=(20+45+36)×2=202(cm?)
答:这个长方体的表面积是202平方厘米。
3cm
2cm
6cm
6cm
11.有一个形状如图的零件,由一个长方体和一个
正方体组合而成。长方体的长和宽都是6cm,高是3cm,正方体的棱长是2cm。求这个零件的表面积。
2×2×4+6×3×4+6×6×2
=16+72+72
=160(cm?)
答:这个零件的表面积是160平方厘米。
12.由27个棱长为1cm的小正方体组成一个棱长为3cm的大正方体,若自上而下去掉中间的3个小正方体(如图所示),则剩下的几何体的表面积是多少平方厘米?
3×3×6-1×1×2+3×1×4
=54-2+12
=64(cm?)
答:剩下的几何体的表面积是64平方厘米。
13.从一个大长方体上切下一个体积是128立方厘米的小长方体(如图)。原来大长方体的体积是多少立方厘米?
22cm
8cm
切下部分
128÷8×22
=16×22
=352(立方厘米)
答:原来大长方体的体积是352立方厘米。
14.
一个密封的长方体容器里面装有一些水,水深9厘米,如果把这个容器的右面做底,这时容器内的水深多少厘米?
36
10
12
36
10
12
36×10×9=3240(cm3)
3240÷(12×10)=27(cm)
答:容器内的水深27厘米。
分数
分数的意义
分数单位
分子分母的意义
分数与除法的关系
分数大小的比较
分数的分类
真分数
假分数
整数
带分数
分数的基本性质
约分
通分
求一个数是另一个数的几分之几
分数和小数的互化
表示把单位“1”平均分成
5
份,取其中
2
份。还表示把2平均分成5份,取其中1份。
表示
2
个
。
表示
2
除以
5
的商。
(分数的意义)
一个物体、一些物体等都可以看作一个整体,把这个整体平均分成若干份,这样的一份或几份都可以用分数来表示。
分数的意义
单位“1”表示:一个物体、一些物体等都可以看作一个整体,一个整体可以用自然数1来表示,通常把它叫做“1”。
分数单位表示:把单位“1”平均分成若干份,表示其中一份的数叫分数单位。
单位“1”与分数单位的区别
1.表示把单位“1”平均分成5份,取其中3份的分数是(
),它的分数单位是(
),再添上(
)个这样的分数单位就是单位“1”。
2.
里面有(
)个
。
(
)里面有3个
。
3个
是(
)。
3.比比两条线段哪个长?
1
3
1
4
分数与除法的关系
工程队修一条5千米长的公路,7天修完,
(1)平均每天修这条公路的(——)千米;
(2)平均每千米要修(——)天;
(3)平均每天修的占这条公路的(——)。
小结:分数与除法的关系
分数可以表示整数除法的商,在表示整数除法时,要用除数作分母,用被除数作分子。
用关系式表示:
被除数÷除数=
————
用字母可以表示成:
a÷b=
——
因为除数不能等于“0”,所以b也不能等于“0”。
被除数
除数
a
b
分数与除法是有区别的。除法是一种运算,它有运算符号,是一个算式;而分数是一个“数”,当它在除法算式中的时候,它可以表示除法算式的结果。
真分数和假分数
意义
特征
真分数
分子比分母小的分数
真分数小于1
假分数
分子比分母大或分子和分母相等的分数
假分数都大于或等于1
4 的分数单位是( ),去掉( )个
这样的分数单位就是最小的合数。
2
7
的分数单位是( ),再添( )
个这样的分数单位就是最小的质数。
7
8
在 中,a是不为0的自然数。
a
5
(真分数?假分数?最小假分数?最大真分数?)
1.分数的基本性质
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
2.约分
把一个分数化成和它相等,但分子、分母都比较小的分数,叫做约分。
3.通分
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
4.最简分数
分子、分母只有公因数1的分数,叫做最简分数。
分数的基本性质
小结:分数的基本性质
约分是分数基本性质中的:分子、分母同时除以相同的数(0除外)的体现。
通分是分数基本性质中的:分子、分母同时乘上相同的数(0除外)的体现。
比较分数的大小除了用同分母、同分子和通分比较方法外,还可以灵活运用其它的方法。
将分数化为最简分数,可以将分子分母分别除以它们的最大公因数,也可以不断地约分,直到分子分母互质为止。
分数
的分子加上8,要使分数
大小不变,分母应该(
)。
0.6=(
)
÷25=
12
(
)
3
5
或3÷5
一个分数的分子扩大20倍,分母缩小20倍,结果如何?
小数化分数,原来有几位小数就在1的后面写几个0做分母,把原来的小数去掉小数点作分子;
化成分数后,能约分的要约分。
分小互化
在(
)里填上合适的分数
50厘米=(
)米
250克=(
)吨
45分=
(
)时
400米=(
)千米
600毫米=(—
)米
40厘米=
(—
)米
15秒=(
—)分
2500平方米=(—
)公顷
50
100
1
2
1
4
3
4
2
5
1
1
4
4
3
2
5
5
同分母分数相加、减,分母不变,只把分子相加减。
1.同分母分数加减法
(1)同分母分数加法的意义及计算方法
(2)同分母分数减法的意义及计算方法
(3)同分母分数连加、连减
异分母分数加减法,先通分,转化为同分母分数进行计算。
2.异分母分数加减法
(1)异分母分数加法
(2)异分母分数减法
(3)分数加减法混合运算
a.不带括号的分数加减法混合运算
b.带括号的分数加减法混合运算
加法的运算定律和减法的性质同样适应于分数中的计算。
1
2
1
4
1
8
1
16
1
32
+
+
+
+
拆项法:
1
2
=
1
-
+
1
2
-
1
4
+
1
4
-
1
8
+
1
8
-
+
1
16
-
1
32
1
16
=
=
1
1
32
-
31
32
在圆圈内填上适当的分数,使每行、每列的三个数加起来的和都等于1。
统计与概率
统计量的复均数、中位数、众数的区别与联系
(一)
平均数:数据之和÷个数
一组数据的平均数只有一个
中位数:
奇数个数据,按大小排序最中间的
一个数据;
偶数个数据,按大小排序最中间的
两个数据的平均数。
一组数据的中位数只有一个
众数:出现次数最多的数据。
一组数据的众数可能有1个或多个(也可能没有)
相同点:
1.都是来描述数据集中趋势的统计量;
2.都可用来反映数据的一般水平;
3.都可用来作为一组数据的代表。
不同点:
(1)平均数是“虚拟数”,
中位数不完全是“虚拟数”;
众数是一组数据中的原数据
,
它是真实存在的。
不同点:
(2)平均数的大小与一组数据里的每个数
据都有关系。
中位数则仅与一组数据的排列位置有
关。
众数的大小只与这组数据中的部分数
据有关,不受极端值的影响。
