图形的旋转

(共20张PPT)
你有兴趣知道下面的图形是如何生成的吗？
制作者：杨黎英
观看过上面的动画以后，请思考：
　　１哪些部件在运动？
　　２电风扇的风叶绕哪一点转动？
　　３风车的风叶绕哪一点转动？
1.单摆上小球的转动由位置P转到P`，它绕着哪一个点转动？沿着什么方向(顺时针或逆时针)？转动了多少角度？
2.观察了风扇、风车与单摆的运动后，你知道什么是旋转、旋转中心以及旋转角吗？
观察： 单摆的运动
议一议
图形上各点旋转的角度，就是这个图形的旋转角。 　
将一个物体（图形）绕着一个定点沿某一方向转动一个角度，这样的物体（图形）运动称为旋转。
旋转中不动的点叫做旋转中心。
概念
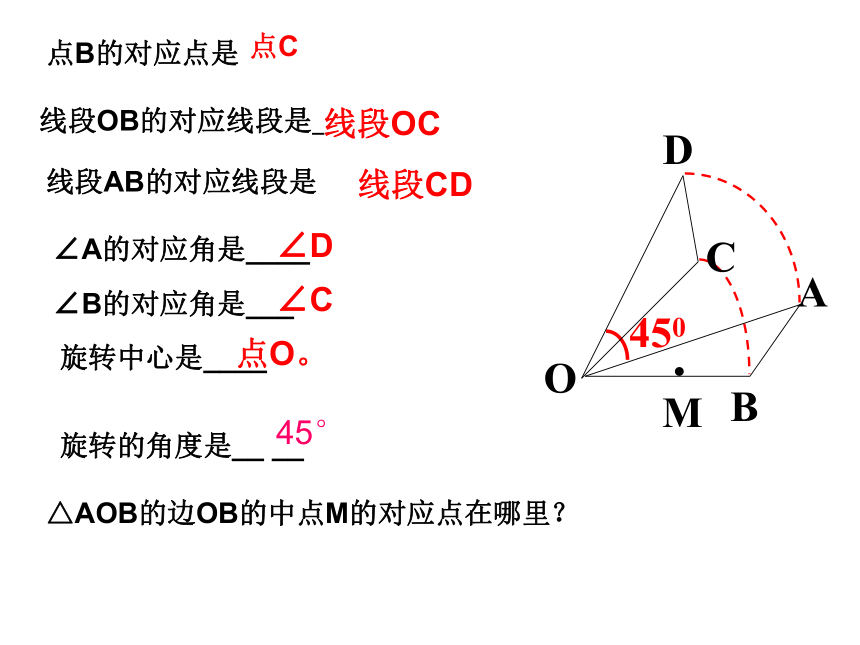
点B的对应点是
线段OB的对应线段是_
线段AB的对应线段是
∠A的对应角是____
∠B的对应角是___
旋转的角度是__ __
△AOB的边OB的中点M的对应点在哪里？
45°
450
D
C
·
M
O
B
A
点C
线段OC
线段CD
∠D
∠C
旋转中心是____
点O。
做一做 ：
如果旋转中心在△ABC的外面点O处，转动60° ，情况将会发生什么变化呢？
　从我们看到的旋转现象以及你所完成的实验中你认为旋转的主要因素是什么？
必须有旋转中心和旋转角
　下面的问题你能回答了吗？
1、 旋转的过程中，旋转中心发生变化了吗？
2、 旋转的过程中，每一点的旋转方向怎样？
3、 旋转的过程中，图形的形状和大小发生变化了吗？
　　
（４）对应点到旋转中心的距离相等．
旋转的基本性质
（１）旋转不改变图形的大小和形状．
（２）图形上的每一点都绕旋转中心沿相同方向转动了相同的角度
（３）任意一对对应点与旋转中心的连线所成的角度都是旋转角．
练兵场：看看你是否真的理解了吗？
例1 如图11.2.6，△ABC是等边三角形，D是BC上一点，△ABD经过旋转后到达△ACE的位置
（1）旋转中心是哪一点？ （2）旋转了多少度？ （3）如果M是AB的中点，那么经过上述旋转后，点M转到了什么位置？ 　　
（3）点M转到了AC 的中点位置上。
解（1）旋转中心是点A。
（2）旋转了60°
例2 如图11.2.7（1），点M是线段AB上一点，将线段AB绕着点M顺时针方向旋转90°，旋转后的线段与原线段的位置有何关系？如果逆时针方向旋转90° 呢？
逆时针方向旋转90° ，A″B″与AB互相垂直。
解：顺时针方向旋转90° ，A′B′与AB互相垂直。
下面的问题一定难不住你。来试试：
1． 如图，△ABC按逆时针方向转动一个角后成为△AB′C′，图中哪一点是旋转中心？请指出一个旋转角。
2． 如图，△ABC与△ADE都是等腰直角三角形，∠C和∠AED都是直角，点E在AB上，如果△ABC经旋转后能与△ADE重合，那么哪一点是旋转中心？旋转了多少度？
　　
练习3：
如图△ABC是等腰直角三角形，D是AB上一点，△CBD经旋转后到达△CAE的位置。
A
E
C
B
D
M
N
(1)旋转中心是:_________;旋转角度是
_________;点B对应点是___________;
点D对应点是_____;线段CB的对应线段
__________;∠B的对应角是____;
(2)如果点M是CB的三分之一点，
那么旋转后点M转到__________
(3)如果连结ED，则△ECD是________ 三角形
点C
90°
点A
点E
线段AC
∠EAC
N点
等腰直角
A
D
C
B
O
2、如图 ABCD，连结AC，将△ ABC旋转到△ CDA的位置，写出旋转中心，旋转角度
3、如图，△ABC、 △CDE为等边三角形，试
画出三角形BCD以点C为中心，顺时针
旋转60°之后的图形
A
B
C
D
E
旋转的性质：﹙1﹚图形上的每一个点都绕旋转中心沿相同方向转动了相同的角度.﹙2﹚任一对应点与旋转中心的连线所成的角都是旋转角且都相等；﹙3﹚对应点到旋转中心的距离相等.
旋转的内涵：图形绕一定点沿顺时针或逆时针方 向转动一定角度
旋转的特征: 旋转不改变图形的大小和形状.改变位置和定向