沪教版(上海)初中数学八年级第一学期 19.2证明举例—证明两条直线垂直 课件(共17张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.2证明举例—证明两条直线垂直 课件(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 435.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览

文档简介
(共17张PPT)
19.2(4)证明举例
——证明两条直线垂直
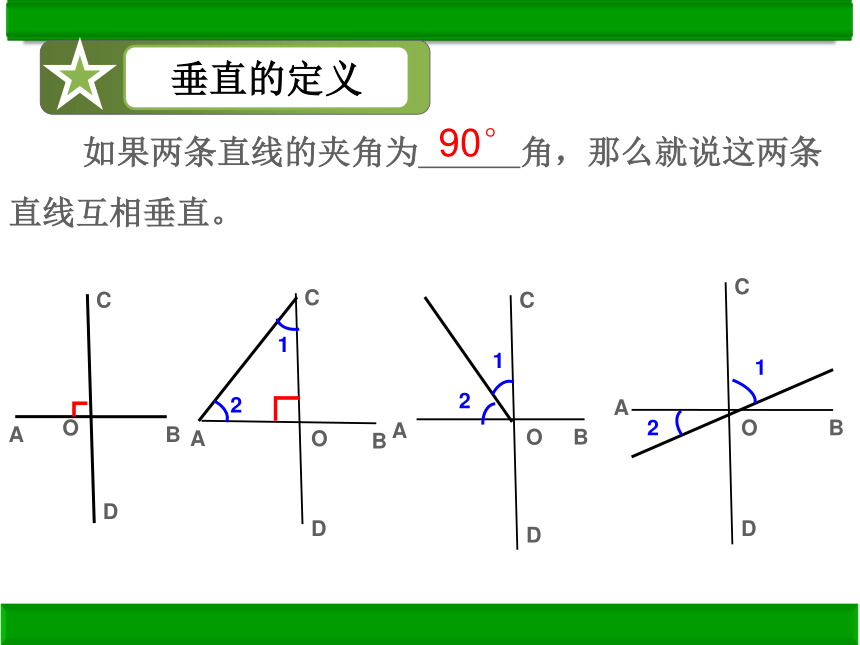
如果两条直线的夹角为??
?
角,那么就说这两条直线互相垂直。
垂直的定义
90°
A
B
C
D
O
A
B
C
D
O
1
2
A
B
C
D
O
1
2
A
B
C
D
O
1
2
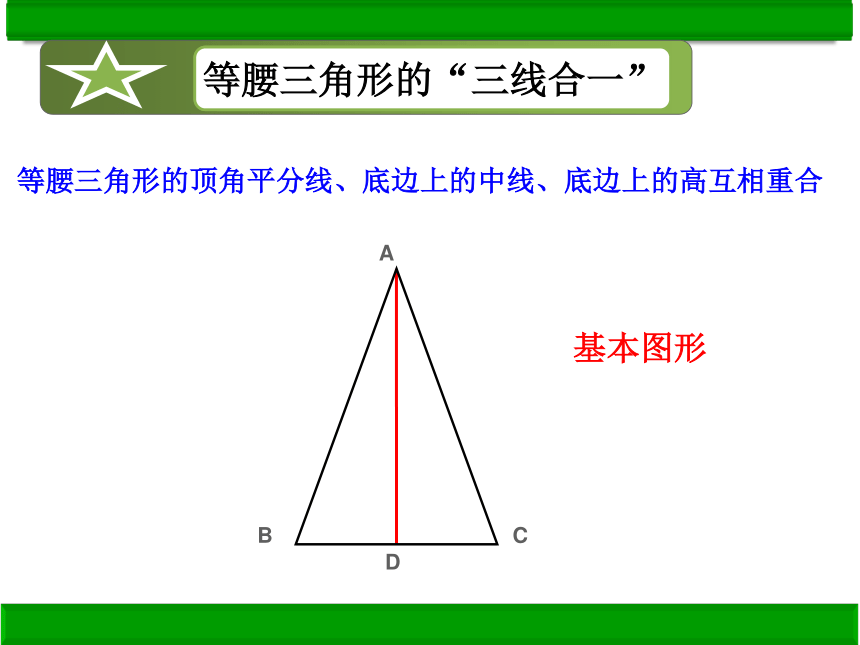
等腰三角形的“三线合一”
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
A
B
C
D
基本图形
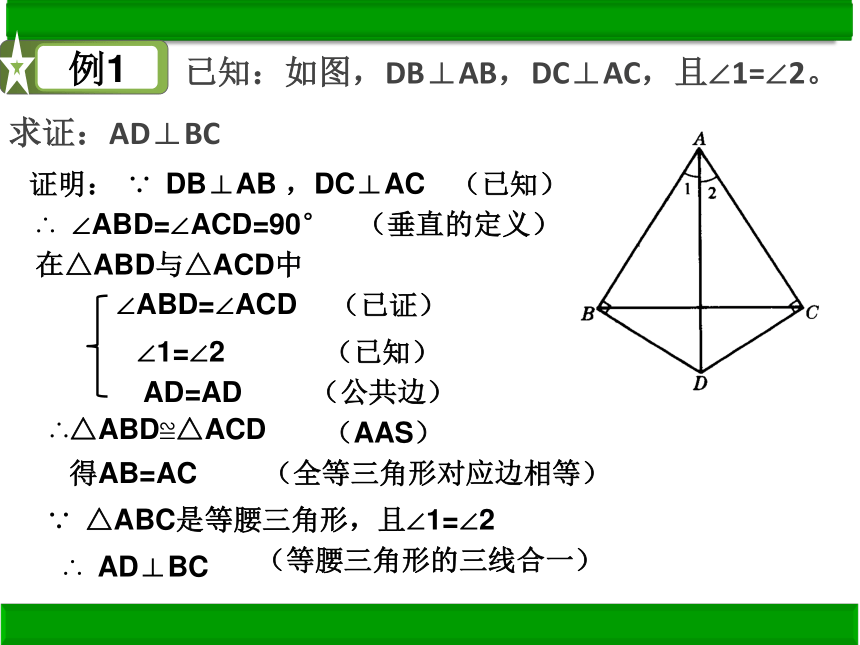
例1
已知:如图,DB⊥AB,DC⊥AC,且∠1=∠2。
求证:AD⊥BC
证明:
∵
DB⊥AB
,DC⊥AC
(已知)
∴
∠ABD=∠ACD=90°
(垂直的定义)
在△ABD与△ACD中
∠1=∠2
AD=AD
∠ABD=∠ACD
(已证)
(已知)
(公共边)
∴△ABD≌△ACD
(AAS)
得AB=AC
(全等三角形对应边相等)
∵
△ABC是等腰三角形,且∠1=∠2
∴
AD⊥BC
(等腰三角形的三线合一)
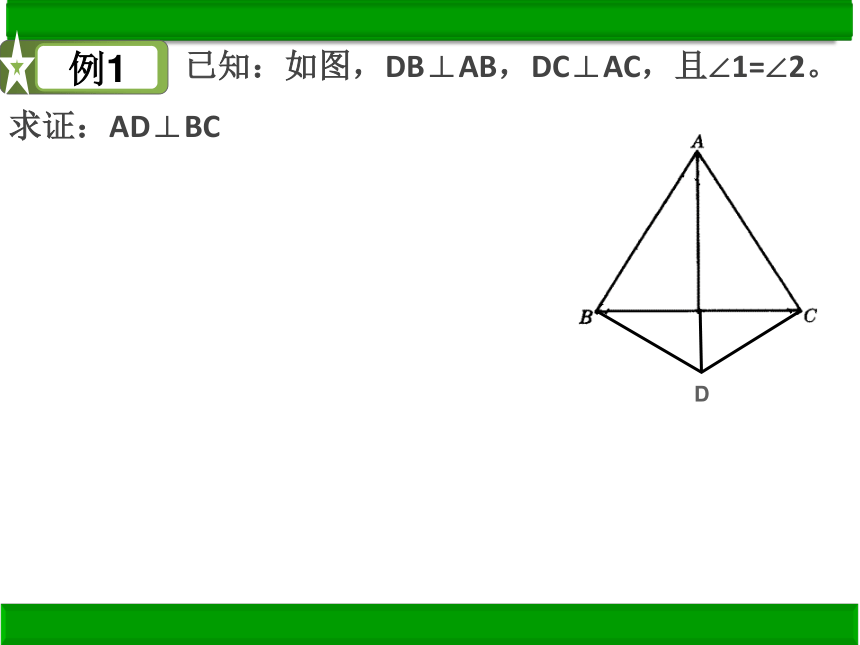
例1
已知:如图,DB⊥AB,DC⊥AC,且∠1=∠2。
求证:AD⊥BC
D
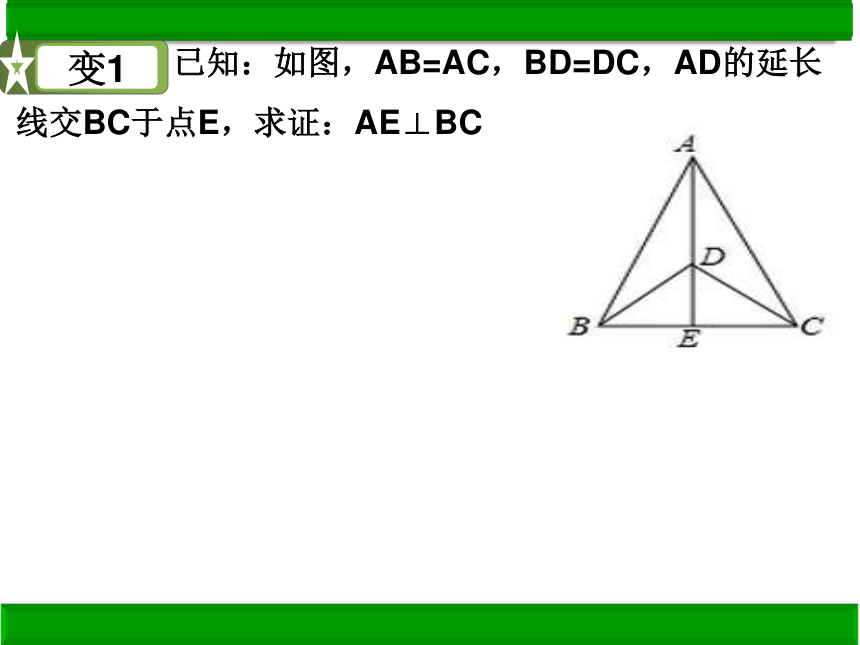
已知:如图,AB=AC,BD=DC,AD的延长线交BC于点E,求证:AE⊥BC
变1
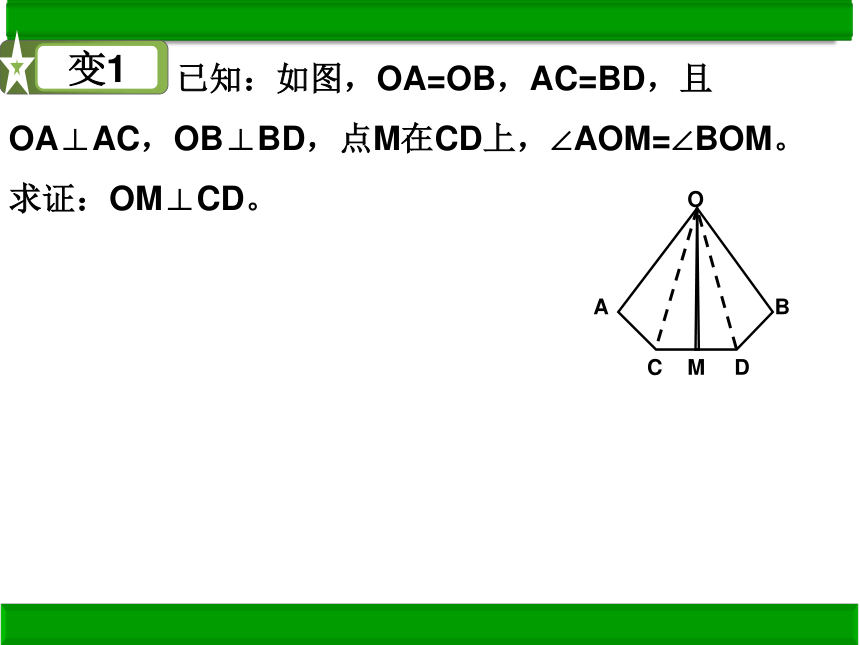
已知:如图,OA=OB,AC=BD,且OA⊥AC,OB⊥BD,点M在CD上,∠AOM=∠BOM。求证:OM⊥CD。
O
A
B
C
D
M
变1
例2
如图:点A、E在CB同侧,且AC⊥CB,EB⊥CB,D为CB上的一点,且AC=BD,CD=BE.
求证:AD⊥DE.
B
A
E
C
D
证明:
∵
AC⊥CB
,EB⊥CB
(已知)
∴
∠ACD=∠EBD=90°
(垂直的定义)
在△ACD与△DBE中
CD=BE
AC=BD
∠ACD=∠EBD
(已知)
(已证)
(已知)
∴△ACD≌△DBE
(SAS)
得∠1=∠2
(全等三角形对应角相等)
∵
∠ADE+∠EDB=∠CAD+∠ACD
∴
AD⊥DE
(垂直定义)
∴∠ADE=90°
(三角形外角性质)
(等式的性质)
1
2
例2
如图:点A、E在CB同侧,且AC⊥CB,EB⊥CB,D为CB上的一点,且AC=BD,CD=BE.
求证:AD⊥DE.
B
E
A
C
D
如图:点A、E在CB同侧,且AC⊥CB,EB⊥CB,D为CB上的一点,且AC=BC,CD=BE.
求证:AD⊥CE.
变1
B
E
A
C
D
O
证明:
∵
AC⊥CB
,EB⊥CB
(已知)
∴
∠ACD=∠EBD=90°
(垂直的定义)
在△ACD与△CBE中
CD=BE
AC=BC
∠ACD=∠EBD
(已知)
(已证)
(已知)
∴△ACD≌△CBE
(SAS)
得∠1=∠2
(全等三角形对应角相等)
1
2
如图:点A、E在CB同侧,且AC⊥CB,EB⊥CB,D为CB上的一点,且AC=BC,CD=BE.
求证:AD⊥CE.
变1
B
E
A
C
D
如图,△ABC是等腰直角三角形,∠ACB=90°,E是AC上一点,延长BC到D,使CD=CE,联结BE,AD。试判断BE与AD有什么关系,并证明。
变2
B
A
E
C
D
F
BE和AD的数量关系是:
BE=AD
BE和AD的位置关系是:
BE⊥AD
如图,在△ABC中,AD=BD=CD,求证:AC⊥BC
C
A
B
D
变3
如果三角形一边上的中线等于这边的一半,
那么这个三角形是
直角三角形
证明:
∵
AD=BD=CD
(已知)
∴
∠DAC=∠DCA
(等边对等角)
∠DCB=∠DBC
∵∠DAC+∠DCA+∠DCB+∠DBC=180°
(三角形内角和性质)
∴2∠DCA+2∠DCB=180°
(等量代换)
∴∠DCA+∠DCB=90°
(等式的性质)
即∠ACB=90°
∴
AC⊥BC
(垂直的定义)
已知:如图,以锐角△ABC的边AB、AC为直角边作等腰直角△ABD和等腰直角△ACE,CD与BE交于点F。试判断CD与BE的关系
拓展题
已知:如图,以锐角△ABC的边AB、AC为直角边作等腰直角△ABD和等腰直角△ACE,CD与BE交于点F。试判断CD与BE的关系
拓展题
A
B
C
D
E
[知识要点]
证明两条直线垂直的基本方法:
(1)转化为证两条直线的夹角等于90°。
(2)利用等腰三角形的“三线合一”的性质证。
[方法要点]
1、从复杂的图形背景中分离出基本图形,使问题简单化。
2、添置辅助线将图形“补形”或连结构造等腰三角形,突显基本图形。
课堂小结
布置作业
1、练习册19.2(4)
2、学案19.2(4)
19.2(4)证明举例
——证明两条直线垂直
如果两条直线的夹角为??
?
角,那么就说这两条直线互相垂直。
垂直的定义
90°
A
B
C
D
O
A
B
C
D
O
1
2
A
B
C
D
O
1
2
A
B
C
D
O
1
2
等腰三角形的“三线合一”
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
A
B
C
D
基本图形
例1
已知:如图,DB⊥AB,DC⊥AC,且∠1=∠2。
求证:AD⊥BC
证明:
∵
DB⊥AB
,DC⊥AC
(已知)
∴
∠ABD=∠ACD=90°
(垂直的定义)
在△ABD与△ACD中
∠1=∠2
AD=AD
∠ABD=∠ACD
(已证)
(已知)
(公共边)
∴△ABD≌△ACD
(AAS)
得AB=AC
(全等三角形对应边相等)
∵
△ABC是等腰三角形,且∠1=∠2
∴
AD⊥BC
(等腰三角形的三线合一)
例1
已知:如图,DB⊥AB,DC⊥AC,且∠1=∠2。
求证:AD⊥BC
D
已知:如图,AB=AC,BD=DC,AD的延长线交BC于点E,求证:AE⊥BC
变1
已知:如图,OA=OB,AC=BD,且OA⊥AC,OB⊥BD,点M在CD上,∠AOM=∠BOM。求证:OM⊥CD。
O
A
B
C
D
M
变1
例2
如图:点A、E在CB同侧,且AC⊥CB,EB⊥CB,D为CB上的一点,且AC=BD,CD=BE.
求证:AD⊥DE.
B
A
E
C
D
证明:
∵
AC⊥CB
,EB⊥CB
(已知)
∴
∠ACD=∠EBD=90°
(垂直的定义)
在△ACD与△DBE中
CD=BE
AC=BD
∠ACD=∠EBD
(已知)
(已证)
(已知)
∴△ACD≌△DBE
(SAS)
得∠1=∠2
(全等三角形对应角相等)
∵
∠ADE+∠EDB=∠CAD+∠ACD
∴
AD⊥DE
(垂直定义)
∴∠ADE=90°
(三角形外角性质)
(等式的性质)
1
2
例2
如图:点A、E在CB同侧,且AC⊥CB,EB⊥CB,D为CB上的一点,且AC=BD,CD=BE.
求证:AD⊥DE.
B
E
A
C
D
如图:点A、E在CB同侧,且AC⊥CB,EB⊥CB,D为CB上的一点,且AC=BC,CD=BE.
求证:AD⊥CE.
变1
B
E
A
C
D
O
证明:
∵
AC⊥CB
,EB⊥CB
(已知)
∴
∠ACD=∠EBD=90°
(垂直的定义)
在△ACD与△CBE中
CD=BE
AC=BC
∠ACD=∠EBD
(已知)
(已证)
(已知)
∴△ACD≌△CBE
(SAS)
得∠1=∠2
(全等三角形对应角相等)
1
2
如图:点A、E在CB同侧,且AC⊥CB,EB⊥CB,D为CB上的一点,且AC=BC,CD=BE.
求证:AD⊥CE.
变1
B
E
A
C
D
如图,△ABC是等腰直角三角形,∠ACB=90°,E是AC上一点,延长BC到D,使CD=CE,联结BE,AD。试判断BE与AD有什么关系,并证明。
变2
B
A
E
C
D
F
BE和AD的数量关系是:
BE=AD
BE和AD的位置关系是:
BE⊥AD
如图,在△ABC中,AD=BD=CD,求证:AC⊥BC
C
A
B
D
变3
如果三角形一边上的中线等于这边的一半,
那么这个三角形是
直角三角形
证明:
∵
AD=BD=CD
(已知)
∴
∠DAC=∠DCA
(等边对等角)
∠DCB=∠DBC
∵∠DAC+∠DCA+∠DCB+∠DBC=180°
(三角形内角和性质)
∴2∠DCA+2∠DCB=180°
(等量代换)
∴∠DCA+∠DCB=90°
(等式的性质)
即∠ACB=90°
∴
AC⊥BC
(垂直的定义)
已知:如图,以锐角△ABC的边AB、AC为直角边作等腰直角△ABD和等腰直角△ACE,CD与BE交于点F。试判断CD与BE的关系
拓展题
已知:如图,以锐角△ABC的边AB、AC为直角边作等腰直角△ABD和等腰直角△ACE,CD与BE交于点F。试判断CD与BE的关系
拓展题
A
B
C
D
E
[知识要点]
证明两条直线垂直的基本方法:
(1)转化为证两条直线的夹角等于90°。
(2)利用等腰三角形的“三线合一”的性质证。
[方法要点]
1、从复杂的图形背景中分离出基本图形,使问题简单化。
2、添置辅助线将图形“补形”或连结构造等腰三角形,突显基本图形。
课堂小结
布置作业
1、练习册19.2(4)
2、学案19.2(4)
