七年级数学乘方
图片预览








文档简介
(共23张PPT)
咸安区汀泗中学 陈 平
义务教育课程标准实验教科书 七年级 上册
珠穆朗玛峰是世界的最高峰,它
的海拔高度是8844.43米.
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰.
你信吗?
如果这张长方形的纸面积为1,如此折叠五次后所得长方形面积是多少?
把一张长方形的纸对折后,再对折,如此操作五次后共有多少层?
折纸游戏
2×2 ×2 ×2 ×2
2×2 ×2 ×2 ×2
下列两个算式有什么共同特征?
共同点:求几个相同因数的积的运算.
n 个a 相加
a+a+a+…+a=
多个相同因数相乘,有没有一种简便的式子表达呢?
a n
·
正方形面积公式:a ×a = a2
25
(-3)4
(-3)×(-3)×(-3)×(-3)应记作_______;
a7
猜想: a×a ×… ×a ×a 的结果记作什么?
n个
正方体体积公式: a×a ×a = a3
类比:
2×2 ×2 ×2×2 应记作______;
应记作______ ;
a×a ×a ×a×a×a×a 应记作______.
一般地,n个相同因数a 相乘,即
读作:a的n次方
求n个相同因数积的运算,叫做乘方.
也可读作:a的n次幂
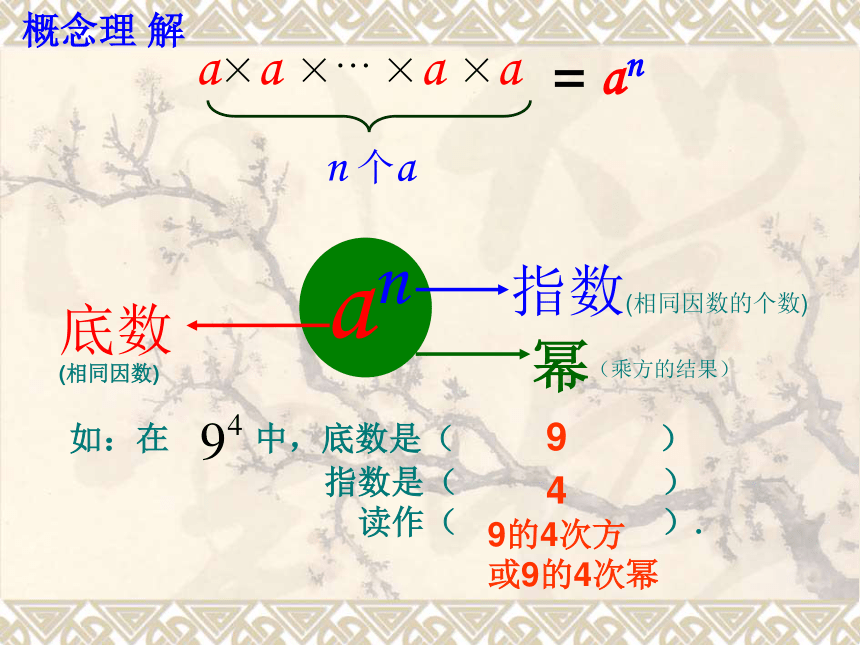
定义:
记作:
乘方的结果叫做幂.
an
底数(相同因数)
指数(相同因数的个数)
幂
a×a ×… ×a ×a
n 个a
= an
如:在 中,底数是( )
指数是( )
读作( ).
9
4
9的4次方
或9的4次幂
概念理 解
(乘方的结果)
25
2的五次方或2的五次幂
(-3)4
-3的四次方或-3的四次幂
(-3)×(-3)×(-3)×(-3)应记作______, 读作:______________________;
a7
a 的7次方或a 的7次幂
2×2 ×2 ×2×2应记作_____, 读作:____________________;
应记作 ______,读作:__________________________;
注意:一个数可以看作这个数本身的一次方.
的五次方或 的五次幂
a×a ×a ×a×a×a×a 应记作_____,读作:____________________.
⑴
⑵
你发现当底数为分数和负数的时候应注意什么?
[加括号]
计算:
3. ①
2.
3. ① 03 ② 010
解:
03=0
010=0.
① ② ③ ④
1. ①22 ② 23
2. ①
③
④
②
②
1. ①
②
乘方运算的符号法则:
正数的任何次幂都是正数;
负数的偶次幂是正数,奇次幂是负数;
0的任何正整数次幂都是0.
归纳
回顾
在有理数的乘法中,我们学习了“几个不是0的数相乘:
负因数个数是偶数时,积为正数;
负因数个数是奇数时,积为负数”.
1. 判断下列各题是否正确.
① 33=3 ×3
② 2+2+2=23
③ 23=2×2 ×2
×
×
√
( )
×
④
⑤
-24=(-2)×(-2)×(-2)×(-2) ( )
×
( )
( )
( )
⑤ ⑥ ⑦ ⑧
① ② ③ ④
你能说出盾牌后面男,女同学各是哪几个吗?
3.填空
(1) -2的平方是___,-2的立方是___;
(2) 平方得9的数是______;
(3) 立方得-27的数是____;
(4) _____ 的平方等于它本身;
(5) 如果 =16, 那么n =____.
4
-8
-3
0和1
3和-3
4
0.1毫米×230
一张厚度是0.1毫米的纸,将它连续对折30 次后,厚度为:
12个珠穆朗玛峰的高度:
8844.43米 ×12=106133.16米.
这下你该相信了吧!
=0.1毫米×1073742418
=107374.1824米
显示
按键
1073742418 .
30.
2.
2.
2
30
=
这节课你有哪些收获
2.选做题:棋盘上的学问.
1 .必做题:课本第47页习题1.5第一题.
古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
咸安区汀泗中学 陈 平
义务教育课程标准实验教科书 七年级 上册
珠穆朗玛峰是世界的最高峰,它
的海拔高度是8844.43米.
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰.
你信吗?
如果这张长方形的纸面积为1,如此折叠五次后所得长方形面积是多少?
把一张长方形的纸对折后,再对折,如此操作五次后共有多少层?
折纸游戏
2×2 ×2 ×2 ×2
2×2 ×2 ×2 ×2
下列两个算式有什么共同特征?
共同点:求几个相同因数的积的运算.
n 个a 相加
a+a+a+…+a=
多个相同因数相乘,有没有一种简便的式子表达呢?
a n
·
正方形面积公式:a ×a = a2
25
(-3)4
(-3)×(-3)×(-3)×(-3)应记作_______;
a7
猜想: a×a ×… ×a ×a 的结果记作什么?
n个
正方体体积公式: a×a ×a = a3
类比:
2×2 ×2 ×2×2 应记作______;
应记作______ ;
a×a ×a ×a×a×a×a 应记作______.
一般地,n个相同因数a 相乘,即
读作:a的n次方
求n个相同因数积的运算,叫做乘方.
也可读作:a的n次幂
定义:
记作:
乘方的结果叫做幂.
an
底数(相同因数)
指数(相同因数的个数)
幂
a×a ×… ×a ×a
n 个a
= an
如:在 中,底数是( )
指数是( )
读作( ).
9
4
9的4次方
或9的4次幂
概念理 解
(乘方的结果)
25
2的五次方或2的五次幂
(-3)4
-3的四次方或-3的四次幂
(-3)×(-3)×(-3)×(-3)应记作______, 读作:______________________;
a7
a 的7次方或a 的7次幂
2×2 ×2 ×2×2应记作_____, 读作:____________________;
应记作 ______,读作:__________________________;
注意:一个数可以看作这个数本身的一次方.
的五次方或 的五次幂
a×a ×a ×a×a×a×a 应记作_____,读作:____________________.
⑴
⑵
你发现当底数为分数和负数的时候应注意什么?
[加括号]
计算:
3. ①
2.
3. ① 03 ② 010
解:
03=0
010=0.
① ② ③ ④
1. ①22 ② 23
2. ①
③
④
②
②
1. ①
②
乘方运算的符号法则:
正数的任何次幂都是正数;
负数的偶次幂是正数,奇次幂是负数;
0的任何正整数次幂都是0.
归纳
回顾
在有理数的乘法中,我们学习了“几个不是0的数相乘:
负因数个数是偶数时,积为正数;
负因数个数是奇数时,积为负数”.
1. 判断下列各题是否正确.
① 33=3 ×3
② 2+2+2=23
③ 23=2×2 ×2
×
×
√
( )
×
④
⑤
-24=(-2)×(-2)×(-2)×(-2) ( )
×
( )
( )
( )
⑤ ⑥ ⑦ ⑧
① ② ③ ④
你能说出盾牌后面男,女同学各是哪几个吗?
3.填空
(1) -2的平方是___,-2的立方是___;
(2) 平方得9的数是______;
(3) 立方得-27的数是____;
(4) _____ 的平方等于它本身;
(5) 如果 =16, 那么n =____.
4
-8
-3
0和1
3和-3
4
0.1毫米×230
一张厚度是0.1毫米的纸,将它连续对折30 次后,厚度为:
12个珠穆朗玛峰的高度:
8844.43米 ×12=106133.16米.
这下你该相信了吧!
=0.1毫米×1073742418
=107374.1824米
显示
按键
1073742418 .
30.
2.
2.
2
30
=
这节课你有哪些收获
2.选做题:棋盘上的学问.
1 .必做题:课本第47页习题1.5第一题.
古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
