(人教新课标)四年级数学上册学案 垂直与平行
文档属性
| 名称 | (人教新课标)四年级数学上册学案 垂直与平行 |

|
|
| 格式 | doc | ||
| 文件大小 | 56.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-16 00:00:00 | ||
图片预览


文档简介
垂直与平行
刘德武
一、复习
1.师:我们研究了四年数学了,你觉得数学与什么有关系?
生:数 图形
师:所有的数学知识无外乎两大类——数和形
问:猜,平行与垂直主要跟数有关系还是跟形有关系?
师:形就是图形,包括四个方面:点、线、面、体
点 几个例子,角的顶点,线段射线的端点
线 有直线、射线
面 有平面图形、长方形、正方形等
体 正方体、长方体
问:今天我们研究的是有关形的数学问题,大家想可能是哪些关系?
生:可能是两个点、两条线、两个面、两个体的关系。
师:我们今天研究的是两条直线的位置关系。——垂直与平行
2.怎样的两条直线互相平行呢?
请同学们拿出圆形纸片,用尺子画两条直线,要求这两条直线互相平行?你怎么理解怎么画?
再在另一张圆形纸片上,用尺子画两条互相垂直
3.学生操作画在圆形纸片上。
二、研究平行与垂直
1.展示学生的作品
(1)师:我们一起来欣赏同学们的作品。
(2)互相交叉的情况在数学上叫相交。相交中有一个角度比较特殊的。
(3)什么样的两条直线叫互相平行?
生:不交叉的
什么样的两条直线叫互相垂直?
生:
问:只要交叉的就垂直吗?
生:不是,必须相交成直角。
问:互相垂直必须满足几个条件
生:两个:相交、成直角。
(4)书上是怎么说的?(屏幕)
*一个平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行。
*如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
教师解释为什么叫垂足。(幻灯片)
(5)问:我们看看字典上是怎样解释的平行和垂直。(幻灯片)
【垂直】几何学生指两条直线、两个平面或一条直线和一个平面相交成直角。
【平行】两个平面或在同一个平面内的两条直线永远不相交:~~线、~~面。
师演示两个本子:两个平面互相平行,这是一个平面,这也是一个平面,(高架路)
“同一个平面内”:大屏幕是一个平面,我们把圆形纸片方在桌面上,也是同一个平面。
问:在同一个平面内,两条直线永远也不相交,不相交就行了,永远是什么意思?
生:无限延伸。
师:向左延伸,或者向右延伸,无论多长也不相交。
三、练习
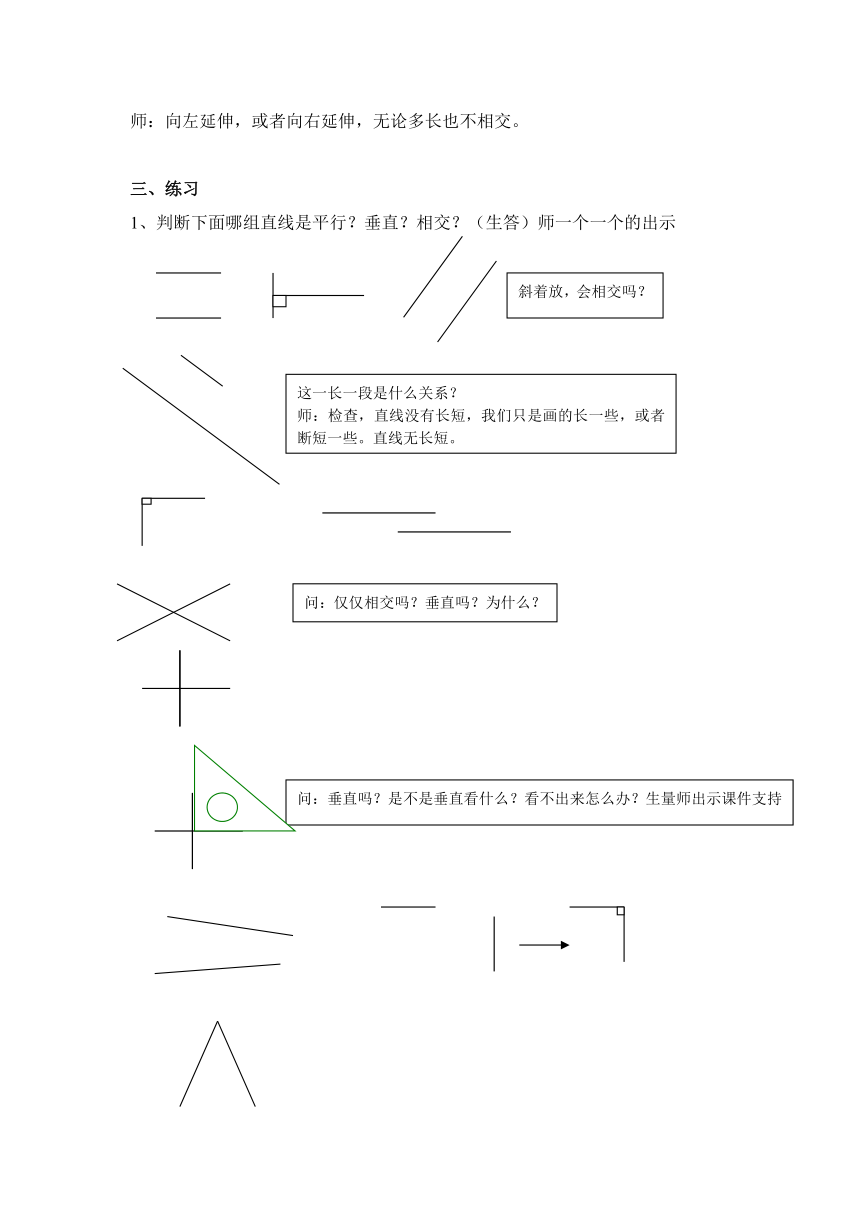
1、判断下面哪组直线是平行?垂直?相交?(生答)师一个一个的出示
2.我们的数学课上和作业本中有没有平行和垂直的关系呢?
+ × = ≈ 曲线(在同一平面内,永远也不相交,是平行线吗?为什么?曲线) > <
作业本中的
3.在图形中认识相交和平行。
我们以前研究的图形中有相交和平行的关系吗?(逐个变形)
长方形中谁与谁互相平行?谁与谁互相垂直?
谁与谁平行?几组对边互相平行?(上下一组,左右一组)
两组对边分别平行。
梯形中,谁与谁互相平行?
平行吗?垂直吗?相交吗?任何两条边相交。
正六边形
六个角相等,六条边也相等。谁与谁平行 用一句话怎么说?对边平行,3组对边分别平行。
四、研究三者之间的关系
1.教师用铅笔演示、假设这是两条直线,学生判断
。。。。。。
问:哪一种最特殊?是相交吗?特殊的名字(垂直)
2.平行、相交、垂直三者到底是怎样的关系呢?
(1)我用3个图表示出了他们三者的关系,生判断。
哪个对?为什么?
生:第一个对。因为平行就一定不相交。相交中有垂直。
(2)
判断:
①两条直线相交,那么一定互相垂直。( )
②两条直线垂直,那么一定互相相交。( )
③两条直线平行,那么一定互不相交。( )
④在同一平面内,有3条直线abc,彼此不重合,(重合是一条直线)
已知a与b平行,b与c平行,那么,a与c( )
出图:
已知a与b垂直,b与c垂直,那么,a与c( )。
学生比划
已知a与b相交,b与c相交,那么,a与c( )。
五、生活中的平行与垂直现象。(幻灯片)
1.看图片,楼梯中的平行与垂直。
2.学生举例:生活中、教室里的平行与垂直。
3,生活中有时要避免相交(高架桥图)
六、干扰现象。(幻灯片)
1.出示多个相交的线,找交点。
2.加上一组平行线,问:黄线是什么关系?(视觉冲突)
反复出现,发现一会直一回弯,干扰现象。
七、在“垂直”中找垂足(幻灯片)
四个直角,结果垂足?一个公共点
垂(10个)直(12个)
斜着放,会相交吗?
这一长一段是什么关系?
师:检查,直线没有长短,我们只是画的长一些,或者断短一些。直线无长短。
问:仅仅相交吗?垂直吗?为什么?
问:垂直吗?是不是垂直看什么?看不出来怎么办?生量师出示课件支持
对号,两条直线 刚巧是直角呢? 一条曲线 两条曲线构成,
相交吗?为什么? 是相交的关系吗?
这是相交中最特殊的情况。
2次出现垂直。
相交
垂直
平行
平行
相交
垂直
平行
垂直
相交
平行
相交
垂直
a
b
c
a
b
a
b
c
刘德武
一、复习
1.师:我们研究了四年数学了,你觉得数学与什么有关系?
生:数 图形
师:所有的数学知识无外乎两大类——数和形
问:猜,平行与垂直主要跟数有关系还是跟形有关系?
师:形就是图形,包括四个方面:点、线、面、体
点 几个例子,角的顶点,线段射线的端点
线 有直线、射线
面 有平面图形、长方形、正方形等
体 正方体、长方体
问:今天我们研究的是有关形的数学问题,大家想可能是哪些关系?
生:可能是两个点、两条线、两个面、两个体的关系。
师:我们今天研究的是两条直线的位置关系。——垂直与平行
2.怎样的两条直线互相平行呢?
请同学们拿出圆形纸片,用尺子画两条直线,要求这两条直线互相平行?你怎么理解怎么画?
再在另一张圆形纸片上,用尺子画两条互相垂直
3.学生操作画在圆形纸片上。
二、研究平行与垂直
1.展示学生的作品
(1)师:我们一起来欣赏同学们的作品。
(2)互相交叉的情况在数学上叫相交。相交中有一个角度比较特殊的。
(3)什么样的两条直线叫互相平行?
生:不交叉的
什么样的两条直线叫互相垂直?
生:
问:只要交叉的就垂直吗?
生:不是,必须相交成直角。
问:互相垂直必须满足几个条件
生:两个:相交、成直角。
(4)书上是怎么说的?(屏幕)
*一个平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行。
*如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
教师解释为什么叫垂足。(幻灯片)
(5)问:我们看看字典上是怎样解释的平行和垂直。(幻灯片)
【垂直】几何学生指两条直线、两个平面或一条直线和一个平面相交成直角。
【平行】两个平面或在同一个平面内的两条直线永远不相交:~~线、~~面。
师演示两个本子:两个平面互相平行,这是一个平面,这也是一个平面,(高架路)
“同一个平面内”:大屏幕是一个平面,我们把圆形纸片方在桌面上,也是同一个平面。
问:在同一个平面内,两条直线永远也不相交,不相交就行了,永远是什么意思?
生:无限延伸。
师:向左延伸,或者向右延伸,无论多长也不相交。
三、练习
1、判断下面哪组直线是平行?垂直?相交?(生答)师一个一个的出示
2.我们的数学课上和作业本中有没有平行和垂直的关系呢?
+ × = ≈ 曲线(在同一平面内,永远也不相交,是平行线吗?为什么?曲线) > <
作业本中的
3.在图形中认识相交和平行。
我们以前研究的图形中有相交和平行的关系吗?(逐个变形)
长方形中谁与谁互相平行?谁与谁互相垂直?
谁与谁平行?几组对边互相平行?(上下一组,左右一组)
两组对边分别平行。
梯形中,谁与谁互相平行?
平行吗?垂直吗?相交吗?任何两条边相交。
正六边形
六个角相等,六条边也相等。谁与谁平行 用一句话怎么说?对边平行,3组对边分别平行。
四、研究三者之间的关系
1.教师用铅笔演示、假设这是两条直线,学生判断
。。。。。。
问:哪一种最特殊?是相交吗?特殊的名字(垂直)
2.平行、相交、垂直三者到底是怎样的关系呢?
(1)我用3个图表示出了他们三者的关系,生判断。
哪个对?为什么?
生:第一个对。因为平行就一定不相交。相交中有垂直。
(2)
判断:
①两条直线相交,那么一定互相垂直。( )
②两条直线垂直,那么一定互相相交。( )
③两条直线平行,那么一定互不相交。( )
④在同一平面内,有3条直线abc,彼此不重合,(重合是一条直线)
已知a与b平行,b与c平行,那么,a与c( )
出图:
已知a与b垂直,b与c垂直,那么,a与c( )。
学生比划
已知a与b相交,b与c相交,那么,a与c( )。
五、生活中的平行与垂直现象。(幻灯片)
1.看图片,楼梯中的平行与垂直。
2.学生举例:生活中、教室里的平行与垂直。
3,生活中有时要避免相交(高架桥图)
六、干扰现象。(幻灯片)
1.出示多个相交的线,找交点。
2.加上一组平行线,问:黄线是什么关系?(视觉冲突)
反复出现,发现一会直一回弯,干扰现象。
七、在“垂直”中找垂足(幻灯片)
四个直角,结果垂足?一个公共点
垂(10个)直(12个)
斜着放,会相交吗?
这一长一段是什么关系?
师:检查,直线没有长短,我们只是画的长一些,或者断短一些。直线无长短。
问:仅仅相交吗?垂直吗?为什么?
问:垂直吗?是不是垂直看什么?看不出来怎么办?生量师出示课件支持
对号,两条直线 刚巧是直角呢? 一条曲线 两条曲线构成,
相交吗?为什么? 是相交的关系吗?
这是相交中最特殊的情况。
2次出现垂直。
相交
垂直
平行
平行
相交
垂直
平行
垂直
相交
平行
相交
垂直
a
b
c
a
b
a
b
c
