沪科版数学九年级上册21.5 第1课时 反比例函数教学课件(30张PPT)
文档属性
| 名称 | 沪科版数学九年级上册21.5 第1课时 反比例函数教学课件(30张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 898.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 22:23:44 | ||
图片预览










文档简介
(共30张PPT)
第21章
二次函数与反比例函数
沪科版数学九年级上册
21.5
反比例函数
第1课时
反比例函数
1.
理解并掌握反比例函数的概念.
(重点)
2.
从实际问题中抽象出反比例函数的概念,能根据已知
条件确定反比例函数的解析式.
(重点、难点)
学习目标
本节目标
?
?
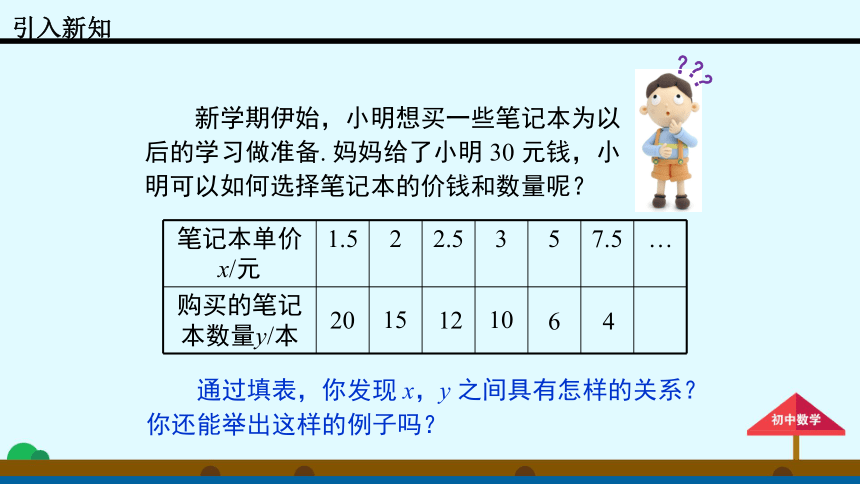
新学期伊始,小明想买一些笔记本为以后的学习做准备.
妈妈给了小明
30
元钱,小明可以如何选择笔记本的价钱和数量呢?
笔记本单价x/元
1.5
2
2.5
3
5
7.5
…
购买的笔记本数量y/本
通过填表,你发现
x,y
之间具有怎样的关系?你还能举出这样的例子吗?
20
15
12
10
6
4
?
引入新知
下列问题中,变量间具有函数关系吗?如果有,请写出它们的解析式.
合作探究
(1)
京沪线铁路全程为1463
km,某次列车的平均速
度v
(单位:km/h)
随此次列车的全程运行时间
t
(单位:h)
的变化而变化;
反比例函数的概念
新知讲解
(2)
某住宅小区要种植一块面积为
1000
m2
的矩形草
坪,草坪的长
y
(单位:m)
随宽
x
(单位:m)的
变化而变化;
(3)
已知北京市的总面积为1.68×104
km2
,人均占
有面积
S
(km2/人)
随全市总人口
n
(单位:人)
的
变化而变化.
观察以上三个解析式,你觉得它们有什么共同特点?
问题:
都具有
的形式,其中
是常数.
分式
分子
(k为常数,k
≠
0)
的函数,
叫做反比例函数,其中
x
是自变量,y
是函数.
一般地,形如
反比例函数
(k≠0)
的自变量
x
的取值范围是什么?
思考:
因为
x
作为分母,不能等于零,因此自变量
x
的取值范围是所有非零实数.
但实际问题中,应根据具体情况来确定反比例函数自变量的取值范围.
例如,在前面得到的第一个解析式
中,t
的取值范围是
t>0,且当
t
取每一个确定的
值时,v
都有唯一确定的值与其对应.
反比例函数除了可以用
(k
≠
0)
的形式表示,还有没有其他表达方式?
想一想:
反比例函数的三种表达方式:(注意
k
≠
0)
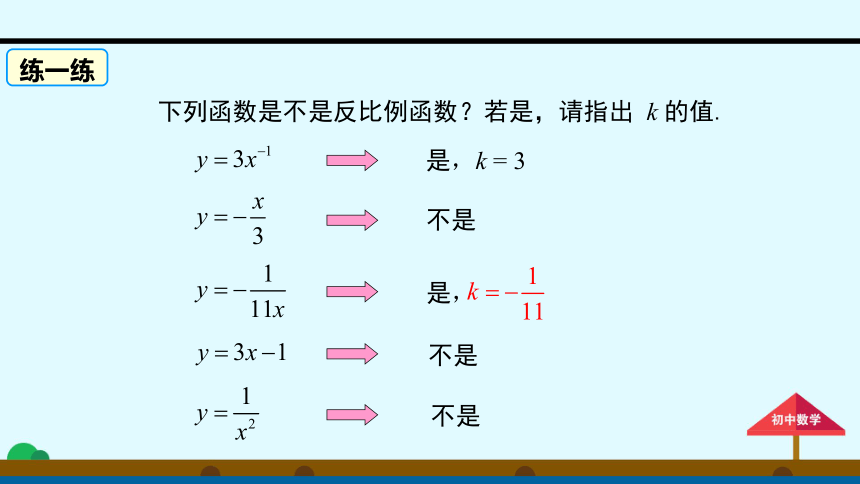
下列函数是不是反比例函数?若是,请指出
k
的值.
是,k
=
3
不是
不是
不是
练一练
是,
解:因为
是反比例函数
所以
4-k2=0,
k-2≠0.
解得
k
=-2.
所以该反比例函数的解析式为
方法总结:已知某个函数为反比例函数,只需要根据反比例函数的定义列出方程(组)求解即可.
例1
若函数
是反比例函数,求
k的值,并写出该反比例函数的解析式.
1.
已知函数
是反比例函数,则
k
必须满足
.
2.
当m=
时,
是反比例函数.
k≠2
且
k≠-1
±1
练一练
例2
已知
y
是
x
的反比例函数,并且当
x=2时,y=6.
(1)
写出
y
关于
x
的函数解析式;
提示:因为
y
是
x
的反比例函数,所以设
.把
x=2
和
y=6
代入上式,就可求出常数
k
的值.
解:设
.
因为当
x=2时,y=6,所以有
解得
k
=12.
因此
确定反比例函数的解析式
(2)
当
x=4
时,求
y
的值.
解:把
x=4
代入
,得
方法总结:用待定系数法求反比例函数解析式的一般步骤:①设出含有待定系数的反比例函数解析式,
②将已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程;③解方程,求出待定系数;
④写出反比例函数解析式.
练一练
已知变量
y
与
x
成反比例,且当
x=3时,y=-4.
(1)
写出
y
关于
x
的函数解析式;
(2)
当
y=6
时,求
x
的值.
解:(1)
设
.
因为当
x=3时,y=-4,所以有
解得
k
=-12.
因此
(2)
把
y=6
代入
,得
解得
x
=-2.
例3:在压力不变的情况下,某物体承受的压强p
Pa是它的受力面积S
m2的反比例函数,如图.
(1)求p与S之间的函数表达式;
(2)当S=0.5时,求p的值.
解:(1)设
(k≠0),
因为函数图象过点(0.1,1000),
代入上式,得
解得k=100.
所以p与S的函数表达式是
;
(2)当S=0.5时,
p
s
O
0.1
1000
例4
人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体是动态的,车速增加,视野变窄.
当车速为
50km/h
时,视野为
80
度,如果视野
f
(度)
是车速
v
(km/h)
的反比例函数,求
f
关于
v
的函数解析式,并计算当车速为100km/h
时视野的度数.
建立简单的反比例函数模型
当
v=100
时,f
=40.
所以当车速为100km/h
时视野为40度.
解:设
.
由题意知,当
v
=50时,f
=80,所以
解得
k
=4000.
因此
如图所示,已知菱形
ABCD
的面积为180,设它的两条对角线
AC,BD的长分别为x,y.
写出变量
y与
x
之间的关系式,并指出它是什么函数.
A
B
C
D
练一练
解:因为菱形的面积等于两条对角线长
乘积的一半,
所以
所以变量
y与
x
之间的关系式为
,
它是反比例函数.
1.
生活中有许多反比例函数的例子,在下面的实例中,
x
和
y
成反比例函数关系的有
(
)
①
x人共饮水10
kg,平均每人饮水
y
kg;②底面半径为
x
m,高为
y
m的圆柱形水桶的体积为10
m3;③用铁丝做一个圆,铁丝的长为
x
cm,做成圆的半径为
y
cm;④在水龙头前放满一桶水,出水的速度为
x,放满一桶水的时间
y
A.
1个
B.
2个
C.
3个
D.
4个
B
巩固练习
A.
B.
C.
D.
2.
下列函数中,y是x的反比例函数的是
(
)
A
3.
填空
(1)
若
是反比例函数,则
m
的取值范围
是
.
(2)
若
是反比例函数,则m的取值范
围是
.
(3)
若
是反比例函数,则m的取值范围
是
.
m
≠
1
m
≠
0
且
m
≠
-2
m
=
-1
4.
已知
y
与
x+1
成反比例,并且当
x
=
3
时,y
=
4.
(1)
写出
y
关于
x
的函数解析式;
(2)
当
x
=
7
时,求
y
的值.
解:(1)
设
,因为当
x
=
3
时,y
=4
,
所以有
,解得
k
=16,因此
.
(2)
当
x
=
7
时,
5.
小明家离学校
1000
m,每天他往返于两地之间,有
时步行,有时骑车.假设小明每天上学时的平均速
度为
v
(
m/min
),所用的时间为
t
(
min
).
(1)
求变量
v
和
t
之间的函数关系式;
解:
(t>0).
(2)
小明星期二步行上学用了
25
min,星期三骑自行
车上学用了
8
min,那么他星期三上学时的平均
速度比星期二快多少?
125-40=85
(
m/min
).
答:他星期三上学时的平均速度比星期二快
85
m/min.
解:当
t=25
时,
;
当
t=8
时,
.
能力提升:
6.
已知
y
=
y1+y2,y1与
(x-1)
成正比例,y2
与
(x
+
1)
成反比例,当
x
=
0
时,y
=-3;当
x
=1
时,y
=
-1,
求:
(1)
y
关于
x
的关系式;
解:设
y1
=
k1(x-1)
(k1≠0),
(k2≠0),
则
.
∵
x
=
0
时,y
=-3;x
=1
时,y
=
-1,
-3=-k1+k2
,
∴k1=1,k2=-2.
∴
∴
(2)
当
x
=
时,y
的值.
解:把
x
=
代入
(1)
中函数关系式,得
y
=
建立反比例函数模型
用待定系数法求反比例函数解析式
反比例函数:定义/三种表达方式
反比例函数
本节小结
第21章
二次函数与反比例函数
沪科版数学九年级上册
第21章
二次函数与反比例函数
沪科版数学九年级上册
21.5
反比例函数
第1课时
反比例函数
1.
理解并掌握反比例函数的概念.
(重点)
2.
从实际问题中抽象出反比例函数的概念,能根据已知
条件确定反比例函数的解析式.
(重点、难点)
学习目标
本节目标
?
?
新学期伊始,小明想买一些笔记本为以后的学习做准备.
妈妈给了小明
30
元钱,小明可以如何选择笔记本的价钱和数量呢?
笔记本单价x/元
1.5
2
2.5
3
5
7.5
…
购买的笔记本数量y/本
通过填表,你发现
x,y
之间具有怎样的关系?你还能举出这样的例子吗?
20
15
12
10
6
4
?
引入新知
下列问题中,变量间具有函数关系吗?如果有,请写出它们的解析式.
合作探究
(1)
京沪线铁路全程为1463
km,某次列车的平均速
度v
(单位:km/h)
随此次列车的全程运行时间
t
(单位:h)
的变化而变化;
反比例函数的概念
新知讲解
(2)
某住宅小区要种植一块面积为
1000
m2
的矩形草
坪,草坪的长
y
(单位:m)
随宽
x
(单位:m)的
变化而变化;
(3)
已知北京市的总面积为1.68×104
km2
,人均占
有面积
S
(km2/人)
随全市总人口
n
(单位:人)
的
变化而变化.
观察以上三个解析式,你觉得它们有什么共同特点?
问题:
都具有
的形式,其中
是常数.
分式
分子
(k为常数,k
≠
0)
的函数,
叫做反比例函数,其中
x
是自变量,y
是函数.
一般地,形如
反比例函数
(k≠0)
的自变量
x
的取值范围是什么?
思考:
因为
x
作为分母,不能等于零,因此自变量
x
的取值范围是所有非零实数.
但实际问题中,应根据具体情况来确定反比例函数自变量的取值范围.
例如,在前面得到的第一个解析式
中,t
的取值范围是
t>0,且当
t
取每一个确定的
值时,v
都有唯一确定的值与其对应.
反比例函数除了可以用
(k
≠
0)
的形式表示,还有没有其他表达方式?
想一想:
反比例函数的三种表达方式:(注意
k
≠
0)
下列函数是不是反比例函数?若是,请指出
k
的值.
是,k
=
3
不是
不是
不是
练一练
是,
解:因为
是反比例函数
所以
4-k2=0,
k-2≠0.
解得
k
=-2.
所以该反比例函数的解析式为
方法总结:已知某个函数为反比例函数,只需要根据反比例函数的定义列出方程(组)求解即可.
例1
若函数
是反比例函数,求
k的值,并写出该反比例函数的解析式.
1.
已知函数
是反比例函数,则
k
必须满足
.
2.
当m=
时,
是反比例函数.
k≠2
且
k≠-1
±1
练一练
例2
已知
y
是
x
的反比例函数,并且当
x=2时,y=6.
(1)
写出
y
关于
x
的函数解析式;
提示:因为
y
是
x
的反比例函数,所以设
.把
x=2
和
y=6
代入上式,就可求出常数
k
的值.
解:设
.
因为当
x=2时,y=6,所以有
解得
k
=12.
因此
确定反比例函数的解析式
(2)
当
x=4
时,求
y
的值.
解:把
x=4
代入
,得
方法总结:用待定系数法求反比例函数解析式的一般步骤:①设出含有待定系数的反比例函数解析式,
②将已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程;③解方程,求出待定系数;
④写出反比例函数解析式.
练一练
已知变量
y
与
x
成反比例,且当
x=3时,y=-4.
(1)
写出
y
关于
x
的函数解析式;
(2)
当
y=6
时,求
x
的值.
解:(1)
设
.
因为当
x=3时,y=-4,所以有
解得
k
=-12.
因此
(2)
把
y=6
代入
,得
解得
x
=-2.
例3:在压力不变的情况下,某物体承受的压强p
Pa是它的受力面积S
m2的反比例函数,如图.
(1)求p与S之间的函数表达式;
(2)当S=0.5时,求p的值.
解:(1)设
(k≠0),
因为函数图象过点(0.1,1000),
代入上式,得
解得k=100.
所以p与S的函数表达式是
;
(2)当S=0.5时,
p
s
O
0.1
1000
例4
人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体是动态的,车速增加,视野变窄.
当车速为
50km/h
时,视野为
80
度,如果视野
f
(度)
是车速
v
(km/h)
的反比例函数,求
f
关于
v
的函数解析式,并计算当车速为100km/h
时视野的度数.
建立简单的反比例函数模型
当
v=100
时,f
=40.
所以当车速为100km/h
时视野为40度.
解:设
.
由题意知,当
v
=50时,f
=80,所以
解得
k
=4000.
因此
如图所示,已知菱形
ABCD
的面积为180,设它的两条对角线
AC,BD的长分别为x,y.
写出变量
y与
x
之间的关系式,并指出它是什么函数.
A
B
C
D
练一练
解:因为菱形的面积等于两条对角线长
乘积的一半,
所以
所以变量
y与
x
之间的关系式为
,
它是反比例函数.
1.
生活中有许多反比例函数的例子,在下面的实例中,
x
和
y
成反比例函数关系的有
(
)
①
x人共饮水10
kg,平均每人饮水
y
kg;②底面半径为
x
m,高为
y
m的圆柱形水桶的体积为10
m3;③用铁丝做一个圆,铁丝的长为
x
cm,做成圆的半径为
y
cm;④在水龙头前放满一桶水,出水的速度为
x,放满一桶水的时间
y
A.
1个
B.
2个
C.
3个
D.
4个
B
巩固练习
A.
B.
C.
D.
2.
下列函数中,y是x的反比例函数的是
(
)
A
3.
填空
(1)
若
是反比例函数,则
m
的取值范围
是
.
(2)
若
是反比例函数,则m的取值范
围是
.
(3)
若
是反比例函数,则m的取值范围
是
.
m
≠
1
m
≠
0
且
m
≠
-2
m
=
-1
4.
已知
y
与
x+1
成反比例,并且当
x
=
3
时,y
=
4.
(1)
写出
y
关于
x
的函数解析式;
(2)
当
x
=
7
时,求
y
的值.
解:(1)
设
,因为当
x
=
3
时,y
=4
,
所以有
,解得
k
=16,因此
.
(2)
当
x
=
7
时,
5.
小明家离学校
1000
m,每天他往返于两地之间,有
时步行,有时骑车.假设小明每天上学时的平均速
度为
v
(
m/min
),所用的时间为
t
(
min
).
(1)
求变量
v
和
t
之间的函数关系式;
解:
(t>0).
(2)
小明星期二步行上学用了
25
min,星期三骑自行
车上学用了
8
min,那么他星期三上学时的平均
速度比星期二快多少?
125-40=85
(
m/min
).
答:他星期三上学时的平均速度比星期二快
85
m/min.
解:当
t=25
时,
;
当
t=8
时,
.
能力提升:
6.
已知
y
=
y1+y2,y1与
(x-1)
成正比例,y2
与
(x
+
1)
成反比例,当
x
=
0
时,y
=-3;当
x
=1
时,y
=
-1,
求:
(1)
y
关于
x
的关系式;
解:设
y1
=
k1(x-1)
(k1≠0),
(k2≠0),
则
.
∵
x
=
0
时,y
=-3;x
=1
时,y
=
-1,
-3=-k1+k2
,
∴k1=1,k2=-2.
∴
∴
(2)
当
x
=
时,y
的值.
解:把
x
=
代入
(1)
中函数关系式,得
y
=
建立反比例函数模型
用待定系数法求反比例函数解析式
反比例函数:定义/三种表达方式
反比例函数
本节小结
第21章
二次函数与反比例函数
沪科版数学九年级上册
