九年级一对一--直线和圆的位置关系(3)
文档属性
| 名称 | 九年级一对一--直线和圆的位置关系(3) |

|
|
| 格式 | zip | ||
| 文件大小 | 35.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-16 00:00:00 | ||
图片预览

文档简介
姓名 年级 九 性别 总课时____第___课
教学目标 知识点:考点:能力:方法:
难点重点
课堂教学过程 课前检查 作业完成情况:优□ 良□ 中□ 差□ 建议__________________________________________
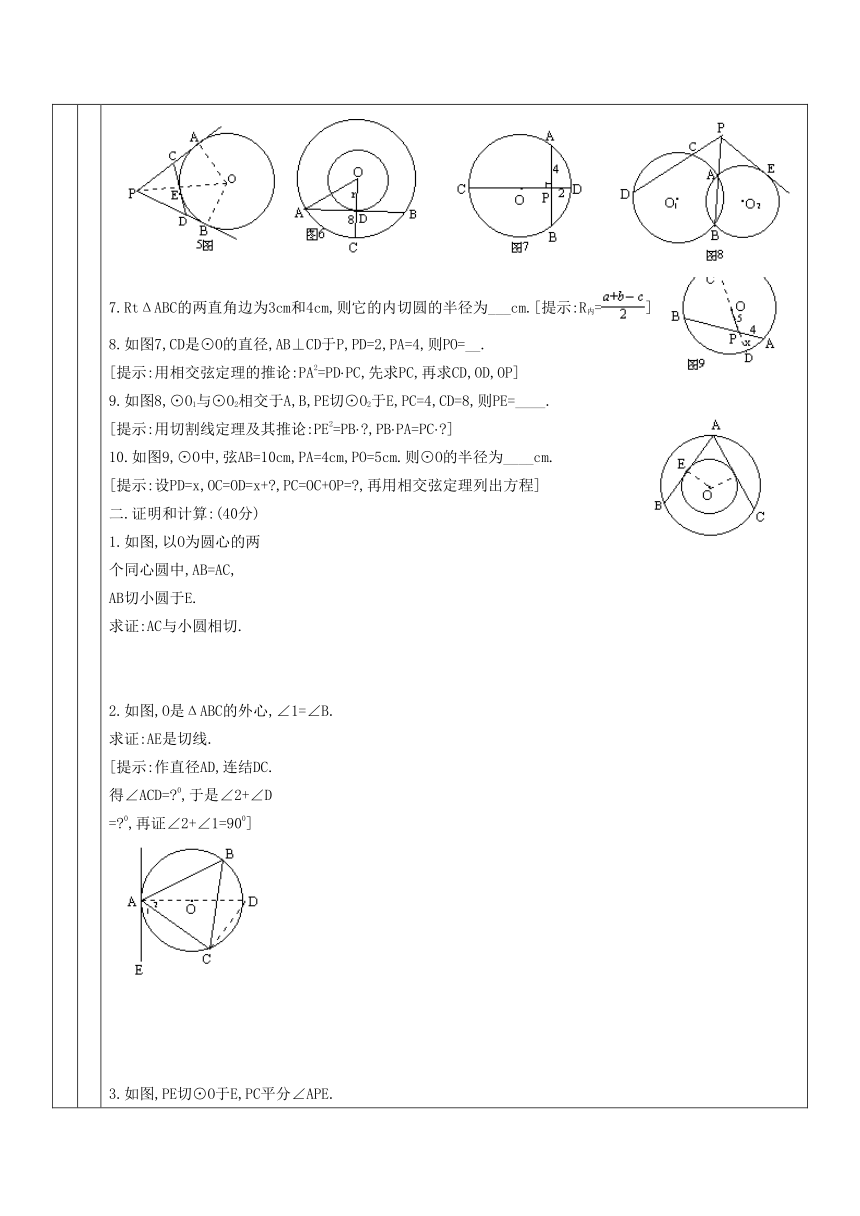
过程 直线与圆的位置关系(3)一.填空:(每空5分,共60分) 1.如图1,O是ΔABC的外心,I是ΔABC的内心,∠C=800,则∠AOB=____度,∠AIB=_____度. [提示:内心是Δ内角平分线的交点;外心是Δ外接圆的圆心,也是三边中垂线的交点]2.如图2,PA,PB切⊙O于A,B,点C在上,∠P=500,则∠C=____.[提示:作辅助线如图.切线⊥过切点的半径.四边形PAOB的内角和为3600.可先求∠AOB和∠D,再求∠C]3.如图3,⊙O是ΔABC的内切圆,切点为D,E,F.AB=10,BC=9,AC=7.则AD=_____. [提示:设AD=x,由切线长定理得:AD=AF=x,BE=BD= -x,CE=CF= -x.根据BE+EC=BC=9列出方程]4.如图4,PA切⊙O于A,∠PAC=500,则∠AOC=______,∠B=____. [提示:作辅助线如图.弦切角等于它所夹弧对的圆周角.可先求∠D]5.如图5,PA,PB,CD切⊙O于A,B,E.⊙O的半径为5cm,∠APB=600.则PA=____cm,ΔPCD的周长为_____cm. [提示:先证CE=CA,DE=DB,可得:PC+PD+CE+DE=PC+PD+CA+DB=PA+ ]6.如图6,两个同心圆中,大圆的弦AB切小圆于D,AB=24cm,CD=8cm,则小圆的半径为_____cm. [提示:设小圆半径为r,则OA=OC= r+ ,先求AD,再用勾股定理列方程]7.RtΔABC的两直角边为3cm和4cm,则它的内切圆的半径为___cm.[提示:R内= ]8.如图7,CD是⊙O的直径,AB⊥CD于P,PD=2,PA=4,则PO=__. [提示:用相交弦定理的推论:PA2=PD ·PC,先求PC,再求CD,OD,OP]9.如图8,⊙O1与⊙O2相交于A,B,PE切⊙O2于E,PC=4, CD=8,则PE=____.[提示:用切割线定理及其推论: PE2=PB· ,PB ·PA=PC· ]10.如图9,⊙O中, 弦AB=10cm,PA=4cm,PO=5cm.则⊙O的半径为____cm. [提示:设PD=x,OC=OD=x+ ,PC=OC+OP= ,再用相交弦定理列出方程]二.证明和计算:(40分)1.如图,以O为圆心的两个同心圆中,AB=AC,AB切小圆于E.求证:AC与小圆相切. 2.如图,O是ΔABC的外心, ∠1=∠B.求证:AE是切线. [提示:作直径AD,连结DC. 得∠ACD= 0,于是∠2+∠D = 0,再证∠2+∠1=900] 3.如图,PE切⊙O于E,PC平分∠APE. 求证:EC=ED. [提示:用Δ外角定理: ∠1=∠ +∠ ,∠2=∠ +∠ .弦切角∠5=∠ ]4.如图,EB切⊙O于B, =. 求证:AB2=CA· AE. [提示:由= ∠ =∠ BC∥AD ∠2=∠ ] 5.如图,AB是⊙O的直 径,AB⊥CD,PE切⊙O于E.求证: PF2=PC ·PD. [先证PF=PE.∠1+∠B= 0,∠A+∠B= 0,弦切角∠2=∠ ]附加题:(10分)如图,DF切圆于D,∠1=∠2.求证:(1)AC∥DF.(2)AF 2=AE ·DF. [提示:先证AF ·FC=AE ·DF]————教学具体内容要有提示或附后
课堂检测 听课及知识掌握情况反馈_________________________________________________________。测试题(累计不超过20分钟)_______道;成绩_______;教学需:加快□;保持□;放慢□;增加内容□
课后巩固 作业_____题; 巩固复习____________________ ; 预习布置_____________________
签字 教学组长签字: 学习管理师:
老师课后赏识评价 老师最欣赏的地方:
老师想知道的事情:
老师的建议:
教学目标 知识点:考点:能力:方法:
难点重点
课堂教学过程 课前检查 作业完成情况:优□ 良□ 中□ 差□ 建议__________________________________________
过程 直线与圆的位置关系(3)一.填空:(每空5分,共60分) 1.如图1,O是ΔABC的外心,I是ΔABC的内心,∠C=800,则∠AOB=____度,∠AIB=_____度. [提示:内心是Δ内角平分线的交点;外心是Δ外接圆的圆心,也是三边中垂线的交点]2.如图2,PA,PB切⊙O于A,B,点C在上,∠P=500,则∠C=____.[提示:作辅助线如图.切线⊥过切点的半径.四边形PAOB的内角和为3600.可先求∠AOB和∠D,再求∠C]3.如图3,⊙O是ΔABC的内切圆,切点为D,E,F.AB=10,BC=9,AC=7.则AD=_____. [提示:设AD=x,由切线长定理得:AD=AF=x,BE=BD= -x,CE=CF= -x.根据BE+EC=BC=9列出方程]4.如图4,PA切⊙O于A,∠PAC=500,则∠AOC=______,∠B=____. [提示:作辅助线如图.弦切角等于它所夹弧对的圆周角.可先求∠D]5.如图5,PA,PB,CD切⊙O于A,B,E.⊙O的半径为5cm,∠APB=600.则PA=____cm,ΔPCD的周长为_____cm. [提示:先证CE=CA,DE=DB,可得:PC+PD+CE+DE=PC+PD+CA+DB=PA+ ]6.如图6,两个同心圆中,大圆的弦AB切小圆于D,AB=24cm,CD=8cm,则小圆的半径为_____cm. [提示:设小圆半径为r,则OA=OC= r+ ,先求AD,再用勾股定理列方程]7.RtΔABC的两直角边为3cm和4cm,则它的内切圆的半径为___cm.[提示:R内= ]8.如图7,CD是⊙O的直径,AB⊥CD于P,PD=2,PA=4,则PO=__. [提示:用相交弦定理的推论:PA2=PD ·PC,先求PC,再求CD,OD,OP]9.如图8,⊙O1与⊙O2相交于A,B,PE切⊙O2于E,PC=4, CD=8,则PE=____.[提示:用切割线定理及其推论: PE2=PB· ,PB ·PA=PC· ]10.如图9,⊙O中, 弦AB=10cm,PA=4cm,PO=5cm.则⊙O的半径为____cm. [提示:设PD=x,OC=OD=x+ ,PC=OC+OP= ,再用相交弦定理列出方程]二.证明和计算:(40分)1.如图,以O为圆心的两个同心圆中,AB=AC,AB切小圆于E.求证:AC与小圆相切. 2.如图,O是ΔABC的外心, ∠1=∠B.求证:AE是切线. [提示:作直径AD,连结DC. 得∠ACD= 0,于是∠2+∠D = 0,再证∠2+∠1=900] 3.如图,PE切⊙O于E,PC平分∠APE. 求证:EC=ED. [提示:用Δ外角定理: ∠1=∠ +∠ ,∠2=∠ +∠ .弦切角∠5=∠ ]4.如图,EB切⊙O于B, =. 求证:AB2=CA· AE. [提示:由= ∠ =∠ BC∥AD ∠2=∠ ] 5.如图,AB是⊙O的直 径,AB⊥CD,PE切⊙O于E.求证: PF2=PC ·PD. [先证PF=PE.∠1+∠B= 0,∠A+∠B= 0,弦切角∠2=∠ ]附加题:(10分)如图,DF切圆于D,∠1=∠2.求证:(1)AC∥DF.(2)AF 2=AE ·DF. [提示:先证AF ·FC=AE ·DF]————教学具体内容要有提示或附后
课堂检测 听课及知识掌握情况反馈_________________________________________________________。测试题(累计不超过20分钟)_______道;成绩_______;教学需:加快□;保持□;放慢□;增加内容□
课后巩固 作业_____题; 巩固复习____________________ ; 预习布置_____________________
签字 教学组长签字: 学习管理师:
老师课后赏识评价 老师最欣赏的地方:
老师想知道的事情:
老师的建议:
同课章节目录
