九年级一对一--直线和圆的位置关系(1)
文档属性
| 名称 | 九年级一对一--直线和圆的位置关系(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 18.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-16 00:00:00 | ||
图片预览


文档简介
姓名 年级 九 性别 总课时____第___课
教学目标 知识点:直线与圆相切的判定考点:直线与圆相切的应用能力:方法:
难点重点 直线与圆相切的判定 切线长定理、
课堂教学过程 课前检查 作业完成情况:优□ 良□ 中□ 差□ 建议__________________________________________
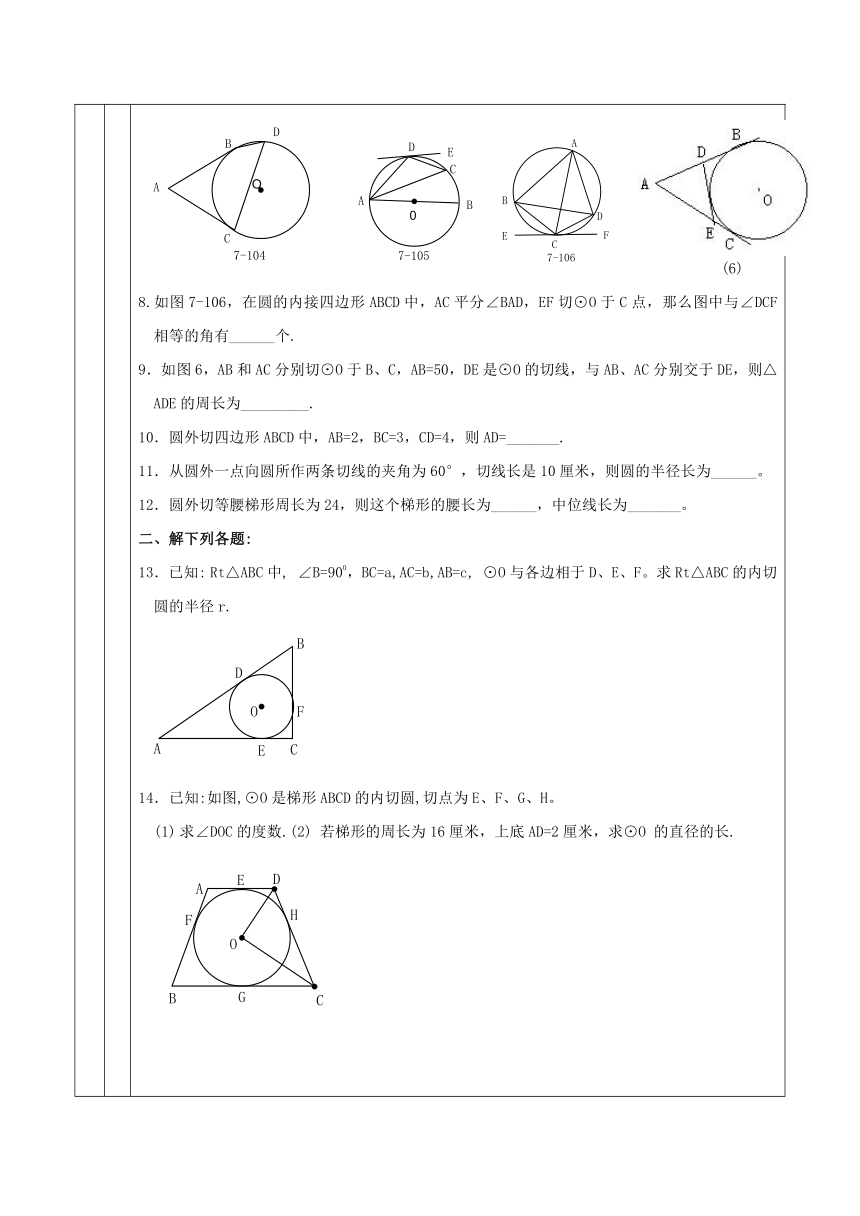
过程 直线和圆的位置关系(A)一、填空:1.如图1,AB、CD相交于P,PA>PB,AB=12cm,P将CD分成4cm和5cm两部分, 那么PA=____cm.2.如图2,PC为⊙O的切线,C为切点,PAB为⊙O的割线,若PA=4cm,AB=5cm,那么PC=_____cm. (1) (2) (3) (4) (5)3.如图3,⊙O的半径为3cm,OP=6cm,PC、PD切⊙O于C、D, 那么∠CPD=_____,PC=____cm..4.如图4, D为弦AB的中点,CD⊥AB于D,AB=10cm、CD=3cm,那么⊙O的半径为____cm。5.如图5,Rt△ABC中,∠ACB=90°,AC=5,BC=12,以C为圆心,CA为半径做⊙C,交AB于D,交BC于E。那么AD=_______。6.如图7-104,AB、AC是⊙O的两条切线,切点为B、C,D是优弧上一点,已知∠BAC=80°,那么∠BDC= 度.7.如图7-105,AB是⊙O的直径,C、D是⊙O上的点,∠BAC=20°,=,DE是⊙O的切线,则∠EDC= . (6)8.如图7-106,在圆的内接四边形ABCD中,AC平分∠BAD,EF切⊙O于C点,那么图中与∠DCF相等的角有______个.9.如图6,AB和AC分别切⊙O于B、C,AB=50,DE是⊙O的切线,与AB、AC分别交于DE,则△ADE的周长为_________.10.圆外切四边形ABCD中,AB=2,BC=3,CD=4,则AD=_______.11.从圆外一点向圆所作两条切线的夹角为60°,切线长是10厘米,则圆的半径长为______。12.圆外切等腰梯形周长为24,则这个梯形的腰长为______,中位线长为_______。二、解下列各题:13.已知: Rt△ABC中, ∠B=900,BC=a,AC=b,AB=c, ⊙O与各边相于D、E、F。求Rt△ABC的内切圆的半径r.14.已知:如图,⊙O是梯形ABCD的内切圆,切点为E、F、G、H。求∠DOC的度数.(2) 若梯形的周长为16厘米,上底AD=2厘米,求⊙O 的直径的长.15.已知:PA、PB分别切⊙O于A、B两点,连结AB,PO与⊙O和AB分别交于D、C点,PA=10cm, ∠APB=60°,求CD的长.16.如图,P为⊙O外一点,PA切⊙O于A,PB切⊙O于B,BC为直径.求证:AC∥OP.17.已知AD为△ABC的角平分线,过A、B、D三点作⊙O,EF切⊙O于D,交AC于E.求证:CD2=CE·AC.18.如图7-109,已知PBA是⊙O的割线,PC是圆的切线,C为切点,过A引AD∥PC交圆于点D,连CD、BD、CA,求证(1)CD=CA,(2)CD2=PA·BD.19.如图7-108,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分∠CAB,且AE=2,求∠C的度数和△ABC各边的长. 20. 已知:如图,ABCD是⊙O的内接四边形,过C作DB的平行线,交AB的延长线于E.求证BE·AD=BC·CD. 21. 已知:如图,AB是⊙O直径,CD切⊙O于C,BD⊥CD于D,CE⊥AB于E.求证CD2=AE·EB.22.已知:如图,△ABC是⊙O的内接三角形,AD是⊙O的切线,CE∥AD交AB于E.求证AC2=AE·AB.23.已知:如图,AB是圆的弦,DE切圆于C,AD⊥DE于D,BE⊥DE于E,CF⊥AB于F.求证:CF2=AD· BE. 24.如图,在RtΔABC中,∠C=900,AC=4,BC=3,CD为直径的⊙O与AB相切于E,求⊙O的半径.
————教学具体内容要有提示或附后
课堂检测 听课及知识掌握情况反馈_________________________________________________________。测试题(累计不超过20分钟)_______道;成绩_______;教学需:加快□;保持□;放慢□;增加内容□
课后巩固 作业_____题; 巩固复习____________________ ; 预习布置_____________________
签字 教学组长签字: 学习管理师:
老师课后赏识评价 老师最欣赏的地方:
老师想知道的事情:
老师的建议:
教学目标 知识点:直线与圆相切的判定考点:直线与圆相切的应用能力:方法:
难点重点 直线与圆相切的判定 切线长定理、
课堂教学过程 课前检查 作业完成情况:优□ 良□ 中□ 差□ 建议__________________________________________
过程 直线和圆的位置关系(A)一、填空:1.如图1,AB、CD相交于P,PA>PB,AB=12cm,P将CD分成4cm和5cm两部分, 那么PA=____cm.2.如图2,PC为⊙O的切线,C为切点,PAB为⊙O的割线,若PA=4cm,AB=5cm,那么PC=_____cm. (1) (2) (3) (4) (5)3.如图3,⊙O的半径为3cm,OP=6cm,PC、PD切⊙O于C、D, 那么∠CPD=_____,PC=____cm..4.如图4, D为弦AB的中点,CD⊥AB于D,AB=10cm、CD=3cm,那么⊙O的半径为____cm。5.如图5,Rt△ABC中,∠ACB=90°,AC=5,BC=12,以C为圆心,CA为半径做⊙C,交AB于D,交BC于E。那么AD=_______。6.如图7-104,AB、AC是⊙O的两条切线,切点为B、C,D是优弧上一点,已知∠BAC=80°,那么∠BDC= 度.7.如图7-105,AB是⊙O的直径,C、D是⊙O上的点,∠BAC=20°,=,DE是⊙O的切线,则∠EDC= . (6)8.如图7-106,在圆的内接四边形ABCD中,AC平分∠BAD,EF切⊙O于C点,那么图中与∠DCF相等的角有______个.9.如图6,AB和AC分别切⊙O于B、C,AB=50,DE是⊙O的切线,与AB、AC分别交于DE,则△ADE的周长为_________.10.圆外切四边形ABCD中,AB=2,BC=3,CD=4,则AD=_______.11.从圆外一点向圆所作两条切线的夹角为60°,切线长是10厘米,则圆的半径长为______。12.圆外切等腰梯形周长为24,则这个梯形的腰长为______,中位线长为_______。二、解下列各题:13.已知: Rt△ABC中, ∠B=900,BC=a,AC=b,AB=c, ⊙O与各边相于D、E、F。求Rt△ABC的内切圆的半径r.14.已知:如图,⊙O是梯形ABCD的内切圆,切点为E、F、G、H。求∠DOC的度数.(2) 若梯形的周长为16厘米,上底AD=2厘米,求⊙O 的直径的长.15.已知:PA、PB分别切⊙O于A、B两点,连结AB,PO与⊙O和AB分别交于D、C点,PA=10cm, ∠APB=60°,求CD的长.16.如图,P为⊙O外一点,PA切⊙O于A,PB切⊙O于B,BC为直径.求证:AC∥OP.17.已知AD为△ABC的角平分线,过A、B、D三点作⊙O,EF切⊙O于D,交AC于E.求证:CD2=CE·AC.18.如图7-109,已知PBA是⊙O的割线,PC是圆的切线,C为切点,过A引AD∥PC交圆于点D,连CD、BD、CA,求证(1)CD=CA,(2)CD2=PA·BD.19.如图7-108,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分∠CAB,且AE=2,求∠C的度数和△ABC各边的长. 20. 已知:如图,ABCD是⊙O的内接四边形,过C作DB的平行线,交AB的延长线于E.求证BE·AD=BC·CD. 21. 已知:如图,AB是⊙O直径,CD切⊙O于C,BD⊥CD于D,CE⊥AB于E.求证CD2=AE·EB.22.已知:如图,△ABC是⊙O的内接三角形,AD是⊙O的切线,CE∥AD交AB于E.求证AC2=AE·AB.23.已知:如图,AB是圆的弦,DE切圆于C,AD⊥DE于D,BE⊥DE于E,CF⊥AB于F.求证:CF2=AD· BE. 24.如图,在RtΔABC中,∠C=900,AC=4,BC=3,CD为直径的⊙O与AB相切于E,求⊙O的半径.
————教学具体内容要有提示或附后
课堂检测 听课及知识掌握情况反馈_________________________________________________________。测试题(累计不超过20分钟)_______道;成绩_______;教学需:加快□;保持□;放慢□;增加内容□
课后巩固 作业_____题; 巩固复习____________________ ; 预习布置_____________________
签字 教学组长签字: 学习管理师:
老师课后赏识评价 老师最欣赏的地方:
老师想知道的事情:
老师的建议:
同课章节目录
