(试题2)12.1轴对称
文档属性
| 名称 | (试题2)12.1轴对称 |

|
|
| 格式 | zip | ||
| 文件大小 | 515.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-16 00:00:00 | ||
图片预览


文档简介
七彩中考题系列:轴对称
一、选择题
1. 目 (2006 宿迁课改)下列图案中,不是轴对称图形的是( )
A. B. C. D.
2. (2006 天津非课改)下列图形中,为轴对称图形的是( )
A. B. C. D.
3. (2006 衡阳课改)下列图形中,是轴对称图形的个数为( )
A.0个 B.1个 C.2个 C.3个
4. (2006 沈阳课改)图是几种汽车的标志,其中是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
5. (2006 山西吕梁课改)下列图形中是轴对称图形的是( )
A. B. C. D.
6. 期工程(2006 辽宁十一市课改)将一个正方形纸片依次按图(1),图(2)方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所看到的图案是( )
7. (2006 河南非课改)下列图形中,是轴对称图形的有( )
A.个 B.个 C.个 D.个
8. (2006 吉林非课改)下列图形中,不是轴对称图形的是( )
9. (2006 无锡课改)在下面四个图案中,如果不考虑图中的文字和字母,那么不是轴对称图形的是( )
A. B. C. D.
10. (2006 吉林课改)下列由数字组成的图形中,是轴对称图形的是( )
11. (2006 山西临汾)将一张菱形纸片,按下图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
( http: / / www. )
12. (2006 深圳课改)下列图形中,是轴对称图形的为( )
二,填空题
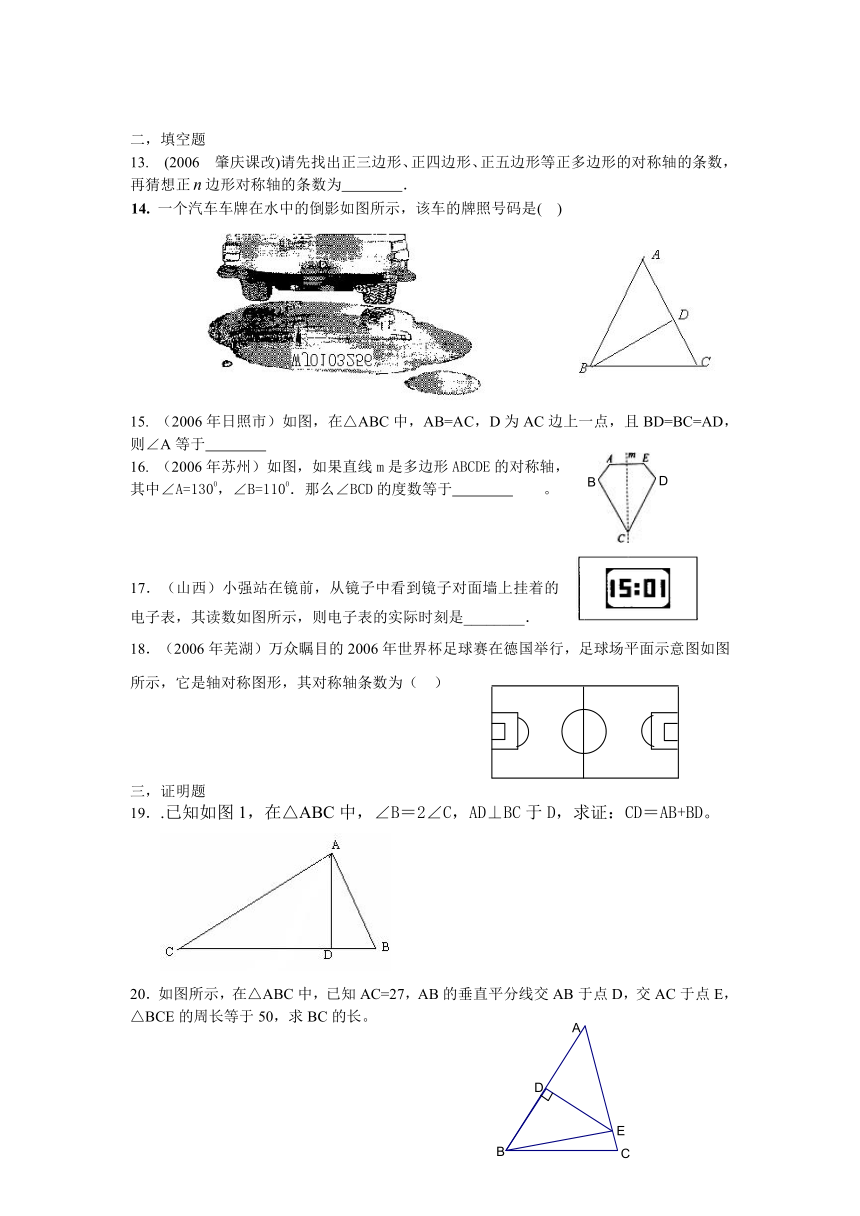
13. (2006 肇庆课改)请先找出正三边形、正四边形、正五边形等正多边形的对称轴的条数,再猜想正边形对称轴的条数为 .
14. 一个汽车车牌在水中的倒影如图所示,该车的牌照号码是( )
15. (2006年日照市)如图,在△ABC中,AB=AC,D为AC边上一点,且BD=BC=AD, 则∠A等于
16. (2006年苏州)如图,如果直线m是多边形ABCDE的对称轴,
其中∠A=1300,∠B=1100.那么∠BCD的度数等于 。
17.(山西)小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是________.
18.(2006年芜湖)万众瞩目的2006年世界杯足球赛在德国举行,足球场平面示意图如图所示,它是轴对称图形,其对称轴条数为( )
三,证明题
19..已知如图1,在△ABC中,∠B=2∠C,AD⊥BC于D,求证:CD=AB+BD。
20.如图所示,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长。
21、如图所示,在△ABC中,D为BC上的一点,连结AD,点E在AD上,并且∠1=∠2,∠3=∠4。求证:AD垂直平分BC。
22如图,⊿ABC中∠BAC=120 ,AD⊥BC于D,AB+BD=DC,则∠C的大小是?(希望杯赛题)
( http: / / www. )
一、选择题
1. C
2. B
3. C
4. B
5. C
6. D
7. C
8. D
9. B
10. A
11. A
12. D
二、填空题
13.n
14. WJ0103256,
15. 解:设∠A=x,因为AB=AC,且BD=BC=AD,所以∠ABC=∠C,∠A=∠ABD=x,∠BDC=∠C。又因为∠BDC=∠A+∠ABD=2 x,所以∠ABD=∠CBD=x。又因为∠A+∠ABC+∠C=180 o,所以x+2x+2x=180 o,所以x=36o,
16. 1分析:此题考查的是轴对称图形性质的运用。要求∠BCD的度数,由∠A=1300,∠B=1100,可求得∠D和∠E,再由五边形的内角和以及轴对称图形的性质可求出∠BCD。
解:因为多边形ABCDE是五边形,所以∠A+∠B+∠C+∠D+∠E=5400。又因为直线m是多边形ABCDE的对称轴,且∠A=1300,∠B=1100,所以∠D=∠B=1100,∠E=∠A=1300。所以∠BCD=5400-1300×2-1100×2=600,
17.10:21(提示:可从反面读数)
18.析解:此题考查的是根据轴对称图形的定义找对称轴的条数。经过判断知足球场示意图有2条对称轴, 点评:轴对称图形的对称轴有时不止一条,分析问题时要考虑全面。
三,证明题
19析证:由于已知AD⊥BC,欲证CD=AB+BD,AB、BD不在同一直线上,所以通过构造垂直平分线可将AB、BD转换到同直线上,进而证明。
在CD上截取DE=BD,连结AE,则AD为BE的垂直平分线,则AB=AE。
所以∠B=∠AEB,
因为∠B=2∠C,∠AEB=∠C+∠EAC,
所以∠C=∠EAC,所以CE=AE=AB,
因为CD=CE+ED,所以CD=AB+BD。
规律总结:充分利用已知条件AD⊥BC和∠B=2∠C从而构造AD为某一线段的垂直平分线,目的是构造等腰三角形,而其中的角的2倍关系常构造一个以小角为底角的等腰三角形,利用三角形的外角性质可以解决问题。
20.分析:题中给出了线段垂直平分线这个条件,所以可以考虑运用其性质定理,从而得出AE=BE,把BE与AE进行等量代换,再根据△BCE的周长及AC的长,可求出BC的长。
解:
因为ED是线段AB的垂直平分线,
所以BE=AE。
因为△BCE的周长等于50,
即BE+EC+BC=50,
所以AE+EC+BC=50。
又因为AE+EC=AC=27,
所以BC=50-27=23。
21分析:本道题目可以选取第二种判断方法,也就是通过得出EB=EC,AB=AC,从而证明出AD垂直平分BC。
证明:
因为∠1=∠2,
所以EB=EC,
所以点E在线段BC的垂直平分线上。
又因为∠1=∠2,∠3=∠4,
所以∠ABC=∠ACB,
所以点A也在线段BC的垂直平分线上。
所以AD垂直平分BC。
22解:延长DB到E,使得DE=DC连AE,∵AD⊥BC
∴AE=AC,∠C=∠E
又∵AB+BD=DC=DE
∴AB=BE,∠E=∠BAE
设∠C的度数为x
由三角形内角和定理得∠C+∠E+∠EAB+∠BAC=180 ,即3x+120 =180
解得x=20 ,
(向上对折)
图(1)
(向右对折)
图(2)
图(3)
图(4)
A.
B.
C.
D.
A.
B.
C.
D.
A.
B.
C.
D.
①
②
③
④
A.
B.
C.
D.
A.
B.
C.
D.
一、选择题
1. 目 (2006 宿迁课改)下列图案中,不是轴对称图形的是( )
A. B. C. D.
2. (2006 天津非课改)下列图形中,为轴对称图形的是( )
A. B. C. D.
3. (2006 衡阳课改)下列图形中,是轴对称图形的个数为( )
A.0个 B.1个 C.2个 C.3个
4. (2006 沈阳课改)图是几种汽车的标志,其中是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
5. (2006 山西吕梁课改)下列图形中是轴对称图形的是( )
A. B. C. D.
6. 期工程(2006 辽宁十一市课改)将一个正方形纸片依次按图(1),图(2)方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所看到的图案是( )
7. (2006 河南非课改)下列图形中,是轴对称图形的有( )
A.个 B.个 C.个 D.个
8. (2006 吉林非课改)下列图形中,不是轴对称图形的是( )
9. (2006 无锡课改)在下面四个图案中,如果不考虑图中的文字和字母,那么不是轴对称图形的是( )
A. B. C. D.
10. (2006 吉林课改)下列由数字组成的图形中,是轴对称图形的是( )
11. (2006 山西临汾)将一张菱形纸片,按下图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
( http: / / www. )
12. (2006 深圳课改)下列图形中,是轴对称图形的为( )
二,填空题
13. (2006 肇庆课改)请先找出正三边形、正四边形、正五边形等正多边形的对称轴的条数,再猜想正边形对称轴的条数为 .
14. 一个汽车车牌在水中的倒影如图所示,该车的牌照号码是( )
15. (2006年日照市)如图,在△ABC中,AB=AC,D为AC边上一点,且BD=BC=AD, 则∠A等于
16. (2006年苏州)如图,如果直线m是多边形ABCDE的对称轴,
其中∠A=1300,∠B=1100.那么∠BCD的度数等于 。
17.(山西)小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是________.
18.(2006年芜湖)万众瞩目的2006年世界杯足球赛在德国举行,足球场平面示意图如图所示,它是轴对称图形,其对称轴条数为( )
三,证明题
19..已知如图1,在△ABC中,∠B=2∠C,AD⊥BC于D,求证:CD=AB+BD。
20.如图所示,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长。
21、如图所示,在△ABC中,D为BC上的一点,连结AD,点E在AD上,并且∠1=∠2,∠3=∠4。求证:AD垂直平分BC。
22如图,⊿ABC中∠BAC=120 ,AD⊥BC于D,AB+BD=DC,则∠C的大小是?(希望杯赛题)
( http: / / www. )
一、选择题
1. C
2. B
3. C
4. B
5. C
6. D
7. C
8. D
9. B
10. A
11. A
12. D
二、填空题
13.n
14. WJ0103256,
15. 解:设∠A=x,因为AB=AC,且BD=BC=AD,所以∠ABC=∠C,∠A=∠ABD=x,∠BDC=∠C。又因为∠BDC=∠A+∠ABD=2 x,所以∠ABD=∠CBD=x。又因为∠A+∠ABC+∠C=180 o,所以x+2x+2x=180 o,所以x=36o,
16. 1分析:此题考查的是轴对称图形性质的运用。要求∠BCD的度数,由∠A=1300,∠B=1100,可求得∠D和∠E,再由五边形的内角和以及轴对称图形的性质可求出∠BCD。
解:因为多边形ABCDE是五边形,所以∠A+∠B+∠C+∠D+∠E=5400。又因为直线m是多边形ABCDE的对称轴,且∠A=1300,∠B=1100,所以∠D=∠B=1100,∠E=∠A=1300。所以∠BCD=5400-1300×2-1100×2=600,
17.10:21(提示:可从反面读数)
18.析解:此题考查的是根据轴对称图形的定义找对称轴的条数。经过判断知足球场示意图有2条对称轴, 点评:轴对称图形的对称轴有时不止一条,分析问题时要考虑全面。
三,证明题
19析证:由于已知AD⊥BC,欲证CD=AB+BD,AB、BD不在同一直线上,所以通过构造垂直平分线可将AB、BD转换到同直线上,进而证明。
在CD上截取DE=BD,连结AE,则AD为BE的垂直平分线,则AB=AE。
所以∠B=∠AEB,
因为∠B=2∠C,∠AEB=∠C+∠EAC,
所以∠C=∠EAC,所以CE=AE=AB,
因为CD=CE+ED,所以CD=AB+BD。
规律总结:充分利用已知条件AD⊥BC和∠B=2∠C从而构造AD为某一线段的垂直平分线,目的是构造等腰三角形,而其中的角的2倍关系常构造一个以小角为底角的等腰三角形,利用三角形的外角性质可以解决问题。
20.分析:题中给出了线段垂直平分线这个条件,所以可以考虑运用其性质定理,从而得出AE=BE,把BE与AE进行等量代换,再根据△BCE的周长及AC的长,可求出BC的长。
解:
因为ED是线段AB的垂直平分线,
所以BE=AE。
因为△BCE的周长等于50,
即BE+EC+BC=50,
所以AE+EC+BC=50。
又因为AE+EC=AC=27,
所以BC=50-27=23。
21分析:本道题目可以选取第二种判断方法,也就是通过得出EB=EC,AB=AC,从而证明出AD垂直平分BC。
证明:
因为∠1=∠2,
所以EB=EC,
所以点E在线段BC的垂直平分线上。
又因为∠1=∠2,∠3=∠4,
所以∠ABC=∠ACB,
所以点A也在线段BC的垂直平分线上。
所以AD垂直平分BC。
22解:延长DB到E,使得DE=DC连AE,∵AD⊥BC
∴AE=AC,∠C=∠E
又∵AB+BD=DC=DE
∴AB=BE,∠E=∠BAE
设∠C的度数为x
由三角形内角和定理得∠C+∠E+∠EAB+∠BAC=180 ,即3x+120 =180
解得x=20 ,
(向上对折)
图(1)
(向右对折)
图(2)
图(3)
图(4)
A.
B.
C.
D.
A.
B.
C.
D.
A.
B.
C.
D.
①
②
③
④
A.
B.
C.
D.
A.
B.
C.
D.
