江苏省泰州市两校2020-2021学年高一上学期期中联考数学试题 Word版含答案
文档属性
| 名称 | 江苏省泰州市两校2020-2021学年高一上学期期中联考数学试题 Word版含答案 | 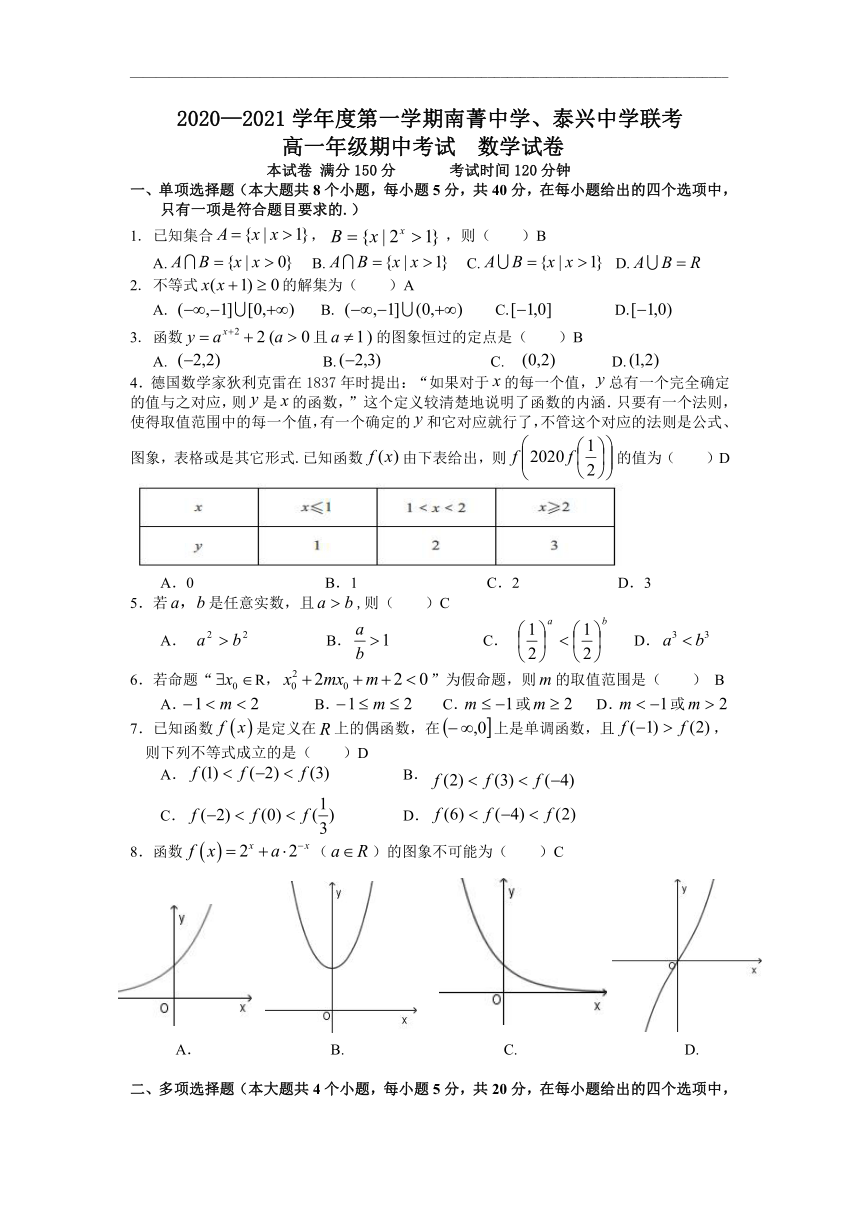 | |
| 格式 | doc | ||
| 文件大小 | 680.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 11:22:45 | ||
图片预览



文档简介
____________________________________________________________________________________________
2020—2021学年度第一学期南菁中学、泰兴中学联考
高一年级期中考试 数学试卷
本试卷 满分150分 考试时间120分钟
一、单项选择题(本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合,,则( )B
A. B. C. D.
2. 不等式的解集为( )A
A. B. C. D.
3. 函数且的图象恒过的定点是( )B
A. B. C. D.
4.德国数学家狄利克雷在1837年时提出:“如果对于的每一个值,总有一个完全确定的值与之对应,则是的函数,”这个定义较清楚地说明了函数的内涵.只要有一个法则,使得取值范围中的每一个值,有一个确定的和它对应就行了,不管这个对应的法则是公式、图象,表格或是其它形式.已知函数由下表给出,则的值为( )D
A.0 B.1 C.2 D.3
5.若是任意实数,且,则( )C
A. B. C. D.
6.若命题“R,”为假命题,则的取值范围是( ) B
A. B. C.或 D.或
7.已知函数是定义在上的偶函数,在上是单调函数,且,则下列不等式成立的是( )D
A. B.
C. D.
8.函数()的图象不可能为( )C
A. B. C. D.
二、多项选择题(本大题共4个小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目要求,全部选对得5分,选对但不全的得3分,有选错的得0分.)
9.如果,那么( )AD
A. B. C. D.
下列函数中,在上为增函数的有( )CD
A. B. C. D.
11.下列说法正确的有( )ACD
A. 命题“,”的否定是“,”
B.“”是“”的充分不必要条件
C.“”是“关于的方程有一正根和一负根”的充要条件
D.已知正数满足,则的最小值为
12.设函数,则下列命题中正确的有 ( )ABC
A.若,则
B.方程可能有三个实数根
C.当时,函数在是单调增函数
D.当时,函数在上有最小值
三、填空题(本大题共4个小题,每小题5分,共20分)
13.函数的定义域为 .
14.已知函数,则的最小值为 .
15. 已知幂函数过点,则 .
16.设函数,若,且,则的最小值为 .
四、解答题(共6小题,共70分. 解答题应写出文字说明,证明过程或演算步骤)
17.(本小题满分 10分)
(1)计算: ;
(2)已知,求.
17.解:(1)原式=. ……………………5分
(2)∵,∴,…………………………………………7分
∴,
又,…………………………………9分
∴ 原式.…………………………………………………………………………10分
18.(本小题满分12分)
已知集合,且.
(1)若是的充分条件,求实数的取值范围;
(2)若命题“”为真命题,求实数的取值范围.
18.解:(1)∵,∴,………………………2分
∵是的充分条件, ∴,∴,…………………………………4分
∴,∴实数的取值范围为.……………………………………………6分
(2)∵命题“”为真命题,∴或,………………………………8分
解得或.………………………………………………………………………10分
又∵,∴实数的取值范围为.………………………………12分
(本小题满分12分)
新型冠状病毒感染的肺炎治疗过程中,需要某医药公司生产的某种药品.此药品的年固定成本为万元,每生产千件需另投入成本万元.当年产量不足千件时,;当年产量不小于千件时,.每千件商品售价为万元.在疫情期间,该公司的药品能全部售完.
写出年利润(万元)关于年产量(千件)的函数解析式;
(利润 = 销售收入成本)
(2)该公司决定将此药品所获利润的用来捐赠防疫物资.当年产量为多少千件时,该公司在这一药品的生产中所获利润最大?此时可捐赠多少万元的物资款?
19.解:(1)当时,,
…………………………………………………………………………………………………2分
当时,,…4分
所以.…………………………6分
(不写扣1分)
当时,,
此时,当时,取得最大值万元;…………………………………………8分
当时,,
当且仅当时等号成立,此时,当时,取得最大值万元.…10分
由于,所以当年产量为千件时,该公司在这一药品的生产中所获利润最大,此时可捐赠万元的物资款. …………12分
20.(本小题满分12分)
若实数满足,则称比远离.
若比远离0,求的取值范围;
已知,求证:;
(3)对任意两个不相等的正实数,求证:比远离.
20.解:(1)由题意得 或
…………………………3分
(2)∵,∴,当且仅当时取等号. …5分
(其他方式证明同样给分)
(3)由(2),又不相等,所以 ……………6分
因为,且不相等,所以…8分
所以
………………………10分
所以所以比远离 …12分
21.(本小题满分12分)
已知函数(是自然对数的底).
(1)若,判断的奇偶性,并说明理由;
(2)若函数为奇函数,当时,恒成立,求实数的取值范围.
21.解:(1)若,则,
∵,,∴,且,
∴既不是奇函数,也不是偶函数. …………………………………………4分
(结论对,但理由不充分的扣2分)
(2)为奇函数,,
,,∴,………………………………………6分
(用特值做不检验的扣1分)
,
因为,因为,所以,(不说明扣1分)
所以,…………………8分
又,,………………10分
当且仅当即时取最小值. …………………………11分
所以. ………………………………………12分
22.(本小题满分12分)
已知函数(为实常数).
(1)若函数图象上动点到定点的距离的最小值为,求实数的值;
(参考公式:已知平面上两点,,则、两点间的距离公式为
)
(2)若函数在区间上是增函数,试用函数单调性的定义求实数的取值范围;
(3)设,若不等式在时有解,求实数的取值范围.
22.解:(1)∵,∴
∴
当时,解得;当时,解得.
或. ………………………………3分
设区间上上的任意两个值,且,
∵函数在区间上是增函数,∴,
∴,
∵,∴,
∴,即, ………………………………5分
又∴,的取值范围. …………………………7分
(3)由,得,
,令,记,
∵不等式在时有解,∴时,有解,
∴,……………………………………………………9分
当,即时,;
当,即时,;
综上, 当时,,
当时, . ………………………………12分
2020—2021学年度第一学期南菁中学、泰兴中学联考
高一年级期中考试 数学试卷
本试卷 满分150分 考试时间120分钟
一、单项选择题(本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合,,则( )B
A. B. C. D.
2. 不等式的解集为( )A
A. B. C. D.
3. 函数且的图象恒过的定点是( )B
A. B. C. D.
4.德国数学家狄利克雷在1837年时提出:“如果对于的每一个值,总有一个完全确定的值与之对应,则是的函数,”这个定义较清楚地说明了函数的内涵.只要有一个法则,使得取值范围中的每一个值,有一个确定的和它对应就行了,不管这个对应的法则是公式、图象,表格或是其它形式.已知函数由下表给出,则的值为( )D
A.0 B.1 C.2 D.3
5.若是任意实数,且,则( )C
A. B. C. D.
6.若命题“R,”为假命题,则的取值范围是( ) B
A. B. C.或 D.或
7.已知函数是定义在上的偶函数,在上是单调函数,且,则下列不等式成立的是( )D
A. B.
C. D.
8.函数()的图象不可能为( )C
A. B. C. D.
二、多项选择题(本大题共4个小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目要求,全部选对得5分,选对但不全的得3分,有选错的得0分.)
9.如果,那么( )AD
A. B. C. D.
下列函数中,在上为增函数的有( )CD
A. B. C. D.
11.下列说法正确的有( )ACD
A. 命题“,”的否定是“,”
B.“”是“”的充分不必要条件
C.“”是“关于的方程有一正根和一负根”的充要条件
D.已知正数满足,则的最小值为
12.设函数,则下列命题中正确的有 ( )ABC
A.若,则
B.方程可能有三个实数根
C.当时,函数在是单调增函数
D.当时,函数在上有最小值
三、填空题(本大题共4个小题,每小题5分,共20分)
13.函数的定义域为 .
14.已知函数,则的最小值为 .
15. 已知幂函数过点,则 .
16.设函数,若,且,则的最小值为 .
四、解答题(共6小题,共70分. 解答题应写出文字说明,证明过程或演算步骤)
17.(本小题满分 10分)
(1)计算: ;
(2)已知,求.
17.解:(1)原式=. ……………………5分
(2)∵,∴,…………………………………………7分
∴,
又,…………………………………9分
∴ 原式.…………………………………………………………………………10分
18.(本小题满分12分)
已知集合,且.
(1)若是的充分条件,求实数的取值范围;
(2)若命题“”为真命题,求实数的取值范围.
18.解:(1)∵,∴,………………………2分
∵是的充分条件, ∴,∴,…………………………………4分
∴,∴实数的取值范围为.……………………………………………6分
(2)∵命题“”为真命题,∴或,………………………………8分
解得或.………………………………………………………………………10分
又∵,∴实数的取值范围为.………………………………12分
(本小题满分12分)
新型冠状病毒感染的肺炎治疗过程中,需要某医药公司生产的某种药品.此药品的年固定成本为万元,每生产千件需另投入成本万元.当年产量不足千件时,;当年产量不小于千件时,.每千件商品售价为万元.在疫情期间,该公司的药品能全部售完.
写出年利润(万元)关于年产量(千件)的函数解析式;
(利润 = 销售收入成本)
(2)该公司决定将此药品所获利润的用来捐赠防疫物资.当年产量为多少千件时,该公司在这一药品的生产中所获利润最大?此时可捐赠多少万元的物资款?
19.解:(1)当时,,
…………………………………………………………………………………………………2分
当时,,…4分
所以.…………………………6分
(不写扣1分)
当时,,
此时,当时,取得最大值万元;…………………………………………8分
当时,,
当且仅当时等号成立,此时,当时,取得最大值万元.…10分
由于,所以当年产量为千件时,该公司在这一药品的生产中所获利润最大,此时可捐赠万元的物资款. …………12分
20.(本小题满分12分)
若实数满足,则称比远离.
若比远离0,求的取值范围;
已知,求证:;
(3)对任意两个不相等的正实数,求证:比远离.
20.解:(1)由题意得 或
…………………………3分
(2)∵,∴,当且仅当时取等号. …5分
(其他方式证明同样给分)
(3)由(2),又不相等,所以 ……………6分
因为,且不相等,所以…8分
所以
………………………10分
所以所以比远离 …12分
21.(本小题满分12分)
已知函数(是自然对数的底).
(1)若,判断的奇偶性,并说明理由;
(2)若函数为奇函数,当时,恒成立,求实数的取值范围.
21.解:(1)若,则,
∵,,∴,且,
∴既不是奇函数,也不是偶函数. …………………………………………4分
(结论对,但理由不充分的扣2分)
(2)为奇函数,,
,,∴,………………………………………6分
(用特值做不检验的扣1分)
,
因为,因为,所以,(不说明扣1分)
所以,…………………8分
又,,………………10分
当且仅当即时取最小值. …………………………11分
所以. ………………………………………12分
22.(本小题满分12分)
已知函数(为实常数).
(1)若函数图象上动点到定点的距离的最小值为,求实数的值;
(参考公式:已知平面上两点,,则、两点间的距离公式为
)
(2)若函数在区间上是增函数,试用函数单调性的定义求实数的取值范围;
(3)设,若不等式在时有解,求实数的取值范围.
22.解:(1)∵,∴
∴
当时,解得;当时,解得.
或. ………………………………3分
设区间上上的任意两个值,且,
∵函数在区间上是增函数,∴,
∴,
∵,∴,
∴,即, ………………………………5分
又∴,的取值范围. …………………………7分
(3)由,得,
,令,记,
∵不等式在时有解,∴时,有解,
∴,……………………………………………………9分
当,即时,;
当,即时,;
综上, 当时,,
当时, . ………………………………12分
同课章节目录
