北师大版八年级上册数学 1.1 探索勾股定理(2)(18张PPT)
文档属性
| 名称 | 北师大版八年级上册数学 1.1 探索勾股定理(2)(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 633.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览




文档简介
1.1
探索勾股定理(2)
学习目标:
1.掌握验证勾股定理的两种方法;
2.能应用勾股定理解决一些实际问题.
自学指导一
自学内容:课本4---5页例上方内容
自学时间:8分钟
自学要求:(1)将图1-5,1-6中正方形ABCD的面积用a,b,c表示出来;
(2)利用面积相等列出等式,验证勾股定理.
c
a
b
c
a
b
c
a
b
c
a
b
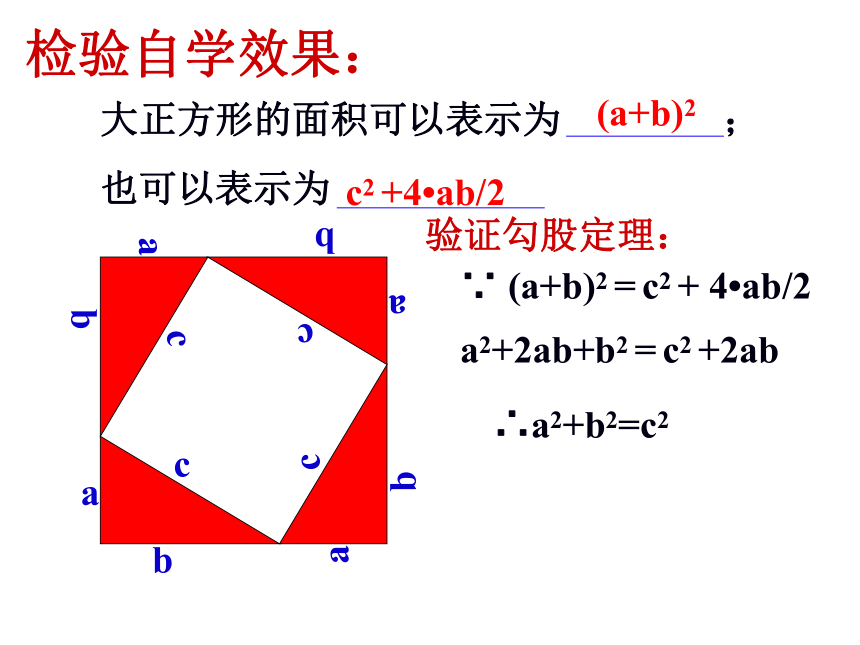
∵ (a+b)2 = c2 + 4?ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4?ab/2
检验自学效果:
验证勾股定理:
c
a
b
c
a
b
c
a
b
c
a
b
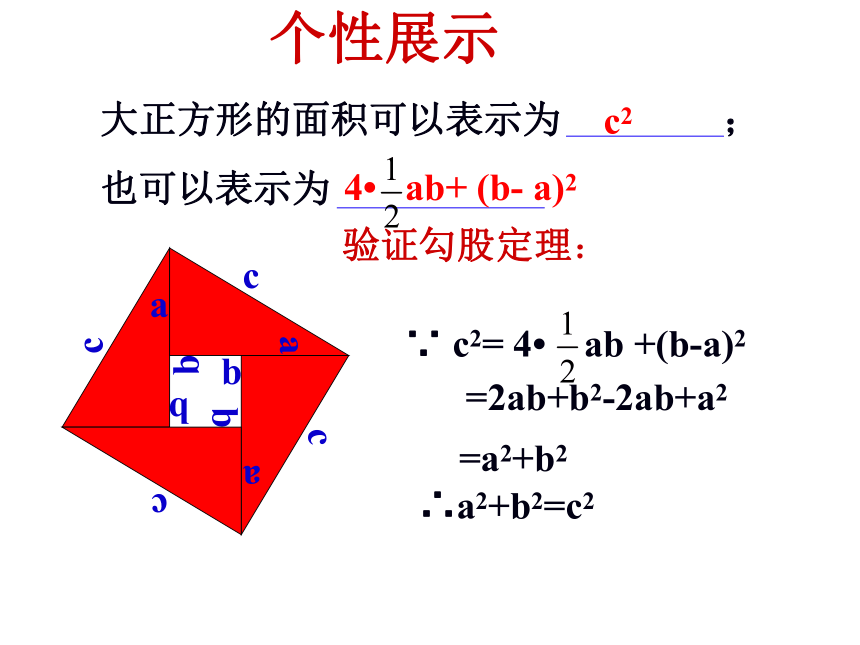
∵ c2= 4? ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4? ab+ (b- a)2
个性展示
验证勾股定理:
巩固训练:
课本7页 数学理解:2
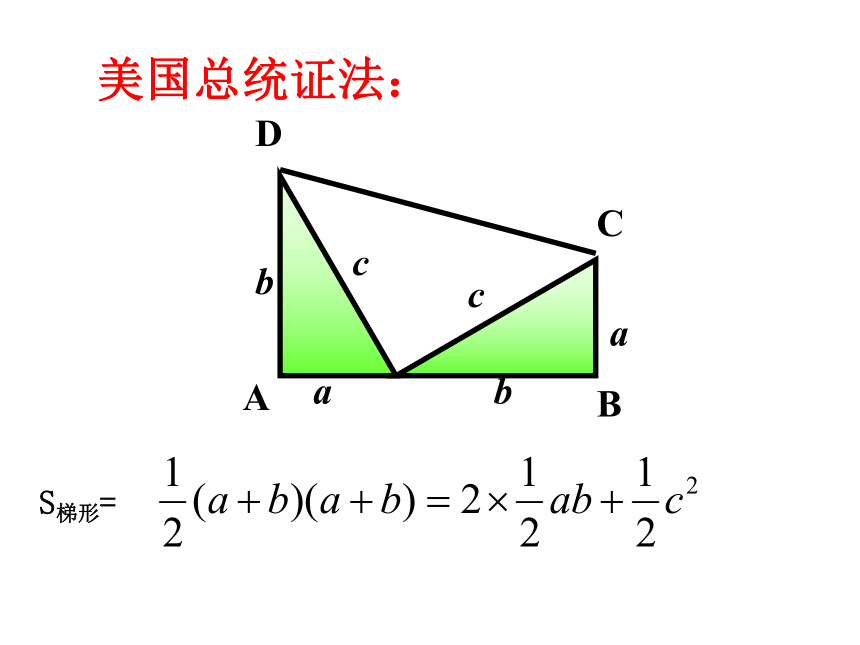
美国总统证法:
b
c
a
b
c
a
A
B
C
D
S梯形=
能力提升:
完成助学第5页 例1
自学指导二:
自学内容:课本例1
自学时间:3分钟
自学要求:
(1)认真阅读例题分析部分,明确要求速度需先求什么;
(2)掌握例题的解题步骤,注意单位的换算
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?
4000
5000
5000
4000
C
B
A
M
P
N
O
Q
30km
40km
50km
120km
自学检测
课本6页随堂练习:1
自学检测
课本6页知识技能:1
4米
3米
如图,受台风麦莎影响,一棵高18米的
大树断裂,树的顶部落在离树根底部6m处,这棵树折断后有多高?
6 m
课本6页“议一议”
达标检测
1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米; B、800米; C、1000米; D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米;
C、 80/13厘米; D、 60/13厘米;
C
D
3.下列阴影部分是一个正方形,求此正方形的面积
15厘米
17厘米
4.一轮船以16海里/小时的速度离A港向东北方向航行,另一艘轮船同时以12海里/小时的速度离A港向西北方向航行,2小时后,两船相距多少海里?
5.等腰三角形底边上的高为8,周长为32,求这个三角形的面积
5、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
X
16-X
D
A
B
C
解:设这个三角形为△ABC,高为AD,设BD为X,则AB为(16-X),
由勾股定理得:
X2+82=(16-X)2
即X2+64=256-32X+X2
∴ X=6
∴ S?ABC=BC?AD/2=2 ×6 ×8/2=48
达标测试
助学第6页自主评价:1----8题
探索勾股定理(2)
学习目标:
1.掌握验证勾股定理的两种方法;
2.能应用勾股定理解决一些实际问题.
自学指导一
自学内容:课本4---5页例上方内容
自学时间:8分钟
自学要求:(1)将图1-5,1-6中正方形ABCD的面积用a,b,c表示出来;
(2)利用面积相等列出等式,验证勾股定理.
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4?ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4?ab/2
检验自学效果:
验证勾股定理:
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2= 4? ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4? ab+ (b- a)2
个性展示
验证勾股定理:
巩固训练:
课本7页 数学理解:2
美国总统证法:
b
c
a
b
c
a
A
B
C
D
S梯形=
能力提升:
完成助学第5页 例1
自学指导二:
自学内容:课本例1
自学时间:3分钟
自学要求:
(1)认真阅读例题分析部分,明确要求速度需先求什么;
(2)掌握例题的解题步骤,注意单位的换算
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?
4000
5000
5000
4000
C
B
A
M
P
N
O
Q
30km
40km
50km
120km
自学检测
课本6页随堂练习:1
自学检测
课本6页知识技能:1
4米
3米
如图,受台风麦莎影响,一棵高18米的
大树断裂,树的顶部落在离树根底部6m处,这棵树折断后有多高?
6 m
课本6页“议一议”
达标检测
1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米; B、800米; C、1000米; D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米;
C、 80/13厘米; D、 60/13厘米;
C
D
3.下列阴影部分是一个正方形,求此正方形的面积
15厘米
17厘米
4.一轮船以16海里/小时的速度离A港向东北方向航行,另一艘轮船同时以12海里/小时的速度离A港向西北方向航行,2小时后,两船相距多少海里?
5.等腰三角形底边上的高为8,周长为32,求这个三角形的面积
5、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
X
16-X
D
A
B
C
解:设这个三角形为△ABC,高为AD,设BD为X,则AB为(16-X),
由勾股定理得:
X2+82=(16-X)2
即X2+64=256-32X+X2
∴ X=6
∴ S?ABC=BC?AD/2=2 ×6 ×8/2=48
达标测试
助学第6页自主评价:1----8题
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
