第七章 平行线的证明 5 三角形内角和定理 (第二课时) 课件(共24张PPT)
文档属性
| 名称 | 第七章 平行线的证明 5 三角形内角和定理 (第二课时) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 19:26:39 | ||
图片预览



文档简介
第七章 平行线的证明
5 三角形内角和定理
(第二课时)
感悟导入
山东省枣庄市第四十一中学
学习目标
1. 会识别三角形的外角,并能运用三角形内角和定理及其两个推论进行简单的计算和证明.
2. 通过小组合作的方式,探索、证明与三角形外角有关的定理,体会一题多解的思维多样性和转化思想,提高总结概括和逻辑推理的能力.
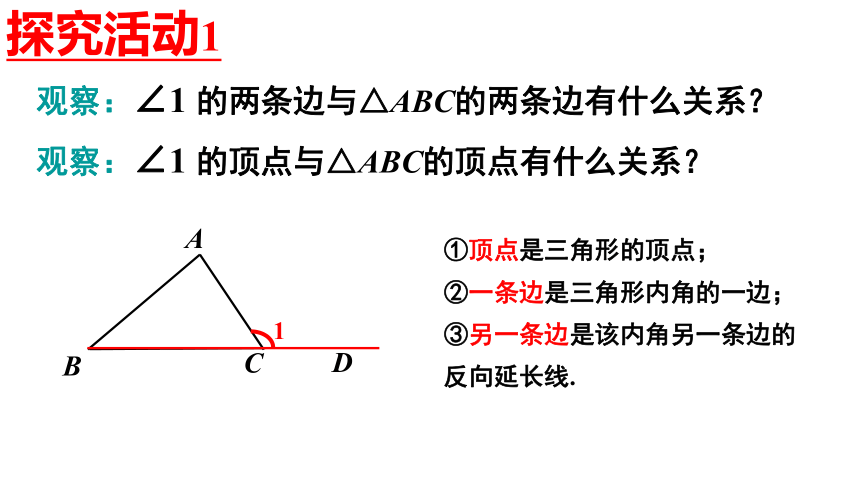
观察:∠1 的两条边与△ABC的两条边有什么关系?
C
B
A
D
探究活动1
1
观察:∠1 的顶点与△ABC的顶点有什么关系?
①顶点是三角形的顶点;
②一条边是三角形内角的一边;
③另一条边是该内角另一条边的
反向延长线.
C
B
A
D
探究活动1
1
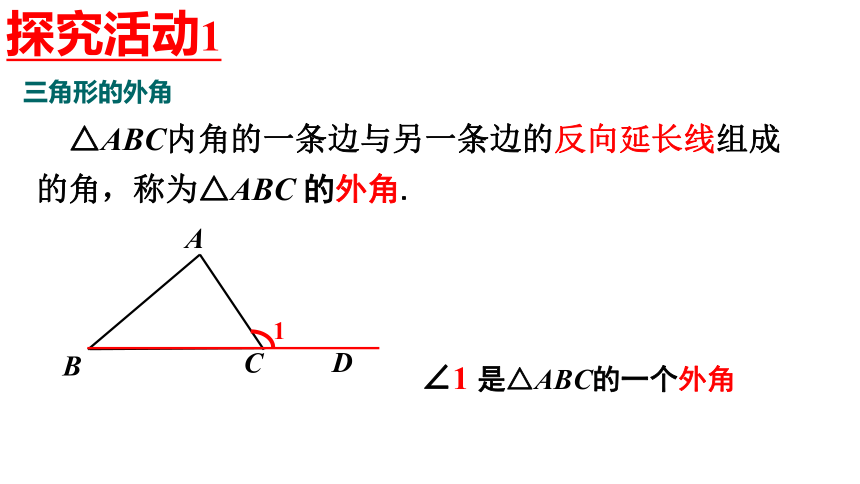
三角形的外角
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC 的外角.
∠1 是△ABC的一个外角
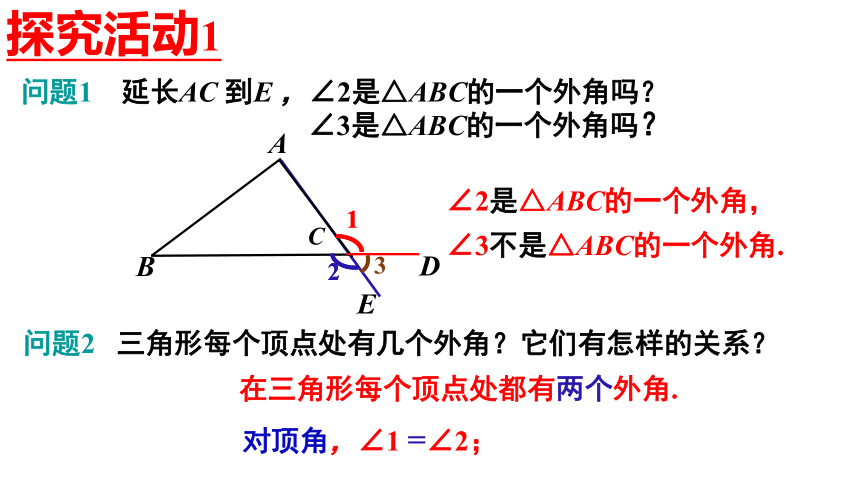
问题1 延长AC 到E ,∠2是△ABC的一个外角吗?
∠3是△ABC的一个外角吗?
E
在三角形每个顶点处都有两个外角.
对顶角,∠1 =∠2;
C
B
A
D
∠2是△ABC的一个外角,
∠3不是△ABC的一个外角.
问题2 三角形每个顶点处有几个外角?它们有怎样的关系?
1
2
3
探究活动1
2
1
F
A
B
C
D
E
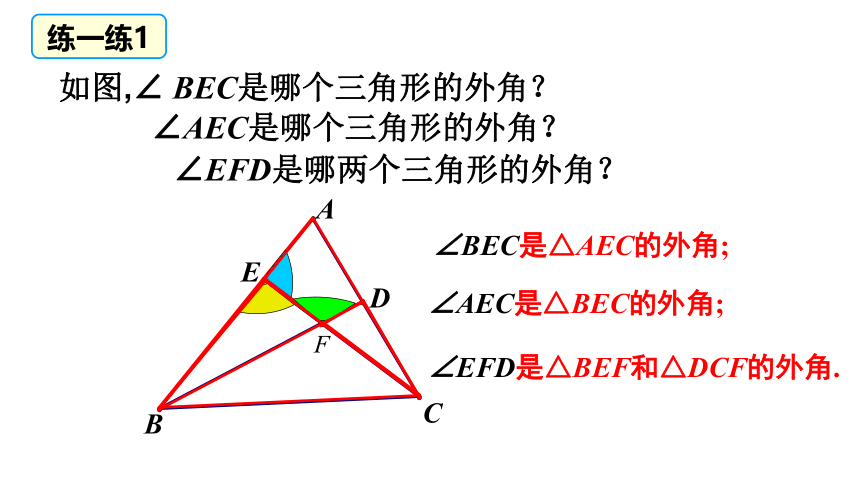
如图,∠ BEC是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
∠AEC是哪个三角形的外角?
∠EFD是哪两个三角形的外角?
练一练1
A
C
B
D
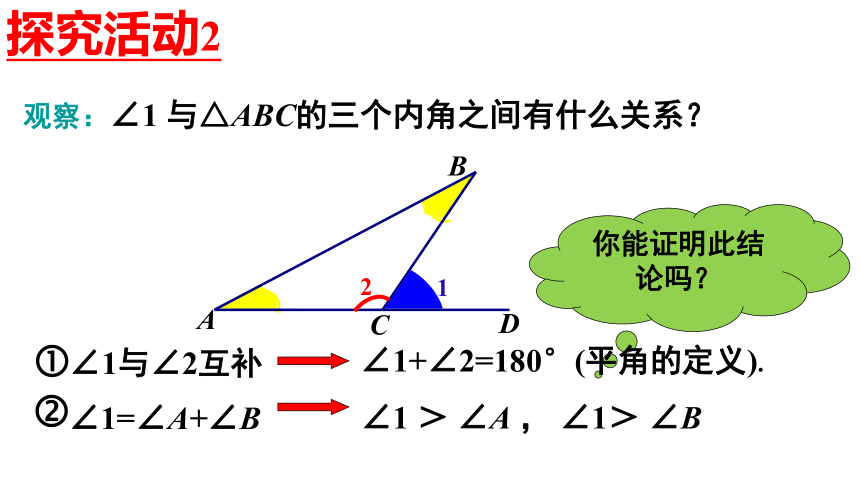
∠1=∠A+∠B
你能证明此结论吗?
观察:∠1 与△ABC的三个内角之间有什么关系?
∠1与∠2互补
探究活动2
1
2
?
?
∠1+∠2=180°(平角的定义).
∠1 > ∠A , ∠1> ∠B
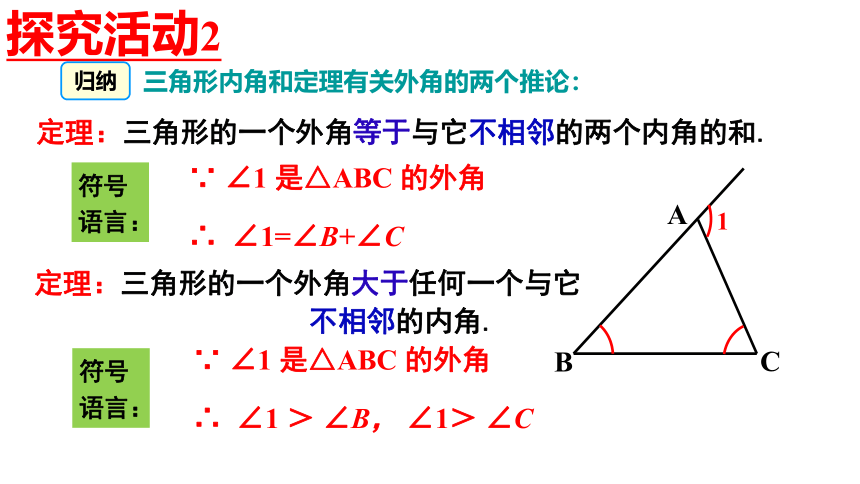
定理:三角形的一个外角等于与它不相邻的两个内角的和.
定理:三角形的一个外角大于任何一个与它
不相邻的内角.
A
B
C
符号语言:
归纳
三角形内角和定理有关外角的两个推论:
∵ ∠1 是△ABC 的外角
∴ ∠1=∠B+∠C
符号语言:
∵ ∠1 是△ABC 的外角
∴ ∠1 > ∠B, ∠1> ∠C
1
探究活动2
?
?
图?
图?
∠2>∠1.
∠3>∠2>∠1.
A
B
C
D
1、如图 , 试比较∠2 、∠1的大小;
1
2
如图 , 试比较∠3 、∠2、 ∠1的大小.
2
3
C
1
A
B
D
E
有奖竞答
练一练2
2、在△ABC中,∠A=45°,外角∠DCA=100°
则∠B= ,∠ACB= .
A
B
C
D
有奖竞答
55°
80°
100°
45°
练一练2
例2 如图,在△ABC中,∠B= ∠C,AD平分外角∠EAC.
求证:AD∥ BC.
A
C
D
B
E
例题运用了定理“内错角相等,两直线平行”
证明:∵∠EAC=∠B+∠C (三角形的一个
外角等于和它不相邻的两个内角的和),
∠B=∠C (已知),
2
3
1
∴∠C= ∠EAC (等式的性质).
∵AD平分 ∠EAC(已知).
∴∠DAC= ∠EAC(角平分线的定义).
∴∠DAC=∠C(等量代换).
∴AD∥ BC(内错角相等,两直线平行).
例3 如图, P是△ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
A
B
C
P
动脑筋
E
例3 如图, P是△ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
证明:如图,延长BP,交AC于点D.
∵ ∠BPC是△PDC的一个外角(外角定义),
∴ ∠BPC >∠PDC(三角形的一个外角
大于任何一个和它不相邻的内角).
A
B
C
P
D
还有其他证明方法吗?
动脑筋
∵ ∠PDC是△ABD的一个外角 (外角定义),
∴ ∠PDC >∠A(三角形的一个外角大于任何
一个和它不相邻的内角).
∴ ∠BPC >∠A .
例3 如图, P是△ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
A
B
C
P
动脑筋
F
1
2
3
4
A
B
D
动脑筋
变式: 如图,已知∠1 =150° 求: ∠A+∠B+∠D 的度数?
C
山东省枣庄市第四十一中学
1
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角(外角的定义),
∴ ∠1=∠B+∠D(三角形的一个外角等于和它不相邻的两个内角的和).
同理可证 ∠2=∠C+∠E
又∵∠A+∠1+∠2=180°(三角形内角和定理).
∴ ∠A+∠B+∠C+∠D+∠E =180°(等式性质).
我能行
F
1
H
2
A
E
D
C
B
通过本节课的共同探究, 我收获了……
再回首
检测进行中……
祝您满载而归!
1、如图,AB // CD,∠A=37°, ∠C=63°,那么 ∠F 等于 ( )
F
A
B
E
C
D
A. 26°
B. 63°
C. 37°
D. 60°
A
达标检测
基础题
达标检测
B
基础题
2、如图,∠1,∠2,∠A 的大小关系是( )
A. ∠A>∠1>∠2
B. ∠2>∠1>∠A
C. ∠A>∠2>∠1
D. ∠2>∠A>∠1
A
C
B
1
2
提高题
达标检测
3、(2014·邵阳中考)如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是 .
E
A
B
C
D
40°
4、已知:D是△ABC边BA延长线上一点,E是AC上一点,BE与CD相交于F,若∠BAC=62°, ∠ACD=35°,∠ABE=20°.
求:(1)∠D度数;
(2)∠BFD度数.
达标检测
拓展题
27°
133°
F
E
C
B
A
D
相信自己
一份耕耘 一份收获
只要付出 一定会有收获!
谢谢!
5 三角形内角和定理
(第二课时)
感悟导入
山东省枣庄市第四十一中学
学习目标
1. 会识别三角形的外角,并能运用三角形内角和定理及其两个推论进行简单的计算和证明.
2. 通过小组合作的方式,探索、证明与三角形外角有关的定理,体会一题多解的思维多样性和转化思想,提高总结概括和逻辑推理的能力.
观察:∠1 的两条边与△ABC的两条边有什么关系?
C
B
A
D
探究活动1
1
观察:∠1 的顶点与△ABC的顶点有什么关系?
①顶点是三角形的顶点;
②一条边是三角形内角的一边;
③另一条边是该内角另一条边的
反向延长线.
C
B
A
D
探究活动1
1
三角形的外角
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC 的外角.
∠1 是△ABC的一个外角
问题1 延长AC 到E ,∠2是△ABC的一个外角吗?
∠3是△ABC的一个外角吗?
E
在三角形每个顶点处都有两个外角.
对顶角,∠1 =∠2;
C
B
A
D
∠2是△ABC的一个外角,
∠3不是△ABC的一个外角.
问题2 三角形每个顶点处有几个外角?它们有怎样的关系?
1
2
3
探究活动1
2
1
F
A
B
C
D
E
如图,∠ BEC是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
∠AEC是哪个三角形的外角?
∠EFD是哪两个三角形的外角?
练一练1
A
C
B
D
∠1=∠A+∠B
你能证明此结论吗?
观察:∠1 与△ABC的三个内角之间有什么关系?
∠1与∠2互补
探究活动2
1
2
?
?
∠1+∠2=180°(平角的定义).
∠1 > ∠A , ∠1> ∠B
定理:三角形的一个外角等于与它不相邻的两个内角的和.
定理:三角形的一个外角大于任何一个与它
不相邻的内角.
A
B
C
符号语言:
归纳
三角形内角和定理有关外角的两个推论:
∵ ∠1 是△ABC 的外角
∴ ∠1=∠B+∠C
符号语言:
∵ ∠1 是△ABC 的外角
∴ ∠1 > ∠B, ∠1> ∠C
1
探究活动2
?
?
图?
图?
∠2>∠1.
∠3>∠2>∠1.
A
B
C
D
1、如图 , 试比较∠2 、∠1的大小;
1
2
如图 , 试比较∠3 、∠2、 ∠1的大小.
2
3
C
1
A
B
D
E
有奖竞答
练一练2
2、在△ABC中,∠A=45°,外角∠DCA=100°
则∠B= ,∠ACB= .
A
B
C
D
有奖竞答
55°
80°
100°
45°
练一练2
例2 如图,在△ABC中,∠B= ∠C,AD平分外角∠EAC.
求证:AD∥ BC.
A
C
D
B
E
例题运用了定理“内错角相等,两直线平行”
证明:∵∠EAC=∠B+∠C (三角形的一个
外角等于和它不相邻的两个内角的和),
∠B=∠C (已知),
2
3
1
∴∠C= ∠EAC (等式的性质).
∵AD平分 ∠EAC(已知).
∴∠DAC= ∠EAC(角平分线的定义).
∴∠DAC=∠C(等量代换).
∴AD∥ BC(内错角相等,两直线平行).
例3 如图, P是△ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
A
B
C
P
动脑筋
E
例3 如图, P是△ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
证明:如图,延长BP,交AC于点D.
∵ ∠BPC是△PDC的一个外角(外角定义),
∴ ∠BPC >∠PDC(三角形的一个外角
大于任何一个和它不相邻的内角).
A
B
C
P
D
还有其他证明方法吗?
动脑筋
∵ ∠PDC是△ABD的一个外角 (外角定义),
∴ ∠PDC >∠A(三角形的一个外角大于任何
一个和它不相邻的内角).
∴ ∠BPC >∠A .
例3 如图, P是△ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
A
B
C
P
动脑筋
F
1
2
3
4
A
B
D
动脑筋
变式: 如图,已知∠1 =150° 求: ∠A+∠B+∠D 的度数?
C
山东省枣庄市第四十一中学
1
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角(外角的定义),
∴ ∠1=∠B+∠D(三角形的一个外角等于和它不相邻的两个内角的和).
同理可证 ∠2=∠C+∠E
又∵∠A+∠1+∠2=180°(三角形内角和定理).
∴ ∠A+∠B+∠C+∠D+∠E =180°(等式性质).
我能行
F
1
H
2
A
E
D
C
B
通过本节课的共同探究, 我收获了……
再回首
检测进行中……
祝您满载而归!
1、如图,AB // CD,∠A=37°, ∠C=63°,那么 ∠F 等于 ( )
F
A
B
E
C
D
A. 26°
B. 63°
C. 37°
D. 60°
A
达标检测
基础题
达标检测
B
基础题
2、如图,∠1,∠2,∠A 的大小关系是( )
A. ∠A>∠1>∠2
B. ∠2>∠1>∠A
C. ∠A>∠2>∠1
D. ∠2>∠A>∠1
A
C
B
1
2
提高题
达标检测
3、(2014·邵阳中考)如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是 .
E
A
B
C
D
40°
4、已知:D是△ABC边BA延长线上一点,E是AC上一点,BE与CD相交于F,若∠BAC=62°, ∠ACD=35°,∠ABE=20°.
求:(1)∠D度数;
(2)∠BFD度数.
达标检测
拓展题
27°
133°
F
E
C
B
A
D
相信自己
一份耕耘 一份收获
只要付出 一定会有收获!
谢谢!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
