北师大七年级下册4.1认识三角形(1) 课件(共29张ppt)
文档属性
| 名称 | 北师大七年级下册4.1认识三角形(1) 课件(共29张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览





文档简介
1
2
3
4
北师大七年级下册
学习目标:
1、通过观察、推理、交流等活动,发展空间观念、推理能力和有条理的表达能力。
2、?结合实例进一步认识三角形的概念及基本要素,能用符号语言表示三角形;?探究发现三角形内角和等于180°;?能按三角形内角大小进行分类。④能用运用直角三角形两锐角互余的性质解决简单的问题。
3、树立几何知识源于客观实际,用于客观实际的观念,激发学习兴趣。
A
D
B
E
C
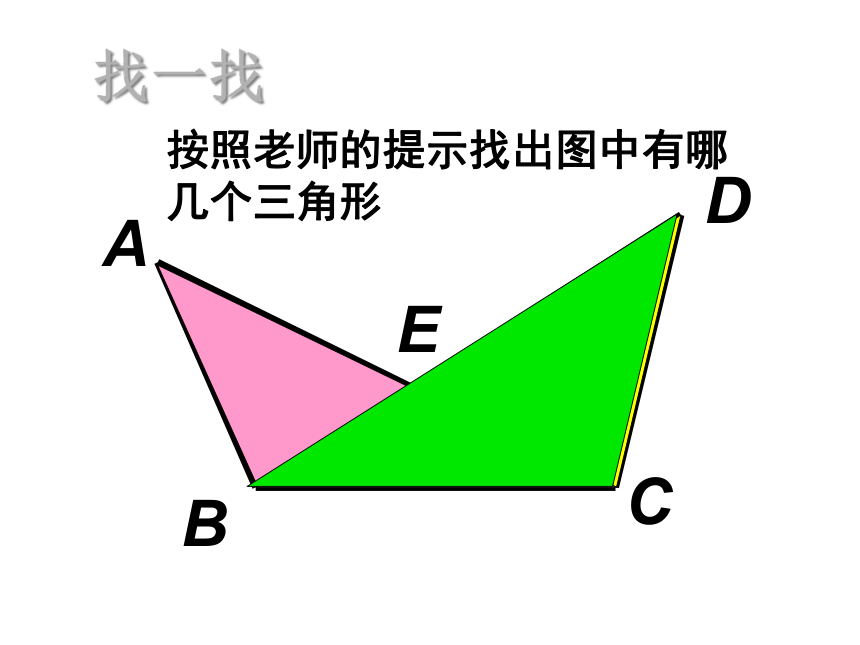
找一找
按照老师的提示找出图中有哪几个三角形
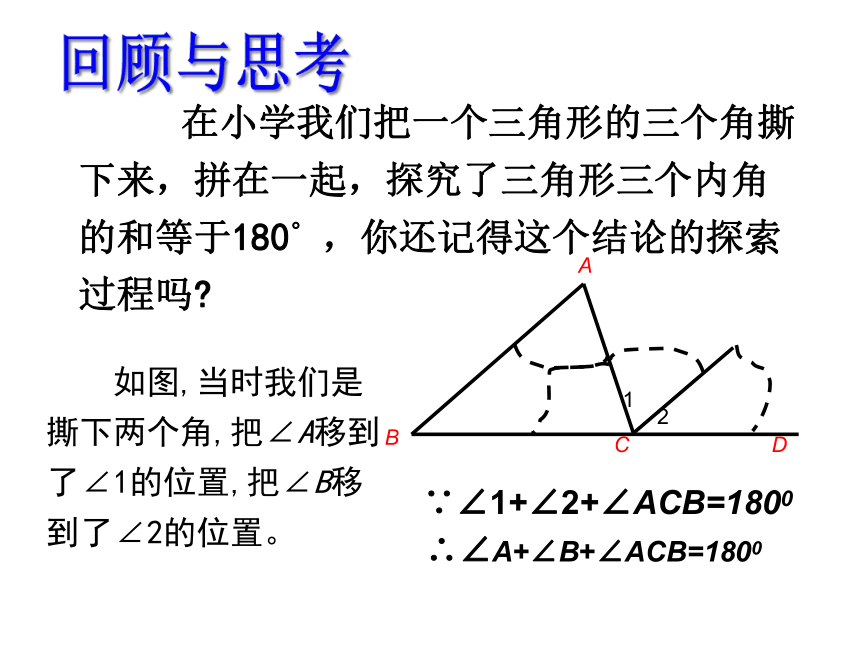
在小学我们把一个三角形的三个角撕下来,拼在一起,探究了三角形三个内角的和等于180? ,你还记得这个结论的探索过程吗?
1
A
B
D
2
C
如图,当时我们是撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置。
∵∠1+∠2+∠ACB=1800
∴∠A+∠B+∠ACB=1800
如果只撕下一个角,你能用学过的知识拼凑并解释“三角形的三个内角和是180?”吗?
1
2
3
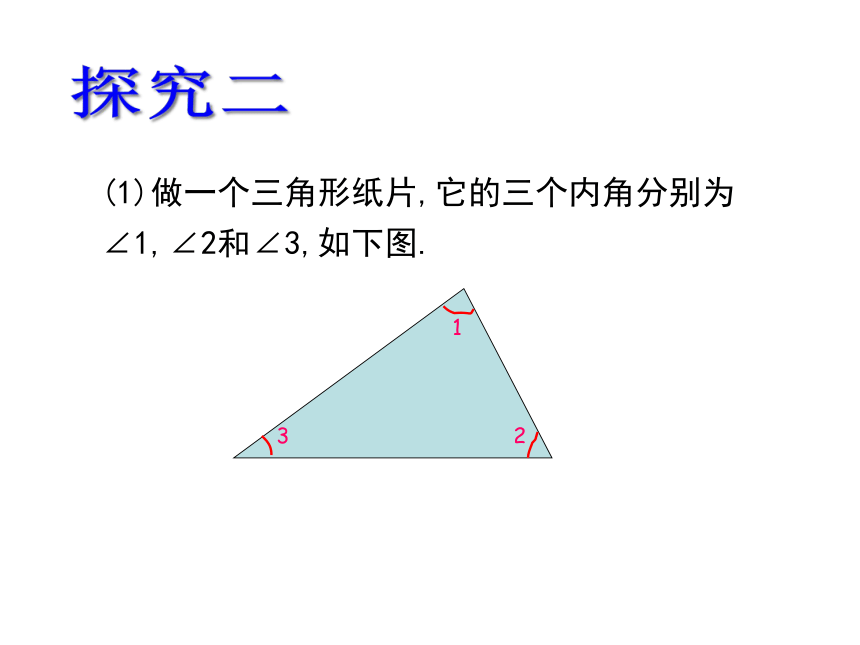
(1)做一个三角形纸片,它的三个内角分别为∠1,∠2和∠3,如下图.
1
2
3
(2)将∠1撕下,并按下图进行摆放,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合.此时∠1的另一条边b与∠3的一条边a 平行吗?为什么?
1
a
b
1
1
2
3
1
a
b
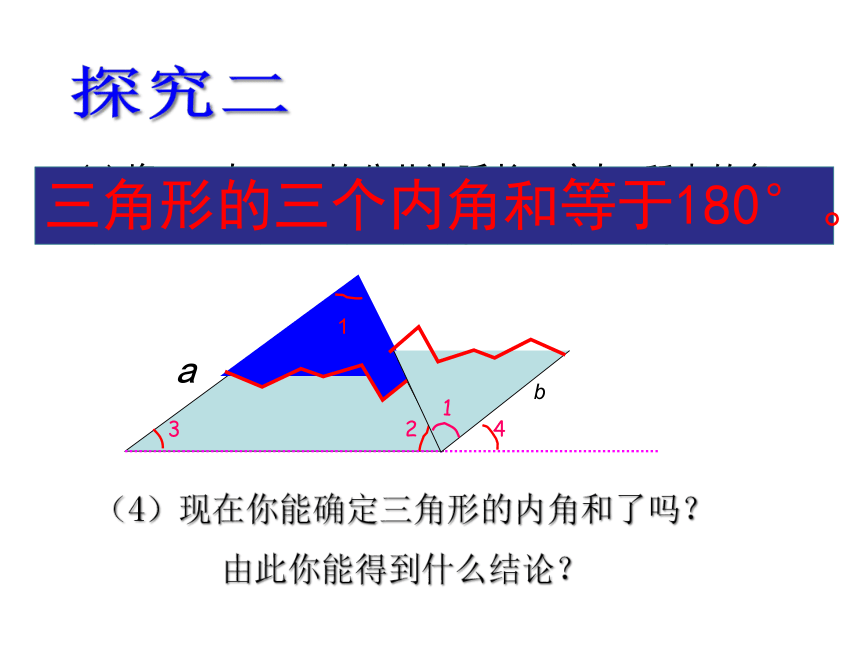
(3)将∠2与∠3的公共边延长,它与b所夹的角为∠4. ∠3与∠4的大小有什么关系?为什么?
4
(4)现在你能确定三角形的内角和了吗?
由此你能得到什么结论?
三角形的三个内角和等于180°。
1
(1)图4-7小明所拿的三角形被遮住的两个内角是什么角?小颖的呢?试着说明理由。
(2)图4-8中三角形被遮住的两个内角可能是什么角?将所得的结果与(1)的结果进行比较,可以将三角形如何按角分类?
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
直角边
直角边
斜边
1.常用符号“Rt?ABC”来表示,
读作直角三角形ABC.
2.直角三角形的两个锐角之间
有什么关系?
直角三角形的两个锐角互余
A
B
C
观察下图中的三角形,你能够按角将
它们的形状分类吗?
(1)(5)是锐角三角形
想一想
(3)是直角三角形
(2)(4)是钝角三角形
2.一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30度和60度
(2)40度和70度
(3)50度和20度
直角三角形
锐角三角形
钝角三角形
请你谈一谈:
通过这节课的学习,你对三角形又多了哪些认识?
1.三角形三个内角的和等于180 ? .
2.三角形按角的大小分类:
⑴锐角三角形 :三个内角都是锐角;
⑵直角三角形 :有一个内角为直角;
⑶钝角三角形 :有一个内角为钝角 。
3.直角三角形的两个锐角互余。
提高篇
5分
8分
基础篇
4分
4分
2分
3分
你争我抢
作业: 1.助学第一课时;
2.以三角形为主图形,自制一张
卡片,设计自己喜欢的图案送给妈妈 .
如果△ABC中,∠A∶∠B∶∠C=2∶3∶5,则∠A=( )∠B=( ),∠C=( ),此三角形按角分类应为( ) 三角形。
36°
54°
90°
直角
1.在下面的空白处,分别填入“锐角”,“钝角”
或“直角”:
(1)如果三角形的三个内角都相等,那么这个三角形是 三角形;
(2)如果三角形的一个内角等于另外两个 内角之和,那么这个三角形是 三角形;
(3)如果三角形的两个内角都小于40度,那么这个三角形是 三角形.
钝角
锐角
直角
指出图中有_____个三角形,它们分别是_____________________________。
B
A
D
C
E
4
△ABD △DCE △DCB △ECB
聪明的你能写出图中所有的三角形吗?
△ABD △ABE △ABC
小思考:1.∠B的对边:
2.以AD为边的三角形有:
AD , AE , AC
△ABD △ADE △ADC
B
A
C
D
E
△ADE △ADC
△AEC
已知∠ACB=90°,CD⊥AB,垂足为D.
C
B
A
D
2
Rt?ACB
Rt?ADC
Rt?BDC
1
⑴ 图中有几个直角三角形?是哪几个?
⑵ ∠2和∠A有什么关系?∠1和∠A呢?为什么?
证明:在Rt?ADC中,∠ADC =90°
又∵ ∠2+∠1= 90°
∴ ∠1=∠A(同角的余角相等。)
解: ∠2和∠A互余 ∠1和∠A相等
∴ ∠2+∠A =90°
(直角三角形的两个锐角互余。)
如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,轮船行驶到哪一点时距离灯塔最近?当轮船从A点行驶到B点时,∠ACB的度数是多少?当轮船距离灯塔C最近点时呢?
400
600
证法2:
)
1
2
C
A
E
)
B
D
过C作CE∥BA.
作BC的延长线CD,
∵CE∥BA
∴∠A=∠1(两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(等量代换)
C
A
B
E
F
证法3:
过A作EF∥BC
观察房屋顶的框架
⑴ 你能从图中找出4个不同的三角形吗?
(2)与同伴交流各自找到的三角形.
(3)这些三角形有什么共同的特点?
斜梁
斜梁
直 梁
证明:
在△ABC的外部,以点C为顶点,CA为一边,
作∠1=∠A,
作BC的延长线CD,
∵∠1=∠A
∴CE∥BA(内错角相等,两直线平行)
∴∠B=∠2
(两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(等量代换)
)
1
2
C
A
E
)
B
D
边:
顶点A所对的边BC可表示为: a
角:
顶点:
∠A ∠B ∠C
顶点A B C
边:
b
a
三边AB BC AC
记法:
三角形符号“△”
记作:△ABC (△BCA或 △CBA )
顶点B所对的边AC可表示为:
顶点C所对的边AB可表示为:
b
c
读作“三角形ABC”
c
A
B
C
三角形的概念
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2
3
4
北师大七年级下册
学习目标:
1、通过观察、推理、交流等活动,发展空间观念、推理能力和有条理的表达能力。
2、?结合实例进一步认识三角形的概念及基本要素,能用符号语言表示三角形;?探究发现三角形内角和等于180°;?能按三角形内角大小进行分类。④能用运用直角三角形两锐角互余的性质解决简单的问题。
3、树立几何知识源于客观实际,用于客观实际的观念,激发学习兴趣。
A
D
B
E
C
找一找
按照老师的提示找出图中有哪几个三角形
在小学我们把一个三角形的三个角撕下来,拼在一起,探究了三角形三个内角的和等于180? ,你还记得这个结论的探索过程吗?
1
A
B
D
2
C
如图,当时我们是撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置。
∵∠1+∠2+∠ACB=1800
∴∠A+∠B+∠ACB=1800
如果只撕下一个角,你能用学过的知识拼凑并解释“三角形的三个内角和是180?”吗?
1
2
3
(1)做一个三角形纸片,它的三个内角分别为∠1,∠2和∠3,如下图.
1
2
3
(2)将∠1撕下,并按下图进行摆放,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合.此时∠1的另一条边b与∠3的一条边a 平行吗?为什么?
1
a
b
1
1
2
3
1
a
b
(3)将∠2与∠3的公共边延长,它与b所夹的角为∠4. ∠3与∠4的大小有什么关系?为什么?
4
(4)现在你能确定三角形的内角和了吗?
由此你能得到什么结论?
三角形的三个内角和等于180°。
1
(1)图4-7小明所拿的三角形被遮住的两个内角是什么角?小颖的呢?试着说明理由。
(2)图4-8中三角形被遮住的两个内角可能是什么角?将所得的结果与(1)的结果进行比较,可以将三角形如何按角分类?
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
直角边
直角边
斜边
1.常用符号“Rt?ABC”来表示,
读作直角三角形ABC.
2.直角三角形的两个锐角之间
有什么关系?
直角三角形的两个锐角互余
A
B
C
观察下图中的三角形,你能够按角将
它们的形状分类吗?
(1)(5)是锐角三角形
想一想
(3)是直角三角形
(2)(4)是钝角三角形
2.一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30度和60度
(2)40度和70度
(3)50度和20度
直角三角形
锐角三角形
钝角三角形
请你谈一谈:
通过这节课的学习,你对三角形又多了哪些认识?
1.三角形三个内角的和等于180 ? .
2.三角形按角的大小分类:
⑴锐角三角形 :三个内角都是锐角;
⑵直角三角形 :有一个内角为直角;
⑶钝角三角形 :有一个内角为钝角 。
3.直角三角形的两个锐角互余。
提高篇
5分
8分
基础篇
4分
4分
2分
3分
你争我抢
作业: 1.助学第一课时;
2.以三角形为主图形,自制一张
卡片,设计自己喜欢的图案送给妈妈 .
如果△ABC中,∠A∶∠B∶∠C=2∶3∶5,则∠A=( )∠B=( ),∠C=( ),此三角形按角分类应为( ) 三角形。
36°
54°
90°
直角
1.在下面的空白处,分别填入“锐角”,“钝角”
或“直角”:
(1)如果三角形的三个内角都相等,那么这个三角形是 三角形;
(2)如果三角形的一个内角等于另外两个 内角之和,那么这个三角形是 三角形;
(3)如果三角形的两个内角都小于40度,那么这个三角形是 三角形.
钝角
锐角
直角
指出图中有_____个三角形,它们分别是_____________________________。
B
A
D
C
E
4
△ABD △DCE △DCB △ECB
聪明的你能写出图中所有的三角形吗?
△ABD △ABE △ABC
小思考:1.∠B的对边:
2.以AD为边的三角形有:
AD , AE , AC
△ABD △ADE △ADC
B
A
C
D
E
△ADE △ADC
△AEC
已知∠ACB=90°,CD⊥AB,垂足为D.
C
B
A
D
2
Rt?ACB
Rt?ADC
Rt?BDC
1
⑴ 图中有几个直角三角形?是哪几个?
⑵ ∠2和∠A有什么关系?∠1和∠A呢?为什么?
证明:在Rt?ADC中,∠ADC =90°
又∵ ∠2+∠1= 90°
∴ ∠1=∠A(同角的余角相等。)
解: ∠2和∠A互余 ∠1和∠A相等
∴ ∠2+∠A =90°
(直角三角形的两个锐角互余。)
如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,轮船行驶到哪一点时距离灯塔最近?当轮船从A点行驶到B点时,∠ACB的度数是多少?当轮船距离灯塔C最近点时呢?
400
600
证法2:
)
1
2
C
A
E
)
B
D
过C作CE∥BA.
作BC的延长线CD,
∵CE∥BA
∴∠A=∠1(两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(等量代换)
C
A
B
E
F
证法3:
过A作EF∥BC
观察房屋顶的框架
⑴ 你能从图中找出4个不同的三角形吗?
(2)与同伴交流各自找到的三角形.
(3)这些三角形有什么共同的特点?
斜梁
斜梁
直 梁
证明:
在△ABC的外部,以点C为顶点,CA为一边,
作∠1=∠A,
作BC的延长线CD,
∵∠1=∠A
∴CE∥BA(内错角相等,两直线平行)
∴∠B=∠2
(两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(等量代换)
)
1
2
C
A
E
)
B
D
边:
顶点A所对的边BC可表示为: a
角:
顶点:
∠A ∠B ∠C
顶点A B C
边:
b
a
三边AB BC AC
记法:
三角形符号“△”
记作:△ABC (△BCA或 △CBA )
顶点B所对的边AC可表示为:
顶点C所对的边AB可表示为:
b
c
读作“三角形ABC”
c
A
B
C
三角形的概念
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
