第15章分式(小结复习课时1)-人教版八年级数学上册课件(共24张ppt)
文档属性
| 名称 | 第15章分式(小结复习课时1)-人教版八年级数学上册课件(共24张ppt) | 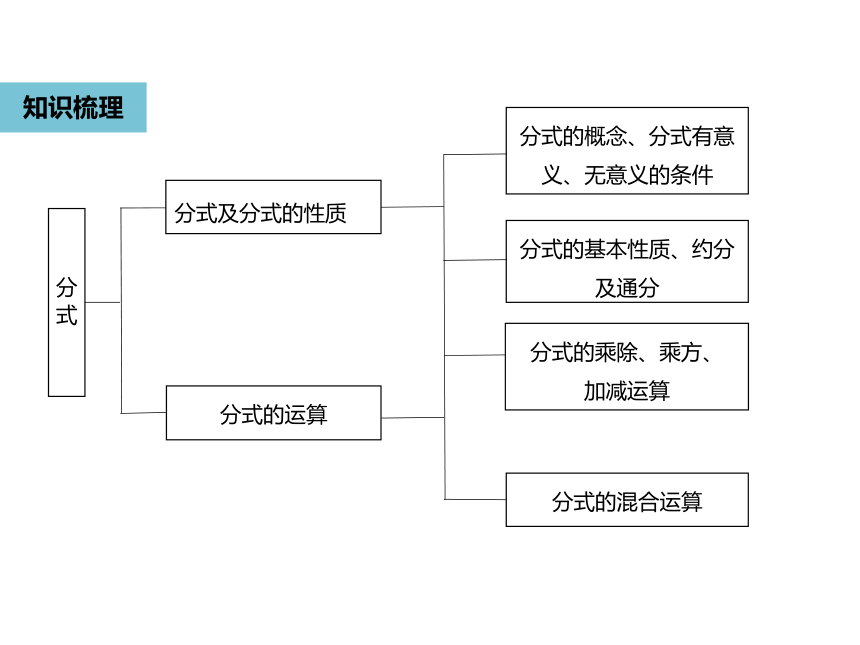 | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 19:42:04 | ||
图片预览









文档简介
知识梳理
分式
分式及分式的性质
分式的运算
分式的概念、分式有意义、无意义的条件
分式的基本性质、约分
及通分
分式的乘除、乘方、
加减运算
分式的混合运算
知识梳理
分式:一般地,如果A、B表示两个整式,并且B中含有字母,那么式子 叫做分式. 分式 中,A叫做分子,B叫做分母.
分式必须满足三个条件:①形如 的式子;②A、B都是整式;③分母B中含有字母. 三个条件缺一不可.
判断一个式子是否为分式,不能将其化简后再判断,只需看原式的本来“面目”是否符合分式的概念.
知识梳理
分式有意义的条件:分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式 才有意义.
分式的值为0的条件:当分式的分子等于0且分母不等于0时,分式的值为0.
分式无意义的条件:分式的分母为0,即当B=0时,分式 无意义.
知识梳理
基本性质
分式的分子与分母乘(或除以)同一个不为0的整式,分式的值不变.
式子表示
, (C≠0),其中A,B,C是整式.
注意事项
(1)分子和分母同时做“乘法(或除法)”运算;
(2)乘(或除以)的对象必须是同一个不等于0的整式.
用途
进行分式的恒等变形
分式的基本性质
知识梳理
分式的符号法则:分式的分子、分母与分式本身这三处的正负号,同时改变两处,分式的值不变.
用式子表示:
当分式的分子、分母是多项式时,不要把分子或分母第一项的符号误认为是分子或分母的符号.
知识梳理
分式的约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.
最简分式:分子与分母没有公因式的分式,叫做最简分式.
约分不改变分式的值,但可能改变分式中字母的取值范围,因此在确定分式中字母的范围时,不能进行约分.
知识梳理
分式的通分:根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分.
最简公分母:通分时,一般取各分母的所有因式的最高次幂的积作为公分母,这样的分母叫做最简公分母.
在确定几个分式的最简公分母时,不要遗漏只在一个分式的分母中出现的字母及其指数.
知识梳理
用式子表示:
分式的乘法法则:分式乘以分式,用分子的积作为积的分子,分母的积作为积的分母.
用式子表示:
分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
知识梳理
分式的乘方法则:分式的乘方要把分子、分母分别乘方.
用式子表示: (n为正整数).
a,b分别表示分子与分母,它们可以是单项式,也可以是多项式.
知识梳理
同分母分式的加减法法则:同分母分式相加减,分母不变,把分子相加减.
用式子表示:
异分母分式的加减法法则:异分母分式相加减,先通分,变为同分母的分式,再加减.
用式子表示:
知识梳理
分式的混合运算顺序:先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
分式的混合运算中要注意各分式中分子、分母符号的处理,结果中分子或分母的系数(或首项的系数)是负数时,要把“-”号提到分式本身的前面.
知识梳理
负整数指数幂的三个常用结论:
(1)an与a-n互为倒数;
负整数指数幂:一般地,当n是正整数时, (a≠0).这就是说 (a≠0)是 的倒数.
(3) .
当指数为负整数或 0 时,一定要保证底数不为 0 .
(2) ;
知识梳理
用科学记数法表示小于1的正数:小于1的正数可以用科学记数法表示为a×10-n的形式,其中1≤a<10,n是正整数.
科学记数法是一种记数方法,不改变此数的性质和大小,用科学记数法表示一个负数时,不要忘了前面带“-”号,用科学记数法表示一个带有单位的数时,其表示结果也应带有单位.
重点解析
1
(1)分式 有意义的条件是____________,值为零的条件是_______.
(2)分式 无意义的条件是___________,值为零的条件是________.
x≠1且x≠2
x=±3
x=-2
x=0
重点解析
2
下列等式从左到右变形一定正确的是( )
C
A. B.
C. D.
解析:根据分式的基本性质可知A、B选项错误;
选项C是分子、分母同时除以c,c在左边的分子、分母中,说明c不为0;
选项D是分子、分母同时乘c,但是没有说明c是否为0.
重点解析
3
计算:
解:(1)原式
本题源自《教材帮》
(1) (2)
重点解析
3
计算:
本题源自《教材帮》
解:(2)原式
(1) (2)
重点解析
4
计算:
本题源自《教材帮》
解:(1)原式
(1) (2)
重点解析
4
计算:
本题源自《教材帮》
解:(2)原式
(1) (2)
重点解析
5
用科学记数法表示下列各数:
(1)0.00001 (2)0.000000567
(3)0.000000301 (4)-0.0023
解:(1)0.00001=1×10-5
(2)0.000000567=5.67×10-7
(3)0.000000301=3.01×10-7
(4)-0.0023=-2.3×10-3
深化练习
1
计算:
(1) (2)
解:(1)原式
深化练习
1
计算:
解:(2)原式
(1) (2)
深化练习
2
本题源自《教材帮》
解:原式
先化简,再求值: ,其中x的值从不等式组
2-x≤3
2x-4<1 的整数解中选取.
深化练习
2
本题源自《教材帮》
先化简,再求值: ,其中x的值从不等式组
2-x≤3
2x-4<1 的整数解中选取.
解:解不等式组得: .
则不等式组的整数解有-1、0、1、2
当x=1、-1、0时,原分式无意义.
所以x=2,原式=0.
注意:代入原分式的值必须使原分式有意义.
分式
分式及分式的性质
分式的运算
分式的概念、分式有意义、无意义的条件
分式的基本性质、约分
及通分
分式的乘除、乘方、
加减运算
分式的混合运算
知识梳理
分式:一般地,如果A、B表示两个整式,并且B中含有字母,那么式子 叫做分式. 分式 中,A叫做分子,B叫做分母.
分式必须满足三个条件:①形如 的式子;②A、B都是整式;③分母B中含有字母. 三个条件缺一不可.
判断一个式子是否为分式,不能将其化简后再判断,只需看原式的本来“面目”是否符合分式的概念.
知识梳理
分式有意义的条件:分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式 才有意义.
分式的值为0的条件:当分式的分子等于0且分母不等于0时,分式的值为0.
分式无意义的条件:分式的分母为0,即当B=0时,分式 无意义.
知识梳理
基本性质
分式的分子与分母乘(或除以)同一个不为0的整式,分式的值不变.
式子表示
, (C≠0),其中A,B,C是整式.
注意事项
(1)分子和分母同时做“乘法(或除法)”运算;
(2)乘(或除以)的对象必须是同一个不等于0的整式.
用途
进行分式的恒等变形
分式的基本性质
知识梳理
分式的符号法则:分式的分子、分母与分式本身这三处的正负号,同时改变两处,分式的值不变.
用式子表示:
当分式的分子、分母是多项式时,不要把分子或分母第一项的符号误认为是分子或分母的符号.
知识梳理
分式的约分:根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.
最简分式:分子与分母没有公因式的分式,叫做最简分式.
约分不改变分式的值,但可能改变分式中字母的取值范围,因此在确定分式中字母的范围时,不能进行约分.
知识梳理
分式的通分:根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分.
最简公分母:通分时,一般取各分母的所有因式的最高次幂的积作为公分母,这样的分母叫做最简公分母.
在确定几个分式的最简公分母时,不要遗漏只在一个分式的分母中出现的字母及其指数.
知识梳理
用式子表示:
分式的乘法法则:分式乘以分式,用分子的积作为积的分子,分母的积作为积的分母.
用式子表示:
分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
知识梳理
分式的乘方法则:分式的乘方要把分子、分母分别乘方.
用式子表示: (n为正整数).
a,b分别表示分子与分母,它们可以是单项式,也可以是多项式.
知识梳理
同分母分式的加减法法则:同分母分式相加减,分母不变,把分子相加减.
用式子表示:
异分母分式的加减法法则:异分母分式相加减,先通分,变为同分母的分式,再加减.
用式子表示:
知识梳理
分式的混合运算顺序:先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
分式的混合运算中要注意各分式中分子、分母符号的处理,结果中分子或分母的系数(或首项的系数)是负数时,要把“-”号提到分式本身的前面.
知识梳理
负整数指数幂的三个常用结论:
(1)an与a-n互为倒数;
负整数指数幂:一般地,当n是正整数时, (a≠0).这就是说 (a≠0)是 的倒数.
(3) .
当指数为负整数或 0 时,一定要保证底数不为 0 .
(2) ;
知识梳理
用科学记数法表示小于1的正数:小于1的正数可以用科学记数法表示为a×10-n的形式,其中1≤a<10,n是正整数.
科学记数法是一种记数方法,不改变此数的性质和大小,用科学记数法表示一个负数时,不要忘了前面带“-”号,用科学记数法表示一个带有单位的数时,其表示结果也应带有单位.
重点解析
1
(1)分式 有意义的条件是____________,值为零的条件是_______.
(2)分式 无意义的条件是___________,值为零的条件是________.
x≠1且x≠2
x=±3
x=-2
x=0
重点解析
2
下列等式从左到右变形一定正确的是( )
C
A. B.
C. D.
解析:根据分式的基本性质可知A、B选项错误;
选项C是分子、分母同时除以c,c在左边的分子、分母中,说明c不为0;
选项D是分子、分母同时乘c,但是没有说明c是否为0.
重点解析
3
计算:
解:(1)原式
本题源自《教材帮》
(1) (2)
重点解析
3
计算:
本题源自《教材帮》
解:(2)原式
(1) (2)
重点解析
4
计算:
本题源自《教材帮》
解:(1)原式
(1) (2)
重点解析
4
计算:
本题源自《教材帮》
解:(2)原式
(1) (2)
重点解析
5
用科学记数法表示下列各数:
(1)0.00001 (2)0.000000567
(3)0.000000301 (4)-0.0023
解:(1)0.00001=1×10-5
(2)0.000000567=5.67×10-7
(3)0.000000301=3.01×10-7
(4)-0.0023=-2.3×10-3
深化练习
1
计算:
(1) (2)
解:(1)原式
深化练习
1
计算:
解:(2)原式
(1) (2)
深化练习
2
本题源自《教材帮》
解:原式
先化简,再求值: ,其中x的值从不等式组
2-x≤3
2x-4<1 的整数解中选取.
深化练习
2
本题源自《教材帮》
先化简,再求值: ,其中x的值从不等式组
2-x≤3
2x-4<1 的整数解中选取.
解:解不等式组得: .
则不等式组的整数解有-1、0、1、2
当x=1、-1、0时,原分式无意义.
所以x=2,原式=0.
注意:代入原分式的值必须使原分式有意义.
