华东师大版九年级下册数学课件:26.2.1二次函数y=ax2的图象和性质(共23 张ppt)
文档属性
| 名称 | 华东师大版九年级下册数学课件:26.2.1二次函数y=ax2的图象和性质(共23 张ppt) | 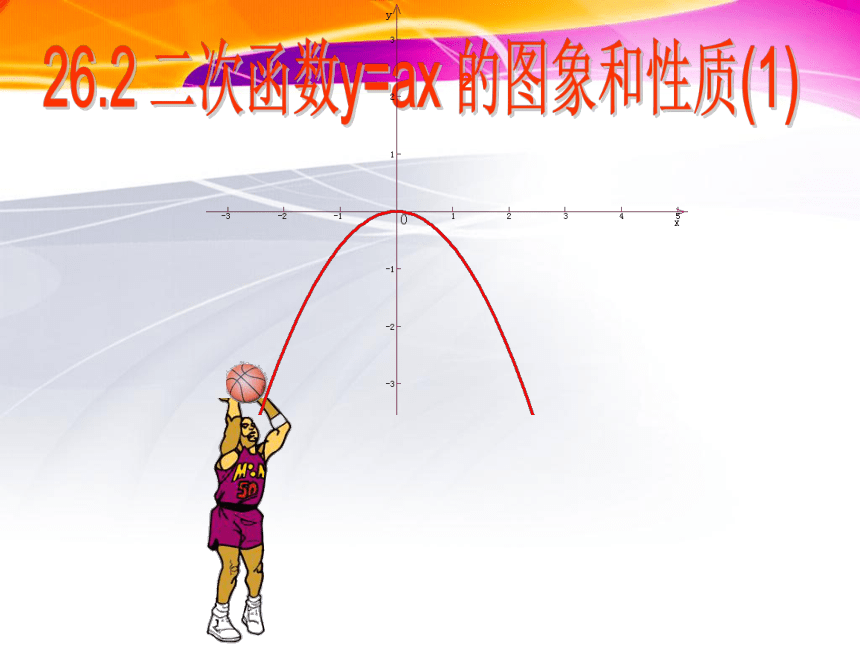 | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 19:52:01 | ||
图片预览






文档简介
2
1、二次函数的一般形式是怎样的?
y=ax?+bx+c(a,b,c是常数,a≠ 0)
2.下列函数中,哪些是二次函数?
①
⑤
④
③
②
③
在下列函数中①y=2x ②y=-3x-2
1、它们的图像分别是什么样子?
在下列函数中①y=2x ②y=-3x-2
在下列函数中①y=2x ②y=-3x-2
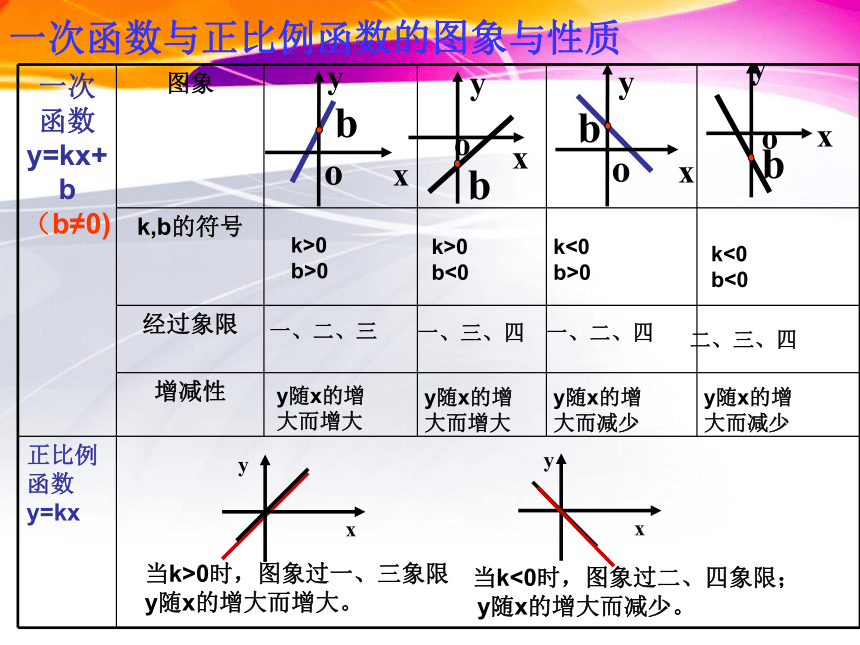
一次函数与正比例函数的图象与性质
一次函数y=kx+b(b≠0)
图象
k,b的符号
经过象限
增减性
正比例函数y=kx
x
y
o
b
x
y
o
b
x
y
o
b
x
y
o
b
k>0
b>0
一、二、三
y随x的增
大而增大
k>0
b<0
一、三、四
y随x的增
大而增大
k<0
b>0
一、二、四
y随x的增
大而减少
k<0
b<0
二、三、四
y随x的增
大而减少
当k<0时,图象过二、四象限;
y随x的增大而减少。
x
y
x
y
当k>0时,图象过一、三象限
y随x的增大而增大。
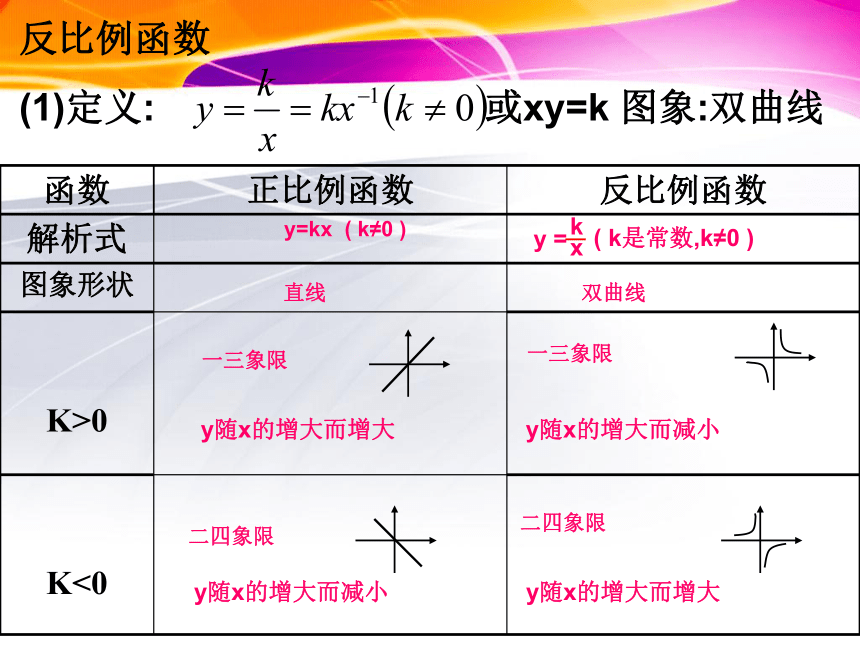
反比例函数
(1)定义: 或xy=k 图象:双曲线
函数
正比例函数
反比例函数
解析式
图象形状
K>0
K<0
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
y随x的增大而减小
y随x的增大而增大
二四象限
你知道吗?
二次函数y=
的图像是什么样子呢?
猜一猜
画函数图像的一般步骤是:
列表、描点、连线 、写解析式。
我想知道二次函数的图像是否也为直线或双曲线,我该怎么解决这一问题呢?
1、画函数图像
2、如何画函数图像 呢?
学习目标一
探索二次函数 , 的图像与性质。
做一做:二次函数 的图像
X的值可以取哪些呢?
x
…
-3
-2
-1
0
1
2
3
…
y
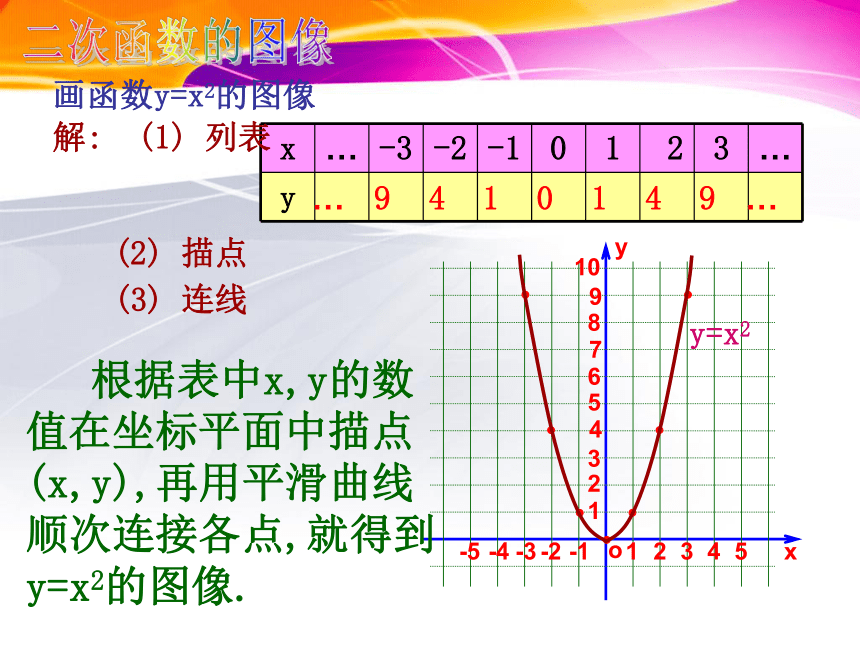
画函数y=x2的图像
解: (1) 列表
…
9
4
1
0
1
4
9
…
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=x2的图像.
y=x2
x
…
-3
-2
-1
0
1
2
3
…
y
请画函数y=-x2的图像
解: (1) 列表
…
-9
-4
-1
0
-1
4
-9
…
(2) 描点
(3) 连线
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=x2的图像.
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
y=-x2
x
y
o
x
y
o
从图像可以看出,二次函数y=x2和y=-x2的图像都是一条曲线,它的形状类似于投篮球或投掷铅球时球在空中所经过的路线.
这样的曲线叫做抛物线.
y=x2的图像叫做抛物线y=x2.
y=-x2的图像叫做抛物线y=-x2.
实际上,二次函数的图像都是抛物线.
它们的开口向上或者向下.
一般地,二次函数y=ax2+bx+c 的图像叫做抛物线y=ax2+bx+c.
还可以看出,二次函数y=x2和y=-x2的图像都是轴对称图形,y轴是它们的对称轴.
抛物线与对称轴的交点叫做抛物线的顶点.
抛物线y=x2的顶点(0,0)是它的最低点.
抛物线y=-x2的顶点(0,0)是它的最高点.
y=x2
y=-x2
二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
x
…
-4
-3
-2
-1
0
1
2
3
4
…
y= x2
例1.在同一直角坐标系中画出函数y= x2和y=2x2的图像
解: (1) 列表
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
1
2
x
…
-2
1.5
-1
0.5
0
0.5
1
1.5
2
…
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
1
2
函数y= x2,y=2x2的图像与函数y=x2(图中虚线图形)的图像相比,有什么共同点和不同点?
1
2
共同点:
不同点:
开口向上;
除顶点外,图像都在x轴上方
开口大小不同;
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x
…
-4
-3
-2
-1
0
1
2
3
4
…
在同一直角坐标系中画出函数y=- x2和y=-2x2的图像
解: (1) 列表
(2) 描点
(3) 连线
1
2
x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…
y=-2x2
-8
…
-2
-0.5
0
-0.5
-2
-4.5
-8
…
-4.5
-8
…
-2
-0.5
0
-0.5
-2
-4.5
-8
…
-4.5
函数y=- x2,y=-2x2的图像与函数y=-x2(图中虚线图形)的图像相比,有什么共同点和不同点?
1
2
共同点:
不同点:
开口向下;
除顶点外,图像都在x轴下方
开口大小不同;
1
2
y=- x2
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
一般地,抛物线y=ax2的顶点是原点.对称轴是y轴
当a>0时,抛物线的开口向上,顶点是抛物线的最低点,
a越大,抛物线的开口越小;
当a<0时,抛物线的开口向上,顶点是抛物线的最高点,
a越大,抛物线的开口越大;
在同一坐标系内,抛物线y=ax2与抛物线y=-ax2是关于x轴对称的.
a>0
a<0
当a>0时,在对称轴的
左侧,y随着x的增大而
减小。
当a>0时,在对称轴的
右侧,y随着x的增大而
增大。
当a<0时,在对称轴的
左侧,y随着x的增大而
增大。
当a<0时,在对称轴的
右侧,y随着x的增大而
减小。
当x=-2时,y=4
当x=-1时,y=1
当x=1时,y=1
当x=2时,y=4
当x=-2时,y=-4
当x=-1时,y=-1
当x=1时,y=-1
当x=2时,y=-4
抛物线y=x2在x轴的
上方(除顶点外),顶点
是它的最低点,开口
向上,并且向上无限
伸展;当x=0时,函数y
的值最小,最小值是0.
抛物线y=-x2在x轴的
下方(除顶点外),顶点
是它的最高点,开口
向下,并且向下无限
伸展;当x=0时,函数y
的值最大,最大值是0.
1、根据左边已画好的函数图象填空:
(1)抛物线y=2x2的顶点坐标是 ,
对称轴是 ,在 侧,
y随着x的增大而增大;在 侧,
y随着x的增大而减小,当x= 时,
函数y的值最小,最小值是 ,抛物
线y=2x2在x轴的 方(除顶点外)。
(2)抛物线 在x轴的 方(除顶点外),在对称轴的
左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
(0,0)
y轴
对称轴的右
对称轴的左
0
0
上
下
增大而增大
增大而减小
0
2
二次函数y=ax2的性质
1.顶点坐标及最高点、最低点与对称轴
2.位置及延伸的方向与开口方向
3.最值与增减性
在y轴左右两侧同时向上无限延伸
在y轴左右两侧同时向下无限延伸
开口大小
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2 (a>0)
y= ax2 (a<0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
|a|越小,开口越大.
|a|越大,开口越小.
(0,0)
最低点
最高点
4.开口大小
1、函数y=2x2的图象的开口 ,对称轴 ,顶点是 ;
2、函数y=-3x2的图象的开口 ,对称轴 ,顶点是 ;
向上
向下
y轴
y轴
(0,0)
(0,0)
做一做
(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,
在对称轴 侧,y随着x的增大而增大;在对称轴 侧,
y随着x的增大而减小,当x= 时,函数y的值最小,最小
值是 ,抛物线y=2x2在x轴的 方(除顶点外).
(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
例3.已知 y =(m+1)x 是二次函数且其图象开口向上,求m的值和函数解析式
m2+m
解: 依题意有:
m+1>0 ①
m2+m=2 ②
解②得:m1=-2, m2=1
由①得:m>-1
∴ m=1
此时,二次函数为: y=2x2,
知道就做别客气
当堂检测
3.若二次函数 是开口向上的抛物线,则k的值是( )
A. -3 B. 2 C. 3 D.-3或2
B
4.已知 是二次函数y=x2图象上的一点,则图象上与之对称的点的坐标是( )
A. B. C. D.
5.已知a﹤-1,A(a-1,y1),B(a,y2)C(a+1,y3)
为二次函数y=x2的图象上的三点,则y1,y2,y3的大小关系是( )
B.
D.
B
B
1、二次函数的一般形式是怎样的?
y=ax?+bx+c(a,b,c是常数,a≠ 0)
2.下列函数中,哪些是二次函数?
①
⑤
④
③
②
③
在下列函数中①y=2x ②y=-3x-2
1、它们的图像分别是什么样子?
在下列函数中①y=2x ②y=-3x-2
在下列函数中①y=2x ②y=-3x-2
一次函数与正比例函数的图象与性质
一次函数y=kx+b(b≠0)
图象
k,b的符号
经过象限
增减性
正比例函数y=kx
x
y
o
b
x
y
o
b
x
y
o
b
x
y
o
b
k>0
b>0
一、二、三
y随x的增
大而增大
k>0
b<0
一、三、四
y随x的增
大而增大
k<0
b>0
一、二、四
y随x的增
大而减少
k<0
b<0
二、三、四
y随x的增
大而减少
当k<0时,图象过二、四象限;
y随x的增大而减少。
x
y
x
y
当k>0时,图象过一、三象限
y随x的增大而增大。
反比例函数
(1)定义: 或xy=k 图象:双曲线
函数
正比例函数
反比例函数
解析式
图象形状
K>0
K<0
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
y随x的增大而减小
y随x的增大而增大
二四象限
你知道吗?
二次函数y=
的图像是什么样子呢?
猜一猜
画函数图像的一般步骤是:
列表、描点、连线 、写解析式。
我想知道二次函数的图像是否也为直线或双曲线,我该怎么解决这一问题呢?
1、画函数图像
2、如何画函数图像 呢?
学习目标一
探索二次函数 , 的图像与性质。
做一做:二次函数 的图像
X的值可以取哪些呢?
x
…
-3
-2
-1
0
1
2
3
…
y
画函数y=x2的图像
解: (1) 列表
…
9
4
1
0
1
4
9
…
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=x2的图像.
y=x2
x
…
-3
-2
-1
0
1
2
3
…
y
请画函数y=-x2的图像
解: (1) 列表
…
-9
-4
-1
0
-1
4
-9
…
(2) 描点
(3) 连线
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=x2的图像.
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
y=-x2
x
y
o
x
y
o
从图像可以看出,二次函数y=x2和y=-x2的图像都是一条曲线,它的形状类似于投篮球或投掷铅球时球在空中所经过的路线.
这样的曲线叫做抛物线.
y=x2的图像叫做抛物线y=x2.
y=-x2的图像叫做抛物线y=-x2.
实际上,二次函数的图像都是抛物线.
它们的开口向上或者向下.
一般地,二次函数y=ax2+bx+c 的图像叫做抛物线y=ax2+bx+c.
还可以看出,二次函数y=x2和y=-x2的图像都是轴对称图形,y轴是它们的对称轴.
抛物线与对称轴的交点叫做抛物线的顶点.
抛物线y=x2的顶点(0,0)是它的最低点.
抛物线y=-x2的顶点(0,0)是它的最高点.
y=x2
y=-x2
二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
x
…
-4
-3
-2
-1
0
1
2
3
4
…
y= x2
例1.在同一直角坐标系中画出函数y= x2和y=2x2的图像
解: (1) 列表
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
1
2
x
…
-2
1.5
-1
0.5
0
0.5
1
1.5
2
…
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
1
2
函数y= x2,y=2x2的图像与函数y=x2(图中虚线图形)的图像相比,有什么共同点和不同点?
1
2
共同点:
不同点:
开口向上;
除顶点外,图像都在x轴上方
开口大小不同;
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x
…
-4
-3
-2
-1
0
1
2
3
4
…
在同一直角坐标系中画出函数y=- x2和y=-2x2的图像
解: (1) 列表
(2) 描点
(3) 连线
1
2
x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…
y=-2x2
-8
…
-2
-0.5
0
-0.5
-2
-4.5
-8
…
-4.5
-8
…
-2
-0.5
0
-0.5
-2
-4.5
-8
…
-4.5
函数y=- x2,y=-2x2的图像与函数y=-x2(图中虚线图形)的图像相比,有什么共同点和不同点?
1
2
共同点:
不同点:
开口向下;
除顶点外,图像都在x轴下方
开口大小不同;
1
2
y=- x2
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
一般地,抛物线y=ax2的顶点是原点.对称轴是y轴
当a>0时,抛物线的开口向上,顶点是抛物线的最低点,
a越大,抛物线的开口越小;
当a<0时,抛物线的开口向上,顶点是抛物线的最高点,
a越大,抛物线的开口越大;
在同一坐标系内,抛物线y=ax2与抛物线y=-ax2是关于x轴对称的.
a>0
a<0
当a>0时,在对称轴的
左侧,y随着x的增大而
减小。
当a>0时,在对称轴的
右侧,y随着x的增大而
增大。
当a<0时,在对称轴的
左侧,y随着x的增大而
增大。
当a<0时,在对称轴的
右侧,y随着x的增大而
减小。
当x=-2时,y=4
当x=-1时,y=1
当x=1时,y=1
当x=2时,y=4
当x=-2时,y=-4
当x=-1时,y=-1
当x=1时,y=-1
当x=2时,y=-4
抛物线y=x2在x轴的
上方(除顶点外),顶点
是它的最低点,开口
向上,并且向上无限
伸展;当x=0时,函数y
的值最小,最小值是0.
抛物线y=-x2在x轴的
下方(除顶点外),顶点
是它的最高点,开口
向下,并且向下无限
伸展;当x=0时,函数y
的值最大,最大值是0.
1、根据左边已画好的函数图象填空:
(1)抛物线y=2x2的顶点坐标是 ,
对称轴是 ,在 侧,
y随着x的增大而增大;在 侧,
y随着x的增大而减小,当x= 时,
函数y的值最小,最小值是 ,抛物
线y=2x2在x轴的 方(除顶点外)。
(2)抛物线 在x轴的 方(除顶点外),在对称轴的
左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
(0,0)
y轴
对称轴的右
对称轴的左
0
0
上
下
增大而增大
增大而减小
0
2
二次函数y=ax2的性质
1.顶点坐标及最高点、最低点与对称轴
2.位置及延伸的方向与开口方向
3.最值与增减性
在y轴左右两侧同时向上无限延伸
在y轴左右两侧同时向下无限延伸
开口大小
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2 (a>0)
y= ax2 (a<0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
|a|越小,开口越大.
|a|越大,开口越小.
(0,0)
最低点
最高点
4.开口大小
1、函数y=2x2的图象的开口 ,对称轴 ,顶点是 ;
2、函数y=-3x2的图象的开口 ,对称轴 ,顶点是 ;
向上
向下
y轴
y轴
(0,0)
(0,0)
做一做
(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,
在对称轴 侧,y随着x的增大而增大;在对称轴 侧,
y随着x的增大而减小,当x= 时,函数y的值最小,最小
值是 ,抛物线y=2x2在x轴的 方(除顶点外).
(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
例3.已知 y =(m+1)x 是二次函数且其图象开口向上,求m的值和函数解析式
m2+m
解: 依题意有:
m+1>0 ①
m2+m=2 ②
解②得:m1=-2, m2=1
由①得:m>-1
∴ m=1
此时,二次函数为: y=2x2,
知道就做别客气
当堂检测
3.若二次函数 是开口向上的抛物线,则k的值是( )
A. -3 B. 2 C. 3 D.-3或2
B
4.已知 是二次函数y=x2图象上的一点,则图象上与之对称的点的坐标是( )
A. B. C. D.
5.已知a﹤-1,A(a-1,y1),B(a,y2)C(a+1,y3)
为二次函数y=x2的图象上的三点,则y1,y2,y3的大小关系是( )
B.
D.
B
B
