鲁教版(五四制)六年级数学上册2.8有理数的除法 课件(21张)
文档属性
| 名称 | 鲁教版(五四制)六年级数学上册2.8有理数的除法 课件(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 23:52:00 | ||
图片预览








文档简介
2.8有理数的除法
义务教育教科书六年级上册第二章
教学目标:
1.知识与技能:
(1)理解有理数除法的法则,体会除法与乘法的关系, 能熟练进行有理数的除法运算;
(2)会求一个有理数的倒数。
2.过程与方法:
经历利用已有知识解决新问题的探索过程。
3.情感态度与价值观:
通过探索发现有理数除法法则的过程,发展学生观察、归纳、猜想、验证、表达能力。
笑不笑由你
电视里正在播放精彩的乒乓球比赛,奶奶边看比赛边说:打得好!打得好!可惜播音员不识数……
孙子听了不解地问:人家咋不识数?
奶奶说:明明是两个人在打球,他却说单打;明明是四个人在打球,他却说双打,你说他识数不识数?
你知道为什么奶奶闹了笑话吗?
温故知新
1.有理数的乘法法则是怎样规定的?
两个有理数相乘,同号得正,异号得负,
并把绝对值相乘。0和任何数相乘都得0.
.
2.几个不为0的数相乘,积的符号法则怎样规定的?
由负因数的个数决定,偶数个时为正,奇数个时为负。
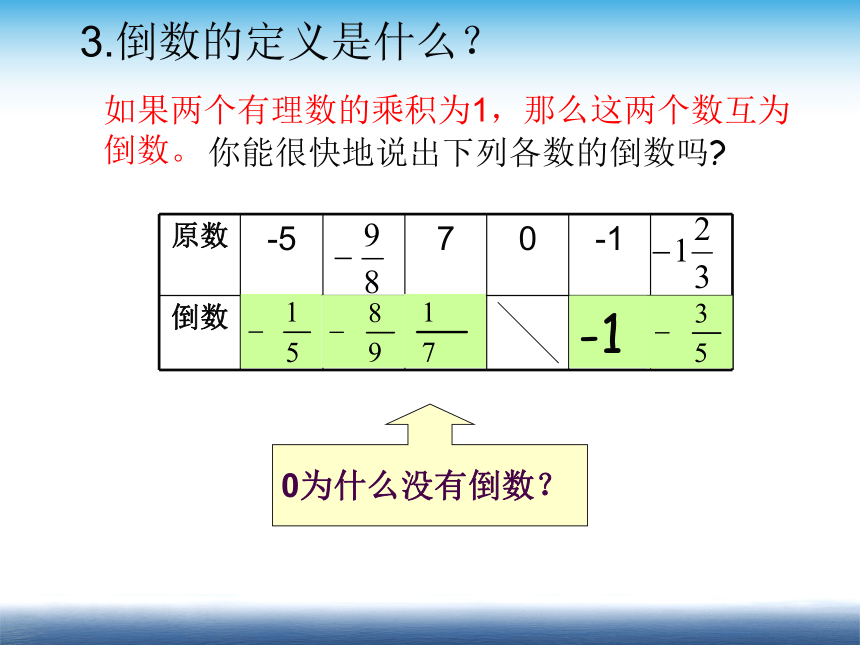
你能很快地说出下列各数的倒数吗?
原数
-5
7
0
-1
倒数
-1
0为什么没有倒数?
3.倒数的定义是什么?
如果两个有理数的乘积为1,那么这两个数互为倒数。
探究学习(一)
快速抢答
(-3)×( ) =-12
( )×(-4)=12
2×( )=-12
( )×5=35
( )×(-2019)=0
除法是乘法的逆运算
你有什么发现?
4
3
-6
7
0
(-12)÷(-3) =
12÷(-4)=
-12÷2=
35÷5=
0÷(-2019)=( )
4
-3
-6
7
0
自主探究,合作交流
有理数的除法法则(一)
对于两个有理数相除,你能得出什么结论?
两个有理数相除,同号得 正 ,异号得 负 ,并把绝对值 相除 .
0除以任何非0的数都得 0 .
注意:0不能作除数
为什么?
学以致用
例1 计算:
(1)
(2)
(3)
(4)
解:
(1)
(2)
(3)
(4)
例题1
训练巩固,反馈矫正(一)
1.计算:
(1)(-18)÷6; (2)(-63)÷(-7); (3)(-36)÷6; (4)1÷(-9); (5)0÷(-8); (6)16÷(-3).
两个有理数相除的运算步骤:
1.确定符号:同号得正,异号得负;
2.确定绝对值;
3.得出结果。
归纳总结
计算并比较下列各组数的计算结果:
(1)
(2)
自主探究,合作交流
有什么特点?
你能得出什么结论?
(-12)÷(-4)=
(-12)×(- )=
(-18)÷(+3)=
(-18)×(+ )=
数学语言:除以一个数等于 乘以这个数的 倒数。
有理数的除法法则(二)
符号表示:a÷b=a×
例2 计算:
(2)
(3)
(4)
学以致用
运算步骤:定号;除法变乘法;除数变倒数
(1)
训练巩固,反馈矫正(二)
1.计算:
(1)8×(-14)÷(- 0.6 );
(2)-3.5÷(8.5-0.5)÷(- 7 )
(3)-12÷(-2.5+6).
法则一:两个有理数相除,同号得正,异号得负,并把绝对值 相除 .0除以任何非0的数都得 0 .
法则二:除以一个数等于乘以这个数的倒数.
展示收获,归纳总结
分层检测,和谐发展
1.下列说法正确的是( )
A.倒数是本身的数只有1 B.有理数b的倒数是1/b
C.任何数除以0仍得0 D.0乘以任何数,其积为0
2.计算-3.5÷0.5×(-2)的值为( )
A.-13 B.13 C.-14 D.14
3.若在数轴上表示两个有理数的点分别在原点的两侧,则这两个数的商是( )
A.正数 B.负数 C.零
D.可能是正数也可能是负数
4.计算-13÷(-3)×(-3)的值为( )
A.-13 B.13 C.-27 D.27
拓展延伸,综合应用
1.已知|x|=4,|y|=2,且xy<0,则y÷x的值等于______.
2.已知有理数a,b,c在数轴上所对应的点如图所示,则a÷(b+c)__0.
一、必做题
1、如果两个有理数的商等于0,则( )
A.两个数中有一个数为0 B.两数都为0
C.被除数为0,除数不为0 D.被除数不为0,除数为0
2.计算:
(1) (-0.12)÷(-0.6)
(2) 0÷(-2019)
(3) (-2) ÷
(4) -2.1÷(-0.2)÷
二、选做题
1.计算
(2)
(3)
(1)
再见 !
义务教育教科书六年级上册第二章
教学目标:
1.知识与技能:
(1)理解有理数除法的法则,体会除法与乘法的关系, 能熟练进行有理数的除法运算;
(2)会求一个有理数的倒数。
2.过程与方法:
经历利用已有知识解决新问题的探索过程。
3.情感态度与价值观:
通过探索发现有理数除法法则的过程,发展学生观察、归纳、猜想、验证、表达能力。
笑不笑由你
电视里正在播放精彩的乒乓球比赛,奶奶边看比赛边说:打得好!打得好!可惜播音员不识数……
孙子听了不解地问:人家咋不识数?
奶奶说:明明是两个人在打球,他却说单打;明明是四个人在打球,他却说双打,你说他识数不识数?
你知道为什么奶奶闹了笑话吗?
温故知新
1.有理数的乘法法则是怎样规定的?
两个有理数相乘,同号得正,异号得负,
并把绝对值相乘。0和任何数相乘都得0.
.
2.几个不为0的数相乘,积的符号法则怎样规定的?
由负因数的个数决定,偶数个时为正,奇数个时为负。
你能很快地说出下列各数的倒数吗?
原数
-5
7
0
-1
倒数
-1
0为什么没有倒数?
3.倒数的定义是什么?
如果两个有理数的乘积为1,那么这两个数互为倒数。
探究学习(一)
快速抢答
(-3)×( ) =-12
( )×(-4)=12
2×( )=-12
( )×5=35
( )×(-2019)=0
除法是乘法的逆运算
你有什么发现?
4
3
-6
7
0
(-12)÷(-3) =
12÷(-4)=
-12÷2=
35÷5=
0÷(-2019)=( )
4
-3
-6
7
0
自主探究,合作交流
有理数的除法法则(一)
对于两个有理数相除,你能得出什么结论?
两个有理数相除,同号得 正 ,异号得 负 ,并把绝对值 相除 .
0除以任何非0的数都得 0 .
注意:0不能作除数
为什么?
学以致用
例1 计算:
(1)
(2)
(3)
(4)
解:
(1)
(2)
(3)
(4)
例题1
训练巩固,反馈矫正(一)
1.计算:
(1)(-18)÷6; (2)(-63)÷(-7); (3)(-36)÷6; (4)1÷(-9); (5)0÷(-8); (6)16÷(-3).
两个有理数相除的运算步骤:
1.确定符号:同号得正,异号得负;
2.确定绝对值;
3.得出结果。
归纳总结
计算并比较下列各组数的计算结果:
(1)
(2)
自主探究,合作交流
有什么特点?
你能得出什么结论?
(-12)÷(-4)=
(-12)×(- )=
(-18)÷(+3)=
(-18)×(+ )=
数学语言:除以一个数等于 乘以这个数的 倒数。
有理数的除法法则(二)
符号表示:a÷b=a×
例2 计算:
(2)
(3)
(4)
学以致用
运算步骤:定号;除法变乘法;除数变倒数
(1)
训练巩固,反馈矫正(二)
1.计算:
(1)8×(-14)÷(- 0.6 );
(2)-3.5÷(8.5-0.5)÷(- 7 )
(3)-12÷(-2.5+6).
法则一:两个有理数相除,同号得正,异号得负,并把绝对值 相除 .0除以任何非0的数都得 0 .
法则二:除以一个数等于乘以这个数的倒数.
展示收获,归纳总结
分层检测,和谐发展
1.下列说法正确的是( )
A.倒数是本身的数只有1 B.有理数b的倒数是1/b
C.任何数除以0仍得0 D.0乘以任何数,其积为0
2.计算-3.5÷0.5×(-2)的值为( )
A.-13 B.13 C.-14 D.14
3.若在数轴上表示两个有理数的点分别在原点的两侧,则这两个数的商是( )
A.正数 B.负数 C.零
D.可能是正数也可能是负数
4.计算-13÷(-3)×(-3)的值为( )
A.-13 B.13 C.-27 D.27
拓展延伸,综合应用
1.已知|x|=4,|y|=2,且xy<0,则y÷x的值等于______.
2.已知有理数a,b,c在数轴上所对应的点如图所示,则a÷(b+c)__0.
一、必做题
1、如果两个有理数的商等于0,则( )
A.两个数中有一个数为0 B.两数都为0
C.被除数为0,除数不为0 D.被除数不为0,除数为0
2.计算:
(1) (-0.12)÷(-0.6)
(2) 0÷(-2019)
(3) (-2) ÷
(4) -2.1÷(-0.2)÷
二、选做题
1.计算
(2)
(3)
(1)
再见 !
