新人教版七年级数学4.2直线、射线、线段(第二课时)课件(38张PPT)
文档属性
| 名称 | 新人教版七年级数学4.2直线、射线、线段(第二课时)课件(38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 22:26:27 | ||
图片预览






文档简介
义务教育教科书 数学 七年级 上册
4.2 直线、射线、线段
(第1课时 表示法)
一、直线的基本性质:
A
B
经过两点有一条直线,并且只有一条直线。
或简述为:
两点确定一条直线。
A
B
A
B
A
B
探究 联系与区别
你发现直线、射线、线段有哪些联系与区别?
类型
线段
射线
直线
端点数
2个
延伸
度量
可度量
1个
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可度量
联系:
线段向一端无限延长形成射线,向两端无限延长形成直线
二、直线、射线、线段的区别与联系:
射线、线段都是直线的一部分。
无
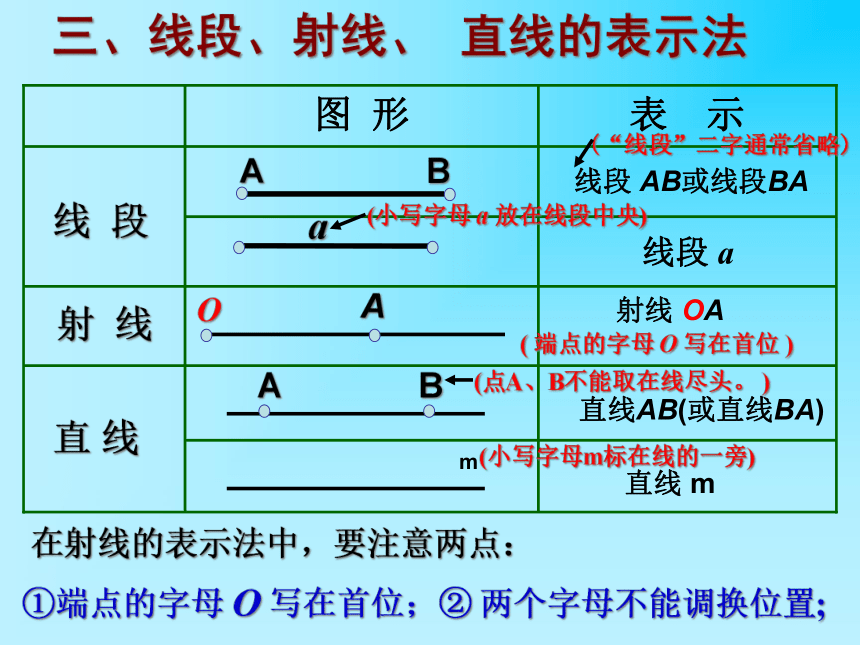
三、线段、射线、 直线的表示法
图 形
表 示
射 线
O
A
A
B
a
直 线
线 段
(小写字母 a 放在线段中央)
( 端点的字母 O 写在首位 )
在射线的表示法中,要注意两点:
①端点的字母 O 写在首位;② 两个字母不能调换位置;
(点A、B不能取在线尽头。 )
m
(小写字母m标在线的一旁)
A
B
线段 AB或线段BA
线段 a
射线 OA
直线AB(或直线BA)
直线 m
(“线段”二字通常省略)
如何用数学符号表示下列的直线、线段、射线?
注意问题:(1)线段、直线表示与字母顺序无关
(2)射线表示有方向性,端点在前,射线上任意一点在后
学一学,
议一议
A
B
表示:直线 AB(或直线BA)
表示:直线
A
B
表示:线段 AB(或线段BA)
表示:射线 OA
表示:线段 a
a
表示:射线 或射线AB
O
A
A
B
判断:
1、射线是直线的一部分。 ( )
2、线段是射线的一部分。 ( )
3、画一条射线,使它的长度为3cm。 ( )
4、线段AB和线段BA是同一条线段。 ( )
5、射线OP和射线PO是同一条射线。 ( )
6、如图,画一条线段ab。 ( )
a
b
针对训练
√
√
√
×
×
×
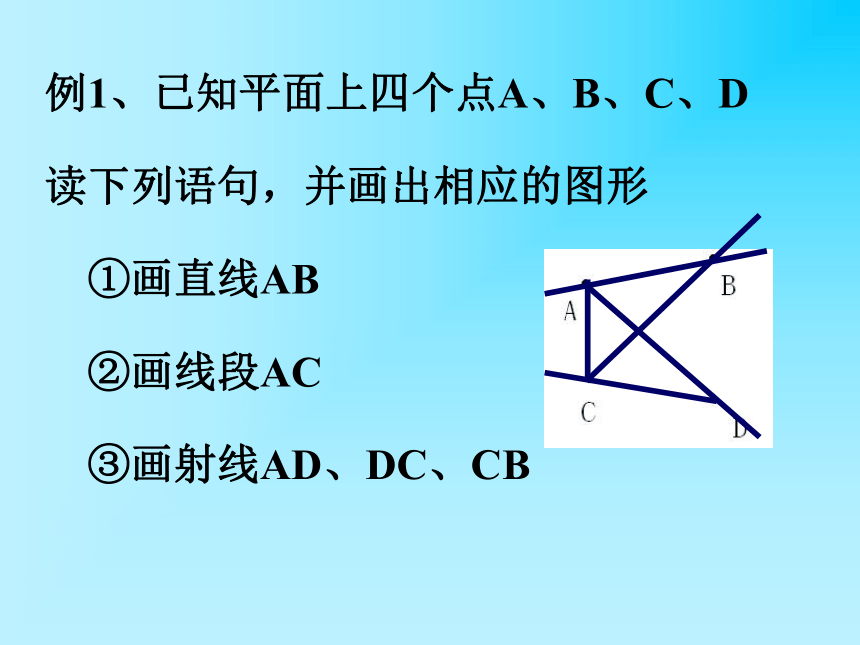
例1、已知平面上四个点A、B、C、D
读下列语句,并画出相应的图形
①画直线AB
②画线段AC
③画射线AD、DC、CB
(1)直线EF经过点C
1. 按下列语句画出图形.
E
F
C
随堂练习一
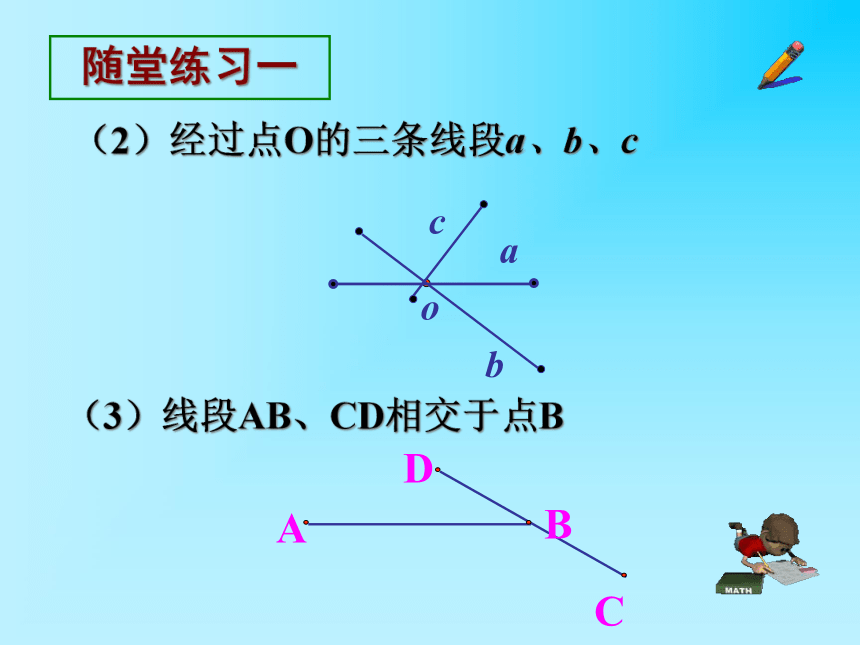
(2)经过点O的三条线段a、b、c
(3)线段AB、CD相交于点B
(2)经过点O的三条线段a、b、c
o
b
c
a
随堂练习一
(3)线段AB、CD相交于点B
B
D
A
C
l
A
点A在直线 l 上
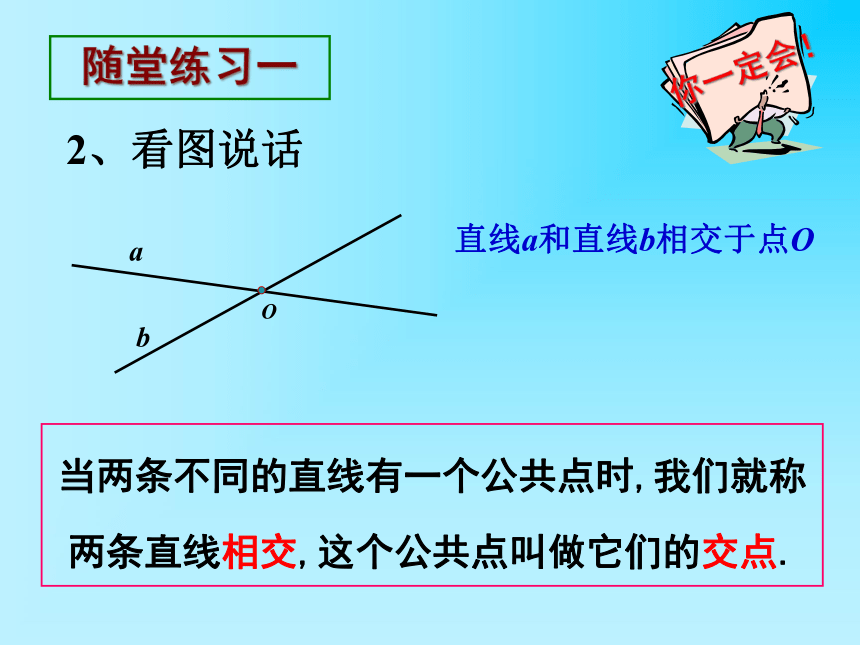
2、看图说话
点A在直线 l 外
l
A
点与直线的位置关系:
1.一个点在一条直线上,也可以说这条直线经过这个点.
2.一个点在一条直线外,也可以说这条直线不经过这个点.
随堂练习一
O
a
b
直线a和直线b相交于点O
当两条不同的直线有一个公共点时,我们就称两条直线相交,这个公共点叫做它们的交点.
2、看图说话
随堂练习一
你一定会!
A
B
E
C
D
解:有10条线段分别是:
线段AB、AC、AD、AE、BC、 BD、BE、CD、CE、DE.
例2.指出下图中线段、射线、直线分别有多少条?
有8条射线
只有1条直线,是直线BC
莞城
厚街
虎门
长安
深圳
答:10种
1、往返莞城、深圳两地的汽车,中途需要停靠厚街、虎门、长安三个站点,根据你所学的知识回答: 需要制定多少种不同的票价?
A B C D E
数学问题
实际问题
转 化 为
随堂练习二
教室里共有3位同学,如果每位
同学都要和其他的人握一次手,
那么他们一共握手 次;
若是 4 位同学,一共握手 次;
若是 5 位同学,一共握手 次;
若是 n 位同学,一共握手 次.
实践与
4.2 直线、射线、线段(2)
----线段的大小比较
义务教育教科书 数学 七年级 上册
直线公理
经过两点有一条直线,并且只有一条直线。
(两点确定一条直线。)
直线、线段、射线的表示
用两个大写字母表示;
用一个小写字母表示。
知识回顾
直线的表示
A
B
l
直线AB
直线l
线段的表示
A
B
a
线段AB
线段a
射线的表示
O
A
射线OA
l
射线l
知识回顾
如何比较两个人的身高?
我身高1.53米,
比你高3厘米。
我身高1.5米。
问题情境
看下面这三幅图片谁高谁矮?你是依据什么判断的 ?
怎样比较两条线段的大小(长短)?
A
B
C
D
两条线段的大小(长短)关系:
(1)AB > CD;
(2)AB = CD;
(3)AB < CD;
探索新知
观察下列三组图形,你能看出每组图形中线段a与b的长短吗?
a
b
a
b
a
b
(1)
(3)
(2)
第一种方法:
用一把尺子量出两根绳子的长度,再进行比较.
3.1cm
4.1cm
1
2
3
5
4
6
7
8
1
2
3
5
4
6
7
8
0
度 量 法
第二种:
先把两根绳子的一端重合,另一端落在同侧,根据另一端落下的位置来比较.
①
②
③
C
D
AB=CD
AB>EF
ABE
F
M
N
E
F
M
N
C
D
A
B
试比较绳子AB与绳子CD、绳子EF、绳子MN的大小?
叠 合 法
叠合法——从“形”的角度比较.
度量法——从“数值”的角度比较.
比较线段长短的两种方法
比较两条线段大小(长短)的方法:
目测法;
直接观察,目测判断。
(不准确,也不十分可靠,不建议采用)
度量法;
用刻度尺分别量出线段AB、线段CD的长度,再比较线段AB、线段CD的长短(大小)。
(近似值)
叠合法。
将一条线段放在另一条线段上,使它们的一个端点重合,观察另一个端点的位置关系。
探索新知
用叠合法比较两条线段大小(长短):
C
D
A
B
(1)
A
B
(2)
(3)
A
B
A
B
C
D
C
D
C
D
AB > CD
AB < CD
AB = CD
两条线段比较长短会有几种情况?
探索新知
1.(1)用刻度尺量出下图中三角形三条边的长:
AC= cm;BC= cm;AB= cm;
(2)用“=”、“<”或“>”填入下面的空格:
AC BC,AC AB,AB BC.
2.用圆规比较下列各对线段的长短:
(1) (2)
a
b
d
A
B
C
c
教材P131 “练习”第1题
AB > AC
AB = AC
AB < AC
随堂练习
怎样画一条线段等于已知线段?
画一条线段AB=线段a。
a
方法一:
先用刻度尺量出线段a的长度,再画一条等于这个长度的线段AB。
方法二:
尺规作图:
作法:
(1)作射线AC;
(2)在射线AC上截取AB = a。
则线段AB就是所求作的线段。
A
C
B
探索新知
已知:线段m、n。(如图)
求作:线段AC,使AC = m + n。
m
n
作法:
(1)作射线AM;
A
M
B
C
则线段AC就是所求作的线段。
(2)在射线AM上顺次截取AB = m,BC = n。
探索新知
已知:线段m、n。(如图)
求作:线段AC,使AC = m - n。
m
n
作法:
(1)作射线AM;
A
M
(2)在射线AM上截取AB = m。
B
(3)在线段AB上截取BC = n。
C
则线段AC就是所求作的线段。
随堂练习
怎样的点是线段的中点?
操作:
把纸条对折,找出它的中点。
定义:
把线段分成相等的两条线段的点,叫做这条线段的中点。
A M B
因为点M是线段AB的中点,
所以 AM=BM= AB
说明:
线段的中点必须在线段上。
把线段分成相等的三条线段的点,叫做这条线段的三等分点。
探索新知
已知线段AB = 4cm,延长AB到C,使BC = 2AB,若D为AB的中点,则线段DC 的长为 cm。
10
A
B
C
D
4cm
8cm
2cm
2cm + 8cm = 10cm
随堂练习
A、B、C、D四点在同一直线上(如图),若AB = CD,
则AC CD。(填“>”、“=”或“<”)
已知A、B是数轴上的两点,AB = 2,点B表示的数是-1,
那么点A表示的数是 。
A B C D
=
1或-3
-5 -4 -3 -2 -1 0 1 2
B
A
A
随堂练习
比较两条线段大小(长短)的方法:
目测法;
度量法;
叠合法。
基本作图:作一条线段等于已知线段。
线段的中点。
A M B
因为点M是线段AB的中点,
所以 AM=BM= AB
课堂小结
1、已知:线段a、b、c(如图)。
求作:线段AB,使AB = a + b – c。
2、如图,线段AB = 6cm,C是它的一个三等分点,D是它的中点,则CD = cm。
3、已知:点A、B、C在同一直线上,AB = 8cm,BC = 6cm,点M、N分别是AB、BC的中点。求:线段MN的长。
A D C B
a
b
c
课 后 作 业
数学是七彩的阳光!
平时要做有心人,
注意观察和比较,
勤加思考与探索,
定会发现许多奥妙。
相信自己,就是第一!
4.2 直线、射线、线段
(第1课时 表示法)
一、直线的基本性质:
A
B
经过两点有一条直线,并且只有一条直线。
或简述为:
两点确定一条直线。
A
B
A
B
A
B
探究 联系与区别
你发现直线、射线、线段有哪些联系与区别?
类型
线段
射线
直线
端点数
2个
延伸
度量
可度量
1个
向一个方向无限延伸
不可度量
无端点
向两个方向无限延伸
不可度量
联系:
线段向一端无限延长形成射线,向两端无限延长形成直线
二、直线、射线、线段的区别与联系:
射线、线段都是直线的一部分。
无
三、线段、射线、 直线的表示法
图 形
表 示
射 线
O
A
A
B
a
直 线
线 段
(小写字母 a 放在线段中央)
( 端点的字母 O 写在首位 )
在射线的表示法中,要注意两点:
①端点的字母 O 写在首位;② 两个字母不能调换位置;
(点A、B不能取在线尽头。 )
m
(小写字母m标在线的一旁)
A
B
线段 AB或线段BA
线段 a
射线 OA
直线AB(或直线BA)
直线 m
(“线段”二字通常省略)
如何用数学符号表示下列的直线、线段、射线?
注意问题:(1)线段、直线表示与字母顺序无关
(2)射线表示有方向性,端点在前,射线上任意一点在后
学一学,
议一议
A
B
表示:直线 AB(或直线BA)
表示:直线
A
B
表示:线段 AB(或线段BA)
表示:射线 OA
表示:线段 a
a
表示:射线 或射线AB
O
A
A
B
判断:
1、射线是直线的一部分。 ( )
2、线段是射线的一部分。 ( )
3、画一条射线,使它的长度为3cm。 ( )
4、线段AB和线段BA是同一条线段。 ( )
5、射线OP和射线PO是同一条射线。 ( )
6、如图,画一条线段ab。 ( )
a
b
针对训练
√
√
√
×
×
×
例1、已知平面上四个点A、B、C、D
读下列语句,并画出相应的图形
①画直线AB
②画线段AC
③画射线AD、DC、CB
(1)直线EF经过点C
1. 按下列语句画出图形.
E
F
C
随堂练习一
(2)经过点O的三条线段a、b、c
(3)线段AB、CD相交于点B
(2)经过点O的三条线段a、b、c
o
b
c
a
随堂练习一
(3)线段AB、CD相交于点B
B
D
A
C
l
A
点A在直线 l 上
2、看图说话
点A在直线 l 外
l
A
点与直线的位置关系:
1.一个点在一条直线上,也可以说这条直线经过这个点.
2.一个点在一条直线外,也可以说这条直线不经过这个点.
随堂练习一
O
a
b
直线a和直线b相交于点O
当两条不同的直线有一个公共点时,我们就称两条直线相交,这个公共点叫做它们的交点.
2、看图说话
随堂练习一
你一定会!
A
B
E
C
D
解:有10条线段分别是:
线段AB、AC、AD、AE、BC、 BD、BE、CD、CE、DE.
例2.指出下图中线段、射线、直线分别有多少条?
有8条射线
只有1条直线,是直线BC
莞城
厚街
虎门
长安
深圳
答:10种
1、往返莞城、深圳两地的汽车,中途需要停靠厚街、虎门、长安三个站点,根据你所学的知识回答: 需要制定多少种不同的票价?
A B C D E
数学问题
实际问题
转 化 为
随堂练习二
教室里共有3位同学,如果每位
同学都要和其他的人握一次手,
那么他们一共握手 次;
若是 4 位同学,一共握手 次;
若是 5 位同学,一共握手 次;
若是 n 位同学,一共握手 次.
实践与
4.2 直线、射线、线段(2)
----线段的大小比较
义务教育教科书 数学 七年级 上册
直线公理
经过两点有一条直线,并且只有一条直线。
(两点确定一条直线。)
直线、线段、射线的表示
用两个大写字母表示;
用一个小写字母表示。
知识回顾
直线的表示
A
B
l
直线AB
直线l
线段的表示
A
B
a
线段AB
线段a
射线的表示
O
A
射线OA
l
射线l
知识回顾
如何比较两个人的身高?
我身高1.53米,
比你高3厘米。
我身高1.5米。
问题情境
看下面这三幅图片谁高谁矮?你是依据什么判断的 ?
怎样比较两条线段的大小(长短)?
A
B
C
D
两条线段的大小(长短)关系:
(1)AB > CD;
(2)AB = CD;
(3)AB < CD;
探索新知
观察下列三组图形,你能看出每组图形中线段a与b的长短吗?
a
b
a
b
a
b
(1)
(3)
(2)
第一种方法:
用一把尺子量出两根绳子的长度,再进行比较.
3.1cm
4.1cm
1
2
3
5
4
6
7
8
1
2
3
5
4
6
7
8
0
度 量 法
第二种:
先把两根绳子的一端重合,另一端落在同侧,根据另一端落下的位置来比较.
①
②
③
C
D
AB=CD
AB>EF
AB
F
M
N
E
F
M
N
C
D
A
B
试比较绳子AB与绳子CD、绳子EF、绳子MN的大小?
叠 合 法
叠合法——从“形”的角度比较.
度量法——从“数值”的角度比较.
比较线段长短的两种方法
比较两条线段大小(长短)的方法:
目测法;
直接观察,目测判断。
(不准确,也不十分可靠,不建议采用)
度量法;
用刻度尺分别量出线段AB、线段CD的长度,再比较线段AB、线段CD的长短(大小)。
(近似值)
叠合法。
将一条线段放在另一条线段上,使它们的一个端点重合,观察另一个端点的位置关系。
探索新知
用叠合法比较两条线段大小(长短):
C
D
A
B
(1)
A
B
(2)
(3)
A
B
A
B
C
D
C
D
C
D
AB > CD
AB < CD
AB = CD
两条线段比较长短会有几种情况?
探索新知
1.(1)用刻度尺量出下图中三角形三条边的长:
AC= cm;BC= cm;AB= cm;
(2)用“=”、“<”或“>”填入下面的空格:
AC BC,AC AB,AB BC.
2.用圆规比较下列各对线段的长短:
(1) (2)
a
b
d
A
B
C
c
教材P131 “练习”第1题
AB > AC
AB = AC
AB < AC
随堂练习
怎样画一条线段等于已知线段?
画一条线段AB=线段a。
a
方法一:
先用刻度尺量出线段a的长度,再画一条等于这个长度的线段AB。
方法二:
尺规作图:
作法:
(1)作射线AC;
(2)在射线AC上截取AB = a。
则线段AB就是所求作的线段。
A
C
B
探索新知
已知:线段m、n。(如图)
求作:线段AC,使AC = m + n。
m
n
作法:
(1)作射线AM;
A
M
B
C
则线段AC就是所求作的线段。
(2)在射线AM上顺次截取AB = m,BC = n。
探索新知
已知:线段m、n。(如图)
求作:线段AC,使AC = m - n。
m
n
作法:
(1)作射线AM;
A
M
(2)在射线AM上截取AB = m。
B
(3)在线段AB上截取BC = n。
C
则线段AC就是所求作的线段。
随堂练习
怎样的点是线段的中点?
操作:
把纸条对折,找出它的中点。
定义:
把线段分成相等的两条线段的点,叫做这条线段的中点。
A M B
因为点M是线段AB的中点,
所以 AM=BM= AB
说明:
线段的中点必须在线段上。
把线段分成相等的三条线段的点,叫做这条线段的三等分点。
探索新知
已知线段AB = 4cm,延长AB到C,使BC = 2AB,若D为AB的中点,则线段DC 的长为 cm。
10
A
B
C
D
4cm
8cm
2cm
2cm + 8cm = 10cm
随堂练习
A、B、C、D四点在同一直线上(如图),若AB = CD,
则AC CD。(填“>”、“=”或“<”)
已知A、B是数轴上的两点,AB = 2,点B表示的数是-1,
那么点A表示的数是 。
A B C D
=
1或-3
-5 -4 -3 -2 -1 0 1 2
B
A
A
随堂练习
比较两条线段大小(长短)的方法:
目测法;
度量法;
叠合法。
基本作图:作一条线段等于已知线段。
线段的中点。
A M B
因为点M是线段AB的中点,
所以 AM=BM= AB
课堂小结
1、已知:线段a、b、c(如图)。
求作:线段AB,使AB = a + b – c。
2、如图,线段AB = 6cm,C是它的一个三等分点,D是它的中点,则CD = cm。
3、已知:点A、B、C在同一直线上,AB = 8cm,BC = 6cm,点M、N分别是AB、BC的中点。求:线段MN的长。
A D C B
a
b
c
课 后 作 业
数学是七彩的阳光!
平时要做有心人,
注意观察和比较,
勤加思考与探索,
定会发现许多奥妙。
相信自己,就是第一!
