2020-2021学年北师大版八年级上册数学7.3《平行线的判定》同步练习(Word版 有答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级上册数学7.3《平行线的判定》同步练习(Word版 有答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 139.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览


文档简介
第三节
平行线的判定
一、选择题
1.
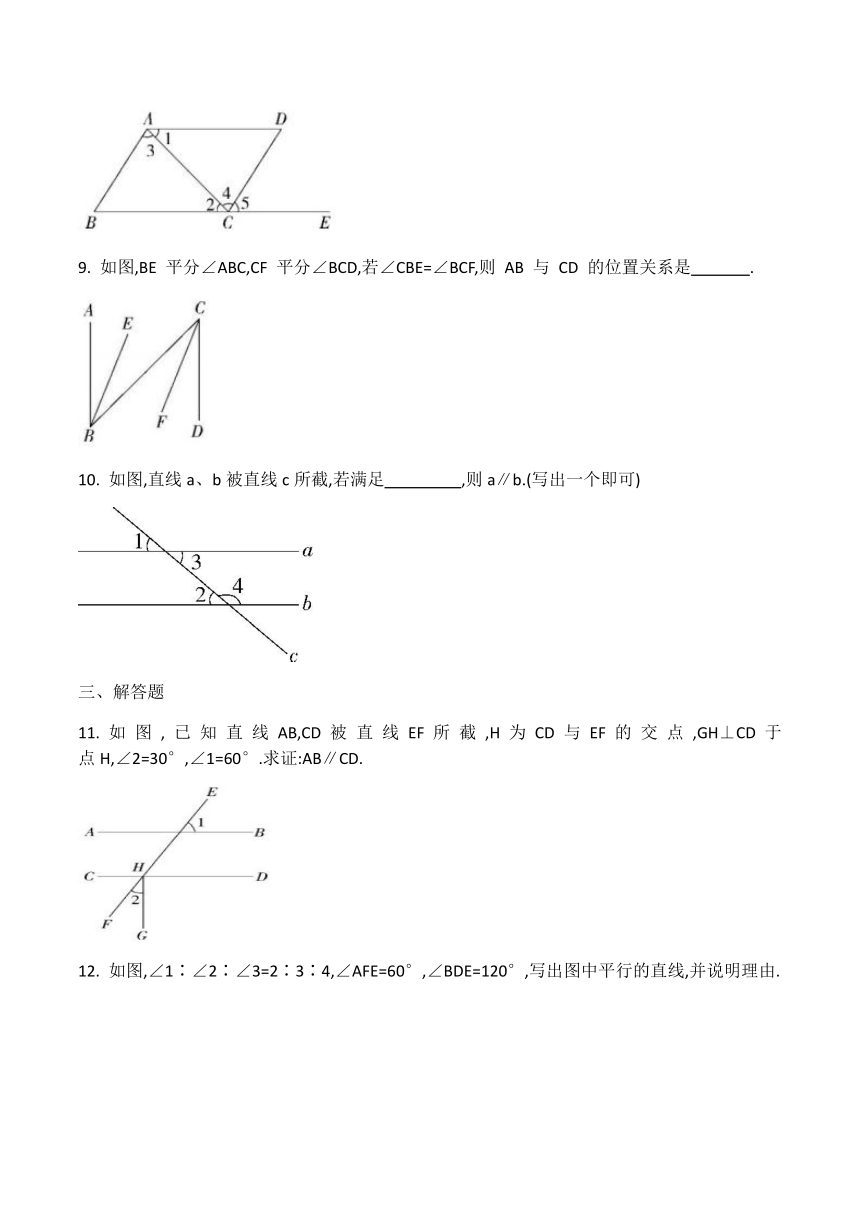
如图,将木条
a,b
与
c
钉在一起,∠1=70°,∠2=50°.要使木条
a
与
b
平行,木条
a
旋转的度数至少是(
)
A.10°
B.20°
C.50°
D.70°
2.
如图,下列能判定
AB∥EF
的条件有(
)
①∠B+∠BFE=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5.
A.1
个
B.2
个
C.3
个
D.4
个
3.
如图所示,点
E
在
BC
的延长线上,下列条件中不能判定
AB∥CD
的是(
)
A.∠3=∠4
B.∠1=∠2
C.∠B=∠DCE
D.∠D+∠DAB=180°
4.
将一块直角三角板ABC按如图所示的方式放置,若∠ABC=30°,A、B两点分别落在直线m,n上,∠1=20°,下列条件中能判定直线m∥n的是( )
A.∠2=20° ????B.∠2=30°
C.∠2=45° ????D.∠2=50°
5.
如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠2=∠4 ????B.∠1+∠4=180°
C.∠5=∠4 ????D.∠1=∠3
二、填空题
6.
如图所示,已知∠C=100°,若增加一个条件,使得
AB∥CD,试写出符合要求的一个条件:
.
7.
如图所示的是利用直尺和三角板过已知直线
l
外一点
P
作直线
l
的平行线的方法,其理由是
.
8.
如图,下列条件中:
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
能判定
AB∥CD
的条件为
(填写所有正确的序号).
9.
如图,BE
平分∠ABC,CF
平分∠BCD,若∠CBE=∠BCF,则
AB
与
CD
的位置关系是
.
10.
如图,直线a、b被直线c所截,若满足????
,则a∥b.(写出一个即可)
三、解答题
11.
如
图
,
已
知
直
线
AB,CD
被
直
线
EF
所
截
,H
为
CD
与
EF
的
交
点
,GH⊥CD
于
点H,∠2=30°,∠1=60°.求证:AB∥CD.
12.
如图,∠1∶∠2∶∠3=2∶3∶4,∠AFE=60°,∠BDE=120°,写出图中平行的直线,并说明理由.
13.
如图,已知∠1=∠2,∠3+∠4=180°,求证:AB∥EF.
14.
如图,已知∠1=∠2,再添加什么条件可使AB∥CD成立?根据你添加的条件证明AB∥CD.
15.
我们知道,光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.光线从空气中射入水中,再从水中射入空气中的示意图如图所示,由于折射率相同,因此∠1=∠4,∠2=∠3.请你用所学知识判断直线c与d是否平行,并说明理由.
答案
1.B
2.C
3.A
4.D
5.D
6.
答案不唯一,如∠BEC=80°或∠AEC=100°或∠FEB=100°
7.
同位角相等,两直线平行
8.
①③④
9.
平行
10.
∠1=∠2(或∠2=∠3或∠3+∠4=180°)
11.证明∵GH⊥CD(已知),
∴∠CHG=90°(垂直的定义).
又∵∠2=30°(已知),∴∠CHF=60°,
∴∠DHE=60°(对顶角相等).
又∵∠1=60°(已知),∴∠1=∠DHE,
∴AB∥CD(同位角相等,两直线平行).
12.
EF∥BC,DE∥AB.
理由:∵∠1∶∠2∶∠3=2∶3∶4,∠1+∠2+∠3=180°,
∴∠1=40°,∠2=60°,∠3=80°,
又∵∠AFE=60°,∠BDE=120°,
∴∠AFE=∠2,∠BDE+∠2=180°,
∴DE∥AB,EF∥BC.
13.证明
∵∠1=∠2,
∴AB∥CD,
∵∠3+∠4=180°,
∴CD∥EF,∴AB∥EF.
14.
(1)添加条件:∠EBN=∠FDN.
理由:∵∠1=∠2,∠EBN=∠FDN,
∴∠1+∠EBN=∠2+∠FDN,即∠ABN=∠CDN,
∴AB∥CD(同位角相等,两直线平行).
(2)添加条件:∠EBM=∠FDM.
理由:∵∠1=∠2,∠EBM=∠FDM,
∴∠EBM-∠1=∠FDM-∠2,即∠ABM=∠CDM,
∴AB∥CD(同位角相等,两直线平行).
(3)添加条件:∠EBD+∠BDF=180°.
理由:∵∠EBD+∠BDF=180°,
∴∠EBD+∠BDC+∠2=180°.
∵∠1=∠2,
∴∠EBD+∠BDC+∠1=180°,即∠ABD+∠BDC=180°.
∴AB∥CD(同旁内角互补,两直线平行).
15.
??c∥d.理由如下:如图所示.
∵∠2+∠5=∠3+∠6=180°,∠2=∠3,∴∠5=∠6.
∵∠1=∠4,∴∠1+∠5=∠4+∠6(等式的性质),
∴c∥d(内错角相等,两直线平行).
平行线的判定
一、选择题
1.
如图,将木条
a,b
与
c
钉在一起,∠1=70°,∠2=50°.要使木条
a
与
b
平行,木条
a
旋转的度数至少是(
)
A.10°
B.20°
C.50°
D.70°
2.
如图,下列能判定
AB∥EF
的条件有(
)
①∠B+∠BFE=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5.
A.1
个
B.2
个
C.3
个
D.4
个
3.
如图所示,点
E
在
BC
的延长线上,下列条件中不能判定
AB∥CD
的是(
)
A.∠3=∠4
B.∠1=∠2
C.∠B=∠DCE
D.∠D+∠DAB=180°
4.
将一块直角三角板ABC按如图所示的方式放置,若∠ABC=30°,A、B两点分别落在直线m,n上,∠1=20°,下列条件中能判定直线m∥n的是( )
A.∠2=20° ????B.∠2=30°
C.∠2=45° ????D.∠2=50°
5.
如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠2=∠4 ????B.∠1+∠4=180°
C.∠5=∠4 ????D.∠1=∠3
二、填空题
6.
如图所示,已知∠C=100°,若增加一个条件,使得
AB∥CD,试写出符合要求的一个条件:
.
7.
如图所示的是利用直尺和三角板过已知直线
l
外一点
P
作直线
l
的平行线的方法,其理由是
.
8.
如图,下列条件中:
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
能判定
AB∥CD
的条件为
(填写所有正确的序号).
9.
如图,BE
平分∠ABC,CF
平分∠BCD,若∠CBE=∠BCF,则
AB
与
CD
的位置关系是
.
10.
如图,直线a、b被直线c所截,若满足????
,则a∥b.(写出一个即可)
三、解答题
11.
如
图
,
已
知
直
线
AB,CD
被
直
线
EF
所
截
,H
为
CD
与
EF
的
交
点
,GH⊥CD
于
点H,∠2=30°,∠1=60°.求证:AB∥CD.
12.
如图,∠1∶∠2∶∠3=2∶3∶4,∠AFE=60°,∠BDE=120°,写出图中平行的直线,并说明理由.
13.
如图,已知∠1=∠2,∠3+∠4=180°,求证:AB∥EF.
14.
如图,已知∠1=∠2,再添加什么条件可使AB∥CD成立?根据你添加的条件证明AB∥CD.
15.
我们知道,光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.光线从空气中射入水中,再从水中射入空气中的示意图如图所示,由于折射率相同,因此∠1=∠4,∠2=∠3.请你用所学知识判断直线c与d是否平行,并说明理由.
答案
1.B
2.C
3.A
4.D
5.D
6.
答案不唯一,如∠BEC=80°或∠AEC=100°或∠FEB=100°
7.
同位角相等,两直线平行
8.
①③④
9.
平行
10.
∠1=∠2(或∠2=∠3或∠3+∠4=180°)
11.证明∵GH⊥CD(已知),
∴∠CHG=90°(垂直的定义).
又∵∠2=30°(已知),∴∠CHF=60°,
∴∠DHE=60°(对顶角相等).
又∵∠1=60°(已知),∴∠1=∠DHE,
∴AB∥CD(同位角相等,两直线平行).
12.
EF∥BC,DE∥AB.
理由:∵∠1∶∠2∶∠3=2∶3∶4,∠1+∠2+∠3=180°,
∴∠1=40°,∠2=60°,∠3=80°,
又∵∠AFE=60°,∠BDE=120°,
∴∠AFE=∠2,∠BDE+∠2=180°,
∴DE∥AB,EF∥BC.
13.证明
∵∠1=∠2,
∴AB∥CD,
∵∠3+∠4=180°,
∴CD∥EF,∴AB∥EF.
14.
(1)添加条件:∠EBN=∠FDN.
理由:∵∠1=∠2,∠EBN=∠FDN,
∴∠1+∠EBN=∠2+∠FDN,即∠ABN=∠CDN,
∴AB∥CD(同位角相等,两直线平行).
(2)添加条件:∠EBM=∠FDM.
理由:∵∠1=∠2,∠EBM=∠FDM,
∴∠EBM-∠1=∠FDM-∠2,即∠ABM=∠CDM,
∴AB∥CD(同位角相等,两直线平行).
(3)添加条件:∠EBD+∠BDF=180°.
理由:∵∠EBD+∠BDF=180°,
∴∠EBD+∠BDC+∠2=180°.
∵∠1=∠2,
∴∠EBD+∠BDC+∠1=180°,即∠ABD+∠BDC=180°.
∴AB∥CD(同旁内角互补,两直线平行).
15.
??c∥d.理由如下:如图所示.
∵∠2+∠5=∠3+∠6=180°,∠2=∠3,∴∠5=∠6.
∵∠1=∠4,∴∠1+∠5=∠4+∠6(等式的性质),
∴c∥d(内错角相等,两直线平行).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
