沪科版数学九年级上册21.5 第2课时 反比例函数的图象和性质教学课件(46张)
文档属性
| 名称 | 沪科版数学九年级上册21.5 第2课时 反比例函数的图象和性质教学课件(46张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 08:24:29 | ||
图片预览








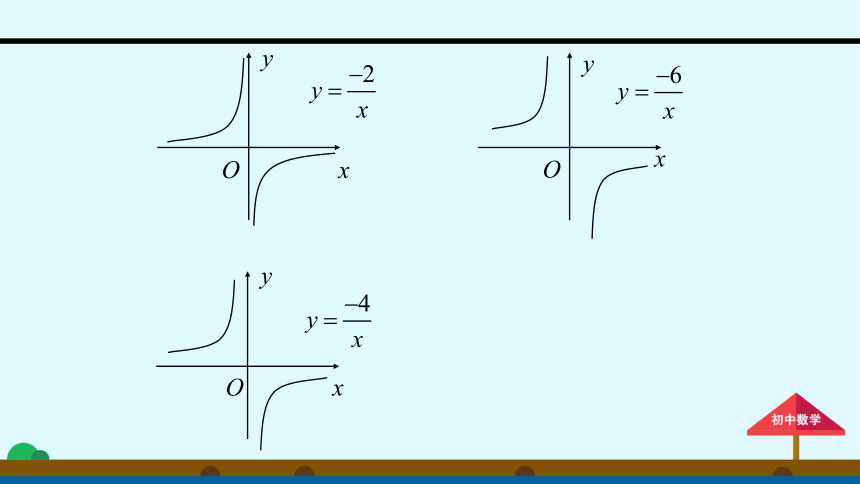
文档简介
(共46张PPT)
第21章
二次函数与反比例函数
沪科版数学九年级上册
21.5
反比例函数
第2课时
反比例函数的图象和性质
学习目标
1.
经历画反比例函数的图象、归纳得到反比例函数的
图象特征和性质的过程
(重点、难点)
2.
会画反比例函数图象,了解和掌握反比例函数的图
象和性质.
(重点)
3.
能够初步应用反比例函数的图象和性质解题.
(重点、
难点)
本节目标
我们已经学习过的函数有哪些?你还记得画这些函数图象时的方法吗?
写出一个反比例函数,你能画出它的图象吗?
引入新知
例1
画反比例函数
与
的图象.
合作探究
提示:画函数的图象步骤一般分为:列表→描点→连线.
需要注意的是在反比例函数中自变量
x
不能为
0.
反比例函数的图象和性质
新知讲解
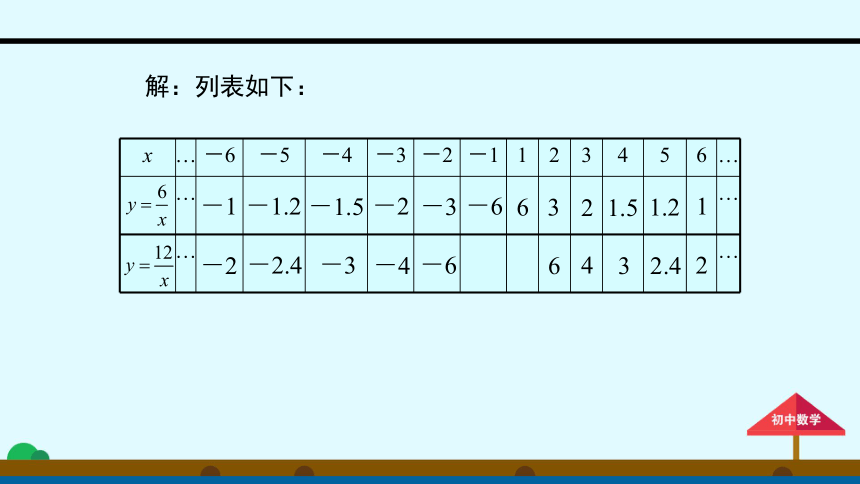
解:列表如下:
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
…
…
…
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
-2
-2.4
-3
-4
-6
6
4
3
2.4
2
O
-2
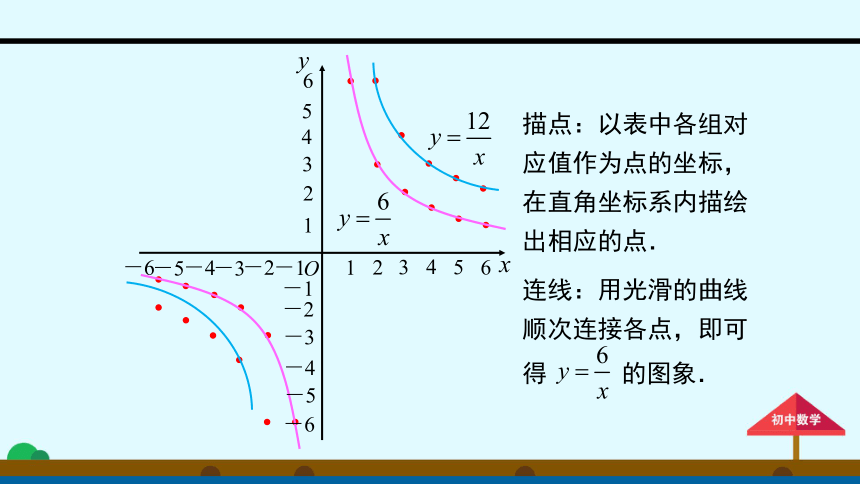
描点:以表中各组对应值作为点的坐标,在直角坐标系内描绘出相应的点.
5
6
x
y
4
3
2
1
1
2
3
4
5
6
-3
-4
-1
-5
-6
-1
-2
-3
-4
-5
-6
连线:用光滑的曲线顺次连接各点,即可
得
的图象.
观察这两个函数图象,回答问题:
思考:
(1)
每个函数图象分别位于哪些象限?
(2)
在每一个象限内,随着x的增大,y如何变化?
你能由它们的解析式说明理由吗?
(3)
对于反比例函数
(k>0),考虑问题(1)(2),
你能得出同样的结论吗?
●由两条曲线组成,且分别位于第一、三象限
它们与
x
轴、y
轴都不相交;
●在每个象限内,y
随
x
的增大而减小.
反比例函数
(k>0)
的图象和性质:
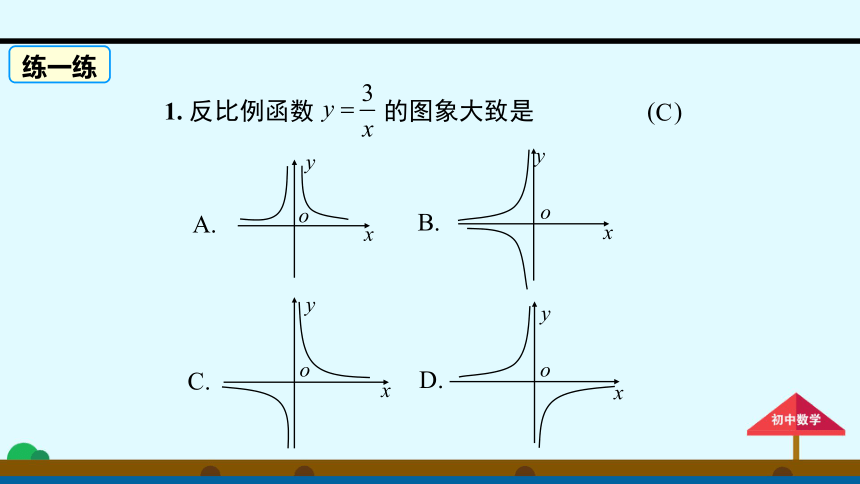
1.
反比例函数
的图象大致是
(
)
C
y
A.
x
y
o
B.
x
o
D.
x
y
o
C.
x
y
o
练一练
2.
已知反比例函数
的图象过点(-2,-3),函
数图象上有两点
A(
,y1),B(5,y2),则
y1与y2
的大小关系为
(
)
A.
y1
>
y2
B.
y1
=
y2
C.
y1
<
y2
D.
无法确定
C
提示:由题可知反比例函数的解析式为
,因为6>0,且
A,B
两点均在该函数图象的第一象限部分,根据
>5,可知y1,y2的大小关系.
观察与思考
当
k
=-2,-4,-6时,反比例函数
的图象,有哪些共同特征?回顾上面我们利用函数图象,从特殊到一般研究反比例函数
(k>0)
的性质的过程,你能用类似的方法研究反比例函数
(k<0)的图象和性质吗?
y
x
O
y
x
O
y
x
O
反比例函数
(k<0)
的图象和性质:
●由两条曲线组成,且分别位于第二、四象限
它们与x轴、y轴都不相交;
●在每个象限内,y随x的增大而增大.
归纳:
(1)
当
k
>
0
时,双曲线的两支分别位于第一、三
象限,在每一象限内,y
随
x
的增大而减小;
(2)
当
k
<
0
时,双曲线的两支分别位于第二、四
象限,在每一象限内,y
随
x
的增大而增大.
一般地,反比例函数
的图象是双曲线,它具有以下性质:
k
的正负决定反比例函数所在的象限和增减性
点(2,y1)和(3,y2)在函数
上,则y1
y2
(填“>”“<”或“=”).
<
练一练
例2
已知反比例函数
,y
随
x
的增大而增大,求a的值.
解:由题意得a2+a-7=-1,且a-1<0.
解得
a=-3.
反比例函数的图象和性质的初步运用
练一练
已知反比例函数
在每个象限内,y
随着
x
的增大而减小,求
m
的值.
解:由题意得
m2-10=-1,且
3m-8>0.
解得
m=3.
例3
已知反比例函数的图象经过点
A
(2,6).
(1)
这个函数的图象位于哪些象限?y
随
x
的增大如
何变化?
解:因为点
A
(2,6)
在第一象限,所以这个函数的
图象位于第一、三象限;
在每一个象限内,y
随
x
的增大而减小.
(2)
点B(3,4),C(
,
),D(2,5)是否在这个
函数的图象上?
解:设这个反比例函数的解析式为
,因为点
A
(2,6)在其图象上,所以有
,解得
k
=12.
因为点
B,C
的坐标都满足该解析式,而点
D的坐标不满足,所以点
B,C
在这个函数的图象上,点
D
不在这个函数的图象上.
所以反比例函数的解析式为
.
(1)
图象的另一支位于哪个象限?常数
m
的取值范围
是什么?
O
x
y
例4
如图,是反比例函数
图象的一支.
根据图象,回答下列问题:
解:因为这个反比例函数图象的一
支位于第一象限,所以另一支
必位于第三象限.
由因为这个函数图象位于第一、
三象限,所以m-5>0,
解得m>5.
(2)
在这个函数图象的某一支上任取点
A
(x1,y1)
和
点B
(x2,y2).
如果x1>x2,那么
y1
和
y2
有怎样的
大小关系?
解:因为
m-5
>
0,所以在这个函数图象的任一支
上,y
都随
x
的增大而减小,因此当x1>x2时,
y1<y2.
(1)
如果这个函数图象经过点(-3,5),求k的值;
(2)如果这个函数图象在它所处的象限内,函数y随x的增大而减小,求k的范围.
例5
已知反比例函数
解:(1)
因为函数图象经过点(-3,5),代入
函数的表达式,得
解方程,得k=-7.
(2)根据题意,有2k-1>0.
解不等式,得
1.
在反比例函数
的图象上分别取点P,Q
向
x
轴、y
轴作垂线,围成面积分别为S1,S2的矩形,
填写下页表格:
合作探究
反比例函数解析式中
k
的几何意义
5
1
2
3
4
-1
5
x
y
O
P
S1
S2
P
(2,2)
Q
(4,1)
S1的值
S2的值
S1与S2的关系
猜想
S1,S2
与
k的关系
4
4
S1=S2
S1=S2=k
-5
-4
-3
-2
1
4
3
2
-3
-2
-4
-5
-1
Q
S1的值
S2的值
S1与S2的关系
猜想与
k
的关系
P
(-1,4)
Q
(-2,2)
2.
若在反比例函数
中也
用同样的方法分别取
P,Q
两点,填写表格:
4
4
S1=S2
S1=S2=-k
y
x
O
P
Q
S1
S2
由前面的探究过程,可以猜想:
若点P是
图象上的任意一点,作
PA
垂直于
x
轴,作
PB
垂直于
y
轴,矩形
AOBP
的面积与k
的关系是S矩形
AOBP=|k|.
y
x
O
P
S
我们就
k
<
0
的情况给出证明:
设点
P
的坐标为
(a,b)
A
B
∵点
P
(a,b)
在函数
的图
象上,
∴
,即
ab=k.
∴
S矩形
AOBP=PB·PA=-a·b=-ab=-k;
若点
P
在第二象限,则
a<0,b>0,
若点
P
在第四象限,则
a>0,b<0,
∴
S矩形
AOBP=PB·PA
=a·
(-b)=-ab=-k.
B
P
A
综上,S矩形
AOBP=|k|.
自己尝试证明
k
>
0的情况.
点
Q
是其图象上的任意一
点,作
QA
垂直于
y
轴,作
QB
垂直于x
轴,矩形AOBQ
的面积与
k
的关系是
S矩形AOBQ=
.
推理:△QAO与△QBO的
面积和
k
的关系是
S△QAO=S△QBO=
.
Q
对于反比例函数
,
A
B
|k|
y
x
O
归纳:
反比例函数的面积不变性
A.
SA
>SB>SC
B.
SAC.
SA
=SB=SC
D.
SA1.
如图,在函数
(x>0)的图像上有三点A,B
,
C,过这三点分别向
x
轴、y
轴作垂线,过每一点
所作的两条垂线与x轴、
y轴围成的矩形的面积分
别为SA
,SB,SC,则
(
)
y
x
O
A
B
C
C
练一练
2.
如图,过反比例函数
图象上的一点
P,作
PA⊥x
轴于A.
若△POA
的面积为
6,则
k
=
.
-12
提示:当反比例函数图象在第二、四象限时,注意
k<0.
y
x
O
P
A
3.
若点
P
是反比例函数图象上的一点,过点
P
分别向
x
轴、y
轴作垂线,垂足分别为点
M,N,若四边形
PMON
的面积为
3,则这个反比例函数的关系式是
.
或
例5
如图,P,C是函数
(x>0)
图像上的任意两点,过点
P
作
x
轴的垂线
PA,垂足为
A,过点
C
作
x
轴的
垂线
CD,垂足为
D,连接
OC
交
PA
于点
E.
设
△POA
的面积
为
S1,则
S1=
;梯形CEAD
的面积为
S2,则
S1
与
S2
的大小
关系是
S1
S2;△POE
的面
积
S3
和
S2
的大小关系是S2
S3.
典例精析
2
S1
S2
>
=
S3
如图所示,直线与双曲线交于
A,B
两点,P
是AB
上的点,△
AOC
的面积
S1、△
BOD
的面积
S2、
△
POE
的面积
S3
的大小关系为
.
S1
=
S2
<
S3
练一练
解析:由反比例函数面积的不变
性易知
S1
=
S2.
PE
与双曲线的一
支交于点
F,连接
OF,易知,
S△OFE
=
S1
=
S2,而
S3>S△OFE,
所以
S1,S2,S3的大小关系为
S1
=
S2
<
S3
F
S1
S2
S3
1.
反比例函数
的图象在
(
)
A.
第一、二象限
B.
第一、三象限
C.
第二、三象限
D.第二、四象限
B
巩固练习
2.
在同一直角坐标系中,函数
y
=
2x
与
的
图象大致是
(
)
O
x
y
O
x
y
O
x
y
O
x
y
A.
B.
C.
D.
B
3.
已知反比例函数
的图象在第一、三象
限内,则m的取值范围是________.
4.
下列关于反比例函数
的图象的三个结论:
(1)
经过点
(-1,12)
和点
(10,-1.2);
(2)
在每一个象限内,y
随
x
的增大而减小;
(3)
双曲线位于二、四象限.
其中正确的是
(填序号).
(1)(3)
m
>
2
5.
在反比例函数 (k>0)
的图象上有两点
A
(x1,y1),
B
(x2,y2),
且
x1>x2>0,则
y1-y2
0.
<
y
D
B
A
C
x
6.
如图,点
A
是反比例函数
(x>0)的图象上
任意一点,AB//x
轴交反比例函数
(x<0)
的图象于点
B,以
AB
为边作平行四边形
ABCD,其中
点
C,D
在
x
轴上,则
S平行四边形ABCD
=___.
3
2
5
7.
已知反比例函数
y
=
mxm?-5,它的两个分支分别在
第一、第三象限,求
m
的值.
解:因为反比例函数
y
=
mxm?-5
的两个分支分别在第
一、第三象限,
所以有
m2-5=-1,
m>0,
解得
m=2.
8.
已知反比例函数
的图象经过点
A
(2,-4).
(1)
求
k
的值;
解:∵
反比例函数
的图象经过点
A(2,-4),
∴
把点
A
的坐标代入表达式,得
,
解得
k
=
-8.
(2)
这个函数的图象分布在哪些象限?y
随
x
的增大
如何变化?
解:这个函数的图象位于第二、四象限,在每一个
象限内,y
随
x
的增大而增大.
(3)
画出该函数的图象;
O
x
y
解:如图所示:
(4)
点
B
(1,-8)
,C
(-3,5)是否在该函数的图象上?
因为点
B
的坐标满足该解析式,而点
C
的坐标
不满足该解析式,
所以点
B
在该函数的图象上,点
C
不在该函数
的图象上.
解:该反比例函数的解析式为
.
能力提升:
8.
点
(a-1,y1),(a+1,y2)在反比例函数
(k>0)
的图象上,若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y
随
x
的增大而
减小.
①
当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1,
无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有
y1<0<y2.
∴a-1<0,a+1>0,
解得:-1<a<1.
故
a
的取值范围为:-1<a<1.
反比例函数
(k≠0)
k
k
>
0
k
<
0
图象
性质
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y
随
x
的增大而减小
在每个象限内,y
随
x
的增大而增大
本节小结
第21章
二次函数与反比例函数
沪科版数学九年级上册
第21章
二次函数与反比例函数
沪科版数学九年级上册
21.5
反比例函数
第2课时
反比例函数的图象和性质
学习目标
1.
经历画反比例函数的图象、归纳得到反比例函数的
图象特征和性质的过程
(重点、难点)
2.
会画反比例函数图象,了解和掌握反比例函数的图
象和性质.
(重点)
3.
能够初步应用反比例函数的图象和性质解题.
(重点、
难点)
本节目标
我们已经学习过的函数有哪些?你还记得画这些函数图象时的方法吗?
写出一个反比例函数,你能画出它的图象吗?
引入新知
例1
画反比例函数
与
的图象.
合作探究
提示:画函数的图象步骤一般分为:列表→描点→连线.
需要注意的是在反比例函数中自变量
x
不能为
0.
反比例函数的图象和性质
新知讲解
解:列表如下:
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
…
…
…
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
-2
-2.4
-3
-4
-6
6
4
3
2.4
2
O
-2
描点:以表中各组对应值作为点的坐标,在直角坐标系内描绘出相应的点.
5
6
x
y
4
3
2
1
1
2
3
4
5
6
-3
-4
-1
-5
-6
-1
-2
-3
-4
-5
-6
连线:用光滑的曲线顺次连接各点,即可
得
的图象.
观察这两个函数图象,回答问题:
思考:
(1)
每个函数图象分别位于哪些象限?
(2)
在每一个象限内,随着x的增大,y如何变化?
你能由它们的解析式说明理由吗?
(3)
对于反比例函数
(k>0),考虑问题(1)(2),
你能得出同样的结论吗?
●由两条曲线组成,且分别位于第一、三象限
它们与
x
轴、y
轴都不相交;
●在每个象限内,y
随
x
的增大而减小.
反比例函数
(k>0)
的图象和性质:
1.
反比例函数
的图象大致是
(
)
C
y
A.
x
y
o
B.
x
o
D.
x
y
o
C.
x
y
o
练一练
2.
已知反比例函数
的图象过点(-2,-3),函
数图象上有两点
A(
,y1),B(5,y2),则
y1与y2
的大小关系为
(
)
A.
y1
>
y2
B.
y1
=
y2
C.
y1
<
y2
D.
无法确定
C
提示:由题可知反比例函数的解析式为
,因为6>0,且
A,B
两点均在该函数图象的第一象限部分,根据
>5,可知y1,y2的大小关系.
观察与思考
当
k
=-2,-4,-6时,反比例函数
的图象,有哪些共同特征?回顾上面我们利用函数图象,从特殊到一般研究反比例函数
(k>0)
的性质的过程,你能用类似的方法研究反比例函数
(k<0)的图象和性质吗?
y
x
O
y
x
O
y
x
O
反比例函数
(k<0)
的图象和性质:
●由两条曲线组成,且分别位于第二、四象限
它们与x轴、y轴都不相交;
●在每个象限内,y随x的增大而增大.
归纳:
(1)
当
k
>
0
时,双曲线的两支分别位于第一、三
象限,在每一象限内,y
随
x
的增大而减小;
(2)
当
k
<
0
时,双曲线的两支分别位于第二、四
象限,在每一象限内,y
随
x
的增大而增大.
一般地,反比例函数
的图象是双曲线,它具有以下性质:
k
的正负决定反比例函数所在的象限和增减性
点(2,y1)和(3,y2)在函数
上,则y1
y2
(填“>”“<”或“=”).
<
练一练
例2
已知反比例函数
,y
随
x
的增大而增大,求a的值.
解:由题意得a2+a-7=-1,且a-1<0.
解得
a=-3.
反比例函数的图象和性质的初步运用
练一练
已知反比例函数
在每个象限内,y
随着
x
的增大而减小,求
m
的值.
解:由题意得
m2-10=-1,且
3m-8>0.
解得
m=3.
例3
已知反比例函数的图象经过点
A
(2,6).
(1)
这个函数的图象位于哪些象限?y
随
x
的增大如
何变化?
解:因为点
A
(2,6)
在第一象限,所以这个函数的
图象位于第一、三象限;
在每一个象限内,y
随
x
的增大而减小.
(2)
点B(3,4),C(
,
),D(2,5)是否在这个
函数的图象上?
解:设这个反比例函数的解析式为
,因为点
A
(2,6)在其图象上,所以有
,解得
k
=12.
因为点
B,C
的坐标都满足该解析式,而点
D的坐标不满足,所以点
B,C
在这个函数的图象上,点
D
不在这个函数的图象上.
所以反比例函数的解析式为
.
(1)
图象的另一支位于哪个象限?常数
m
的取值范围
是什么?
O
x
y
例4
如图,是反比例函数
图象的一支.
根据图象,回答下列问题:
解:因为这个反比例函数图象的一
支位于第一象限,所以另一支
必位于第三象限.
由因为这个函数图象位于第一、
三象限,所以m-5>0,
解得m>5.
(2)
在这个函数图象的某一支上任取点
A
(x1,y1)
和
点B
(x2,y2).
如果x1>x2,那么
y1
和
y2
有怎样的
大小关系?
解:因为
m-5
>
0,所以在这个函数图象的任一支
上,y
都随
x
的增大而减小,因此当x1>x2时,
y1<y2.
(1)
如果这个函数图象经过点(-3,5),求k的值;
(2)如果这个函数图象在它所处的象限内,函数y随x的增大而减小,求k的范围.
例5
已知反比例函数
解:(1)
因为函数图象经过点(-3,5),代入
函数的表达式,得
解方程,得k=-7.
(2)根据题意,有2k-1>0.
解不等式,得
1.
在反比例函数
的图象上分别取点P,Q
向
x
轴、y
轴作垂线,围成面积分别为S1,S2的矩形,
填写下页表格:
合作探究
反比例函数解析式中
k
的几何意义
5
1
2
3
4
-1
5
x
y
O
P
S1
S2
P
(2,2)
Q
(4,1)
S1的值
S2的值
S1与S2的关系
猜想
S1,S2
与
k的关系
4
4
S1=S2
S1=S2=k
-5
-4
-3
-2
1
4
3
2
-3
-2
-4
-5
-1
Q
S1的值
S2的值
S1与S2的关系
猜想与
k
的关系
P
(-1,4)
Q
(-2,2)
2.
若在反比例函数
中也
用同样的方法分别取
P,Q
两点,填写表格:
4
4
S1=S2
S1=S2=-k
y
x
O
P
Q
S1
S2
由前面的探究过程,可以猜想:
若点P是
图象上的任意一点,作
PA
垂直于
x
轴,作
PB
垂直于
y
轴,矩形
AOBP
的面积与k
的关系是S矩形
AOBP=|k|.
y
x
O
P
S
我们就
k
<
0
的情况给出证明:
设点
P
的坐标为
(a,b)
A
B
∵点
P
(a,b)
在函数
的图
象上,
∴
,即
ab=k.
∴
S矩形
AOBP=PB·PA=-a·b=-ab=-k;
若点
P
在第二象限,则
a<0,b>0,
若点
P
在第四象限,则
a>0,b<0,
∴
S矩形
AOBP=PB·PA
=a·
(-b)=-ab=-k.
B
P
A
综上,S矩形
AOBP=|k|.
自己尝试证明
k
>
0的情况.
点
Q
是其图象上的任意一
点,作
QA
垂直于
y
轴,作
QB
垂直于x
轴,矩形AOBQ
的面积与
k
的关系是
S矩形AOBQ=
.
推理:△QAO与△QBO的
面积和
k
的关系是
S△QAO=S△QBO=
.
Q
对于反比例函数
,
A
B
|k|
y
x
O
归纳:
反比例函数的面积不变性
A.
SA
>SB>SC
B.
SA
SA
=SB=SC
D.
SA
如图,在函数
(x>0)的图像上有三点A,B
,
C,过这三点分别向
x
轴、y
轴作垂线,过每一点
所作的两条垂线与x轴、
y轴围成的矩形的面积分
别为SA
,SB,SC,则
(
)
y
x
O
A
B
C
C
练一练
2.
如图,过反比例函数
图象上的一点
P,作
PA⊥x
轴于A.
若△POA
的面积为
6,则
k
=
.
-12
提示:当反比例函数图象在第二、四象限时,注意
k<0.
y
x
O
P
A
3.
若点
P
是反比例函数图象上的一点,过点
P
分别向
x
轴、y
轴作垂线,垂足分别为点
M,N,若四边形
PMON
的面积为
3,则这个反比例函数的关系式是
.
或
例5
如图,P,C是函数
(x>0)
图像上的任意两点,过点
P
作
x
轴的垂线
PA,垂足为
A,过点
C
作
x
轴的
垂线
CD,垂足为
D,连接
OC
交
PA
于点
E.
设
△POA
的面积
为
S1,则
S1=
;梯形CEAD
的面积为
S2,则
S1
与
S2
的大小
关系是
S1
S2;△POE
的面
积
S3
和
S2
的大小关系是S2
S3.
典例精析
2
S1
S2
>
=
S3
如图所示,直线与双曲线交于
A,B
两点,P
是AB
上的点,△
AOC
的面积
S1、△
BOD
的面积
S2、
△
POE
的面积
S3
的大小关系为
.
S1
=
S2
<
S3
练一练
解析:由反比例函数面积的不变
性易知
S1
=
S2.
PE
与双曲线的一
支交于点
F,连接
OF,易知,
S△OFE
=
S1
=
S2,而
S3>S△OFE,
所以
S1,S2,S3的大小关系为
S1
=
S2
<
S3
F
S1
S2
S3
1.
反比例函数
的图象在
(
)
A.
第一、二象限
B.
第一、三象限
C.
第二、三象限
D.第二、四象限
B
巩固练习
2.
在同一直角坐标系中,函数
y
=
2x
与
的
图象大致是
(
)
O
x
y
O
x
y
O
x
y
O
x
y
A.
B.
C.
D.
B
3.
已知反比例函数
的图象在第一、三象
限内,则m的取值范围是________.
4.
下列关于反比例函数
的图象的三个结论:
(1)
经过点
(-1,12)
和点
(10,-1.2);
(2)
在每一个象限内,y
随
x
的增大而减小;
(3)
双曲线位于二、四象限.
其中正确的是
(填序号).
(1)(3)
m
>
2
5.
在反比例函数 (k>0)
的图象上有两点
A
(x1,y1),
B
(x2,y2),
且
x1>x2>0,则
y1-y2
0.
<
y
D
B
A
C
x
6.
如图,点
A
是反比例函数
(x>0)的图象上
任意一点,AB//x
轴交反比例函数
(x<0)
的图象于点
B,以
AB
为边作平行四边形
ABCD,其中
点
C,D
在
x
轴上,则
S平行四边形ABCD
=___.
3
2
5
7.
已知反比例函数
y
=
mxm?-5,它的两个分支分别在
第一、第三象限,求
m
的值.
解:因为反比例函数
y
=
mxm?-5
的两个分支分别在第
一、第三象限,
所以有
m2-5=-1,
m>0,
解得
m=2.
8.
已知反比例函数
的图象经过点
A
(2,-4).
(1)
求
k
的值;
解:∵
反比例函数
的图象经过点
A(2,-4),
∴
把点
A
的坐标代入表达式,得
,
解得
k
=
-8.
(2)
这个函数的图象分布在哪些象限?y
随
x
的增大
如何变化?
解:这个函数的图象位于第二、四象限,在每一个
象限内,y
随
x
的增大而增大.
(3)
画出该函数的图象;
O
x
y
解:如图所示:
(4)
点
B
(1,-8)
,C
(-3,5)是否在该函数的图象上?
因为点
B
的坐标满足该解析式,而点
C
的坐标
不满足该解析式,
所以点
B
在该函数的图象上,点
C
不在该函数
的图象上.
解:该反比例函数的解析式为
.
能力提升:
8.
点
(a-1,y1),(a+1,y2)在反比例函数
(k>0)
的图象上,若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y
随
x
的增大而
减小.
①
当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1,
无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有
y1<0<y2.
∴a-1<0,a+1>0,
解得:-1<a<1.
故
a
的取值范围为:-1<a<1.
反比例函数
(k≠0)
k
k
>
0
k
<
0
图象
性质
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y
随
x
的增大而减小
在每个象限内,y
随
x
的增大而增大
本节小结
第21章
二次函数与反比例函数
沪科版数学九年级上册
