沪科版数学九年级上册22.2 第1课时 平行线与相似三角形课件(23张)
文档属性
| 名称 | 沪科版数学九年级上册22.2 第1课时 平行线与相似三角形课件(23张) |
|
|
| 格式 | zip | ||
| 文件大小 | 659.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第22章
相似形
沪科版数学九年级上册
22.2
相似三角形的判定
第1课时
平行线与相似三角形
1.理解相似三角形的定义,掌握定义中的两个条件;
(重点)
2.会用平行线判定两个三角形相似并进行证明和计算.
(难点)
学习目标
本节目标
问题1
相似多边形的主要特征是什么?
问题2
相似比的定义是什么?
引入新知
问题思考
我们就说△ABC与△A′B′C′______,记作__________________,△ABC与△A′B′C′相似比是k,则△A′B′C′与△ABC的相似比是____.
在相似多边形中,最简单的就是相似三角形.
在△ABC与△A′B′C′中,如果∠A=∠A′,
∠B=∠B′,
∠C=∠C′,
△ABC∽△A′B′C′
相似
相似三角形的性质及有关概念
新知讲解
反之如果△ABC∽△A′B′C′,则有∠A=_____,∠B=_____,∠C=____,
且
∠A′
∠B′
∠C′
相似比为1时,相似的
两个图形有什么关系?
当相似比等于1时,相似图形是全等图形,全等是一种特殊的相似.
例1
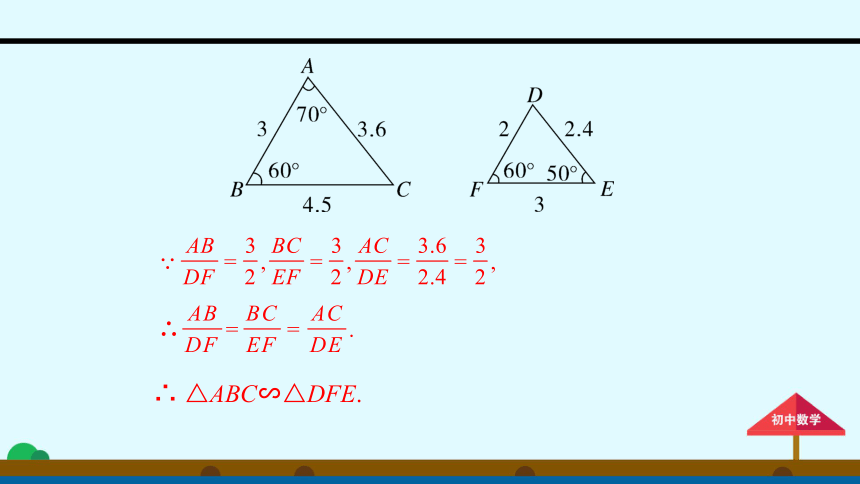
△ABC与△DEF的各角度数和边长如图所示,则△ABC与△DEF能否相似?说明理由.
解:因为∠A=70°,∠B=60°,所以∠C=50°.
因为∠F=60°,∠E=50°,所以∠D=70°.
所以∠A=∠D,∠B=∠F,∠C=∠E.
典例精析
∴
△ABC∽△DFE.
判断两个三角形相似,一定要具备两个条件:一是对应角相等,二是对应边成比例.另外在书写两个三角形相似时,一定要将对应的顶点写在对应的位置上.
归纳总结
例2
如图,已知△ABC∽△ADE,AE=50cm,EC=30cm,BC=58cm,∠BAC=45°,∠ACB=40°,求:
(1)∠AED和∠ADE的度数;
(2)DE的长.
解:(1)∵△ABC∽△ADE,
∴∠AED=∠ACB=40°.
在△ADE中,∠ADE=180°-40°-45°=95°;
(2)
∵△ABC∽△DFE.
∴DE=36.25(cm).
当题目中有相似三角形(或能证明出相似三角形)时,首先考虑用相似三角形的性质,由性质既能得到相等的角,又能得到成比例的线段.
归纳总结
如图,DE//BC,
△ADE与△ABC有什么关系?说明理由.
A
B
C
D
解:相似,在△ADE与△ABC中,
∠A=
∠A.
∵
DE//BC,
∴∠ADE=∠B,
∠AED=∠C,
过E作EF//AB交BC于F,
F
E
平行线与相似三角形
探究归纳
∵DBFE是平行四边形,
∴DE=BF.
∴△ADE∽△ABC
A
B
C
D
F
E
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
“A”型
“X”型
(图3)
D
E
O
B
C
A
B
C
D
E
(图1)
“A”型
A
D
E
B
C
(图2)
归纳总结
例3
如图,已知在平行四边形ABCD中,E为AB延长线上一点,AB=3BE,DE与BC相交于点F.请找出图中各对相似三角形,并求出相应的相似比.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△BEF∽△CDF,△BEF∽△AED,
∴△BEF∽△CDF∽△AED.
故当△BEF∽△CDF时,
相似比为BE:
CD=BE:
AB=1:3;
当△BEF∽△AED时,相似比为BE:
AE=1:4;
当△CDF∽△AED时,相似比为CD:
AE=3:4.
例4
已知:如图是一束光线射入室内的平面图,上檐边缘射入的光线照在距窗户2.5m处,已知窗户AB高为2m,B点距地面高为1.2m,求下檐光线的落地点N与窗户的距离NC.
解:∵AM∥BN,
∴△NBC∽△MAC,
A
B
C
D
E
相似具有传递性
△ADE∽△ABC
M
N
如果再作
MN∥DE
,共有多少对相似三角形?
△AMN∽△ADE
△AMN∽△ABC
共有三对相似三角形
已知DE∥BC
合作交流
如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
随堂练习
1.如果两个三角形的相似比为1,那么这两个三
角形_____.
2.若△ABC与△A′B′C′相似,一组对应边的长为
AB=3
cm,A′B′=
4
cm,那么△A′B′C′与△ABC的
相似比是____
.
3.若△ABC的三条边长分别为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12
cm,那么△
A′B′C′的最大边长是_____.
全等
4︰3
24cm
巩固练习
4.已知△ABC的三条边长3cm,4cm,5cm,
△ABC∽△A1B1C1,那么△A1B1C1的形状是__________,又知△A1B1C1的最大边长为25cm,那么△A1B1C1的面积为________.
直角三角形
150cm2
5.若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那
么∠
C′的度数是(
)
A.55°
B.100°
C.25°
D.不能确定
C
6.把△ABC的各边分别扩大为原来的3倍,得到△A′B′C′,下列结论不能成立的是(
)
A.△ABC∽△A′B′C′
B.△ABC与△A′B′C′的各对应角相等
C.△ABC与△A′B′C′的相似比为
D.△ABC与△A′B′C′的相似比为
C
2.当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似;
3.平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
1.相似三角形的对应边成比例,对应角相等,相似
比等于对应边的比;
本节小结
第22章
相似形
沪科版数学九年级上册
第22章
相似形
沪科版数学九年级上册
22.2
相似三角形的判定
第1课时
平行线与相似三角形
1.理解相似三角形的定义,掌握定义中的两个条件;
(重点)
2.会用平行线判定两个三角形相似并进行证明和计算.
(难点)
学习目标
本节目标
问题1
相似多边形的主要特征是什么?
问题2
相似比的定义是什么?
引入新知
问题思考
我们就说△ABC与△A′B′C′______,记作__________________,△ABC与△A′B′C′相似比是k,则△A′B′C′与△ABC的相似比是____.
在相似多边形中,最简单的就是相似三角形.
在△ABC与△A′B′C′中,如果∠A=∠A′,
∠B=∠B′,
∠C=∠C′,
△ABC∽△A′B′C′
相似
相似三角形的性质及有关概念
新知讲解
反之如果△ABC∽△A′B′C′,则有∠A=_____,∠B=_____,∠C=____,
且
∠A′
∠B′
∠C′
相似比为1时,相似的
两个图形有什么关系?
当相似比等于1时,相似图形是全等图形,全等是一种特殊的相似.
例1
△ABC与△DEF的各角度数和边长如图所示,则△ABC与△DEF能否相似?说明理由.
解:因为∠A=70°,∠B=60°,所以∠C=50°.
因为∠F=60°,∠E=50°,所以∠D=70°.
所以∠A=∠D,∠B=∠F,∠C=∠E.
典例精析
∴
△ABC∽△DFE.
判断两个三角形相似,一定要具备两个条件:一是对应角相等,二是对应边成比例.另外在书写两个三角形相似时,一定要将对应的顶点写在对应的位置上.
归纳总结
例2
如图,已知△ABC∽△ADE,AE=50cm,EC=30cm,BC=58cm,∠BAC=45°,∠ACB=40°,求:
(1)∠AED和∠ADE的度数;
(2)DE的长.
解:(1)∵△ABC∽△ADE,
∴∠AED=∠ACB=40°.
在△ADE中,∠ADE=180°-40°-45°=95°;
(2)
∵△ABC∽△DFE.
∴DE=36.25(cm).
当题目中有相似三角形(或能证明出相似三角形)时,首先考虑用相似三角形的性质,由性质既能得到相等的角,又能得到成比例的线段.
归纳总结
如图,DE//BC,
△ADE与△ABC有什么关系?说明理由.
A
B
C
D
解:相似,在△ADE与△ABC中,
∠A=
∠A.
∵
DE//BC,
∴∠ADE=∠B,
∠AED=∠C,
过E作EF//AB交BC于F,
F
E
平行线与相似三角形
探究归纳
∵DBFE是平行四边形,
∴DE=BF.
∴△ADE∽△ABC
A
B
C
D
F
E
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
“A”型
“X”型
(图3)
D
E
O
B
C
A
B
C
D
E
(图1)
“A”型
A
D
E
B
C
(图2)
归纳总结
例3
如图,已知在平行四边形ABCD中,E为AB延长线上一点,AB=3BE,DE与BC相交于点F.请找出图中各对相似三角形,并求出相应的相似比.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△BEF∽△CDF,△BEF∽△AED,
∴△BEF∽△CDF∽△AED.
故当△BEF∽△CDF时,
相似比为BE:
CD=BE:
AB=1:3;
当△BEF∽△AED时,相似比为BE:
AE=1:4;
当△CDF∽△AED时,相似比为CD:
AE=3:4.
例4
已知:如图是一束光线射入室内的平面图,上檐边缘射入的光线照在距窗户2.5m处,已知窗户AB高为2m,B点距地面高为1.2m,求下檐光线的落地点N与窗户的距离NC.
解:∵AM∥BN,
∴△NBC∽△MAC,
A
B
C
D
E
相似具有传递性
△ADE∽△ABC
M
N
如果再作
MN∥DE
,共有多少对相似三角形?
△AMN∽△ADE
△AMN∽△ABC
共有三对相似三角形
已知DE∥BC
合作交流
如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
随堂练习
1.如果两个三角形的相似比为1,那么这两个三
角形_____.
2.若△ABC与△A′B′C′相似,一组对应边的长为
AB=3
cm,A′B′=
4
cm,那么△A′B′C′与△ABC的
相似比是____
.
3.若△ABC的三条边长分别为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12
cm,那么△
A′B′C′的最大边长是_____.
全等
4︰3
24cm
巩固练习
4.已知△ABC的三条边长3cm,4cm,5cm,
△ABC∽△A1B1C1,那么△A1B1C1的形状是__________,又知△A1B1C1的最大边长为25cm,那么△A1B1C1的面积为________.
直角三角形
150cm2
5.若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那
么∠
C′的度数是(
)
A.55°
B.100°
C.25°
D.不能确定
C
6.把△ABC的各边分别扩大为原来的3倍,得到△A′B′C′,下列结论不能成立的是(
)
A.△ABC∽△A′B′C′
B.△ABC与△A′B′C′的各对应角相等
C.△ABC与△A′B′C′的相似比为
D.△ABC与△A′B′C′的相似比为
C
2.当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似;
3.平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
1.相似三角形的对应边成比例,对应角相等,相似
比等于对应边的比;
本节小结
第22章
相似形
沪科版数学九年级上册
