沪科版数学九年级上册22.2 第3课时 相似三角形的判定定理2课件(23张)
文档属性
| 名称 | 沪科版数学九年级上册22.2 第3课时 相似三角形的判定定理2课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 701.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 00:00:00 | ||
图片预览




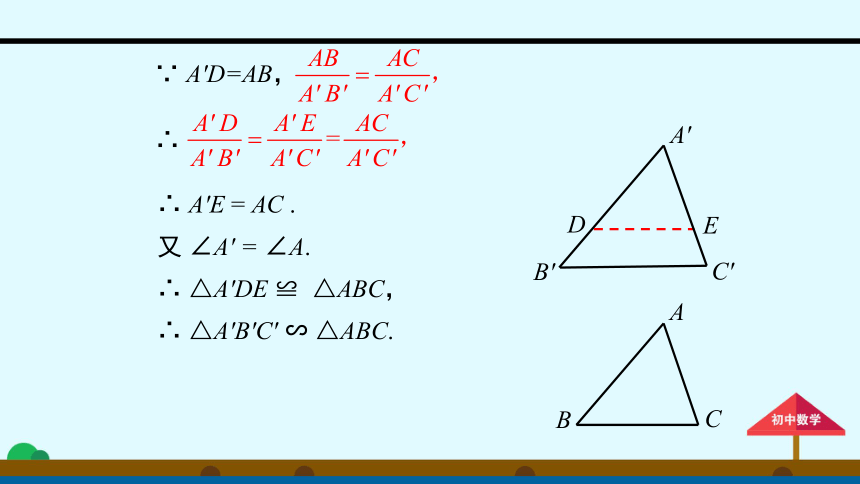


文档简介
(共23张PPT)
第22章
相似形
沪科版数学九年级上册
22.2
相似三角形的判定
第3课时
相似三角形的判定定理2
学习目标
1.掌握相似三角形的判定定理2;(重点)
2.能熟练运用相似三角形的判定定理2.(难点)
本节目标
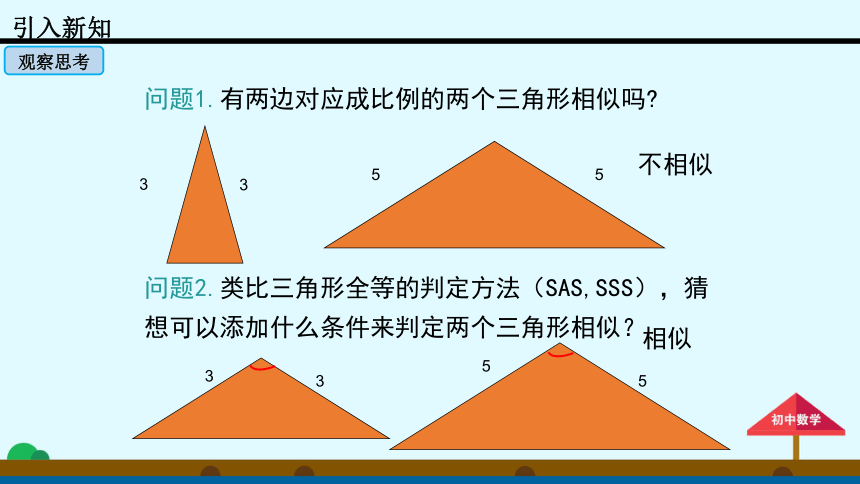
问题1.有两边对应成比例的两个三角形相似吗?
3
3
5
5
不相似
问题2.类比三角形全等的判定方法(SAS,SSS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
相似
引入新知
观察思考
利用刻度尺和量角器画
△ABC和
△A′B′C′,使
∠A=∠A′,
量出
BC
及
B′C′
的长,
它们的比值等于
k
吗?再量一量两个三角形另外的
两个角,你有什么发现?△ABC
与
△A′B′C′
有何关
系?
两个三角形相似
改变
k
和∠A
的值的大小,是否有同样的结论?
引入新知
两边成比例且夹角相等的两个三角形相似
合作探究
我们来证明一下前面得出的结论:
如图,在△ABC与△A′B′C′中,已知∠A=
∠A′,
证明:
在
△A′B′C′
的边
A′B′
上截取点D,
使
A′D
=
AB.过点
D
作
DE∥B′C′,
交
A′C′
于点
E.
∵
DE∥B′C′,
∴
△A′DE∽△A′B′C′.
求证:△ABC∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∴
∴
A′E
=
AC
.
又
∠A′
=
∠A.
∴
△A′DE
≌
△ABC,
∴
△A′B′C′
∽
△ABC.
B
A
C
D
E
B'
A'
C'
∵
A′D=AB,
∴
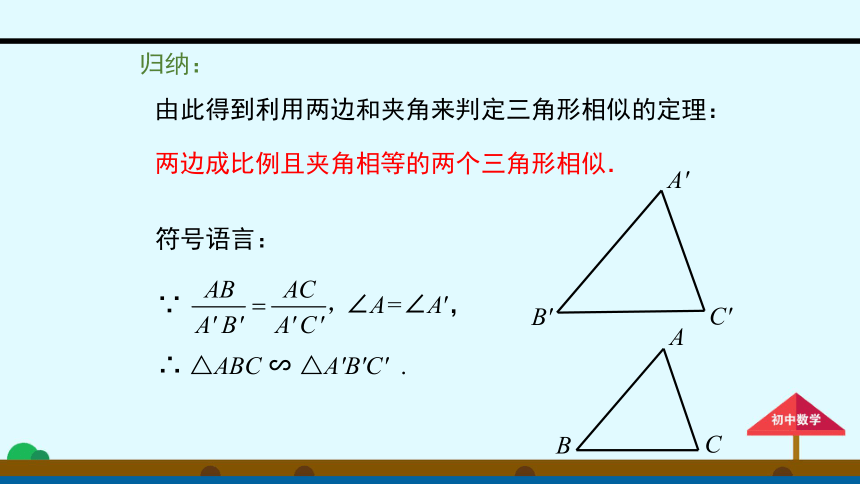
由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言:
∵
∠A=∠A′,
B
A
C
B'
A'
C'
∴
△ABC
∽
△A′B′C′
.
归纳:
对于△ABC和
△A′B′C′,如果
A′B′
:
AB=
A′C′
:
AC.
∠B=
∠B′,这两个三角形一定会相似吗?
不会,如下图,因为不能证明构造的三角形和原三角形全等.
A
B
C
思考:
A′
B′
B″
C′
结论:
如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角.
例1
根据下列条件,判断
△ABC
和
△A′B′C′
是否相似,并说明理由:
(1)AB=5,AC=3
,∠A=45°,A'B'=10,A'C'=6,
∠A=45°;
解:(1)∵
∴
又
∠A′
=
∠A=45°,∴
△ABC
∽
△A′B′C′.
典例精析
(2)∠A=38°,∠C=97°,∠A'=38°,∠B'=45°
.
解:(2)∵∠B=180°-
∠A-∠C=45°
∴∠B=∠B'=45°.
又
∠A′
=
∠A=38°,
∴
△ABC
∽
△A′B′C′.
1.
在
△ABC
和
△DEF
中,∠C
=∠F=70°,AC
=
3.5
cm,BC
=
2.5
cm,DF
=2.1
cm,EF
=1.5
cm.
求证:△DEF∽△ABC.
A
C
B
F
E
D
证明:
∵
AC
=
3.5
cm,BC
=
2.5
cm,
DF
=
2.1
cm,EF
=
1.5
cm,
又
∵∠C
=∠F
=
70°,∴
△DEF
∽△ABC.
∴
随堂练习
2.
如图,△ABC
与
△ADE
都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.
求证:△ABC
∽△ADE.
证明:
∵
△ABC
与
△ADE
是等腰三角形,
∴
AD
=AE,AB
=
AC,
∴
又
∵∠DAB
=
∠CAE,
∴
∠DAB
+∠BAE
=
∠CAE
+∠BAE,
即
∠DAE
=∠BAC,∴△ABC
∽
△ADE.
A
B
C
D
E
解:∵
AE=1.5,AC=2,
例2
如图,D,E分别是
△ABC
的边
AC,AB
上的点,
AE=1.5,AC=2,BC=3,且
,求
DE
的长.
A
C
B
E
D
∴
又∵∠EAD=∠CAB,
∴
△ADE
∽△ABC,
∴
∴
提示:解题时要找准对应边.
证明:
∵
CD
是边
AB
上的高,
∴
∠ADC
=∠CDB
=90°.
∴△ADC
∽△CDB,∴
∠ACD
=∠B,
∴
∠ACB
=∠ACD
+∠BCD
=∠B
+∠BCD
=
90°.
例3
如图,在
△ABC
中,CD
是边
AB
上的高,且
,求证
∠ACB=90°.
A
B
C
D
∵
方法总结:解题时需注意隐含条件,如垂直关系,三角形的高等.
1.
判断
(1)
两个等边三角形相似
(
)
(2)
两个直角三角形相似
(
)
(3)
两个等腰直角三角形相似
(
)
(4)
有一个角是50°的两个等腰三角形相似
(
)
×
√
√
×
巩固练习
2.
如图,D
是
△ABC
一边
BC
上一点,连接
AD,使
△ABC
∽
△DBA的条件是
(
)
A.
AC
:
BC=AD
:
BD
B.
AC
:
BC=AB
:
AD
C.
AB2
=
CD
·
BC
D.
AB2
=
BD
·
BC
D
A
B
C
D
3.
如图
△AEB
和
△FEC
(填
“相似”
或
“不相似”)
.
54
30
36
45
E
A
F
C
B
1
2
相似
解析:当
△ADP
∽△ACB
时,
AP
:
AB
=AD
:
AC
,∴
AP
:
12
=6
:
8
,
解得
AP
=
9;
当
△ADP
∽△ABC
时,
AD
:
AB
=AP
:
AC
,∴
6
:
12
=
AP
:
8
,
解得
AP
=
4.
∴
当
AP
的长度为
4
或
9
时,
△ADP
和
△ABC
相似.
4.
如图,已知
△ABC中,D
为边
AC
上一点,P
为边
AB上一点,AB
=
12,AC
=
8,AD
=
6,当
AP
的长
度为
时,△ADP
和
△ABC
相似.
A
B
C
D
4
或
9
P
P
5.
如图,在四边形
ABCD
中,已知
∠B
=∠ACD,
AB=6,BC=4,AC=5,CD=
,求
AD
的长.
A
B
C
D
解:∵AB=6,BC=4,AC=5,CD=
,
∴
又∵∠B=∠ACD,
∴
△ABC
∽
△DCA,
∴
,
∴
6.
如图,∠DAB
=∠CAE,且
AB
·
AD
=
AE·AC,求证
△ABC
∽△AED.
A
B
C
D
E
证明:∵
AB
·
AD
=
AE·AC,
∴
又∵
∠DAB
=∠CAE,
∴∠
DAB
+∠BAE
=∠CAE
+∠BAE
,
即∠DAE
=∠BAC,
∴
△ABC
∽△AED.
两边成比例且夹角相等的两个三角形相似
利用两边及夹角判定三角形相似
相似三角形的判定定理的运用
本节小结
第22章
相似形
沪科版数学九年级上册
第22章
相似形
沪科版数学九年级上册
22.2
相似三角形的判定
第3课时
相似三角形的判定定理2
学习目标
1.掌握相似三角形的判定定理2;(重点)
2.能熟练运用相似三角形的判定定理2.(难点)
本节目标
问题1.有两边对应成比例的两个三角形相似吗?
3
3
5
5
不相似
问题2.类比三角形全等的判定方法(SAS,SSS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
相似
引入新知
观察思考
利用刻度尺和量角器画
△ABC和
△A′B′C′,使
∠A=∠A′,
量出
BC
及
B′C′
的长,
它们的比值等于
k
吗?再量一量两个三角形另外的
两个角,你有什么发现?△ABC
与
△A′B′C′
有何关
系?
两个三角形相似
改变
k
和∠A
的值的大小,是否有同样的结论?
引入新知
两边成比例且夹角相等的两个三角形相似
合作探究
我们来证明一下前面得出的结论:
如图,在△ABC与△A′B′C′中,已知∠A=
∠A′,
证明:
在
△A′B′C′
的边
A′B′
上截取点D,
使
A′D
=
AB.过点
D
作
DE∥B′C′,
交
A′C′
于点
E.
∵
DE∥B′C′,
∴
△A′DE∽△A′B′C′.
求证:△ABC∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∴
∴
A′E
=
AC
.
又
∠A′
=
∠A.
∴
△A′DE
≌
△ABC,
∴
△A′B′C′
∽
△ABC.
B
A
C
D
E
B'
A'
C'
∵
A′D=AB,
∴
由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言:
∵
∠A=∠A′,
B
A
C
B'
A'
C'
∴
△ABC
∽
△A′B′C′
.
归纳:
对于△ABC和
△A′B′C′,如果
A′B′
:
AB=
A′C′
:
AC.
∠B=
∠B′,这两个三角形一定会相似吗?
不会,如下图,因为不能证明构造的三角形和原三角形全等.
A
B
C
思考:
A′
B′
B″
C′
结论:
如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角.
例1
根据下列条件,判断
△ABC
和
△A′B′C′
是否相似,并说明理由:
(1)AB=5,AC=3
,∠A=45°,A'B'=10,A'C'=6,
∠A=45°;
解:(1)∵
∴
又
∠A′
=
∠A=45°,∴
△ABC
∽
△A′B′C′.
典例精析
(2)∠A=38°,∠C=97°,∠A'=38°,∠B'=45°
.
解:(2)∵∠B=180°-
∠A-∠C=45°
∴∠B=∠B'=45°.
又
∠A′
=
∠A=38°,
∴
△ABC
∽
△A′B′C′.
1.
在
△ABC
和
△DEF
中,∠C
=∠F=70°,AC
=
3.5
cm,BC
=
2.5
cm,DF
=2.1
cm,EF
=1.5
cm.
求证:△DEF∽△ABC.
A
C
B
F
E
D
证明:
∵
AC
=
3.5
cm,BC
=
2.5
cm,
DF
=
2.1
cm,EF
=
1.5
cm,
又
∵∠C
=∠F
=
70°,∴
△DEF
∽△ABC.
∴
随堂练习
2.
如图,△ABC
与
△ADE
都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.
求证:△ABC
∽△ADE.
证明:
∵
△ABC
与
△ADE
是等腰三角形,
∴
AD
=AE,AB
=
AC,
∴
又
∵∠DAB
=
∠CAE,
∴
∠DAB
+∠BAE
=
∠CAE
+∠BAE,
即
∠DAE
=∠BAC,∴△ABC
∽
△ADE.
A
B
C
D
E
解:∵
AE=1.5,AC=2,
例2
如图,D,E分别是
△ABC
的边
AC,AB
上的点,
AE=1.5,AC=2,BC=3,且
,求
DE
的长.
A
C
B
E
D
∴
又∵∠EAD=∠CAB,
∴
△ADE
∽△ABC,
∴
∴
提示:解题时要找准对应边.
证明:
∵
CD
是边
AB
上的高,
∴
∠ADC
=∠CDB
=90°.
∴△ADC
∽△CDB,∴
∠ACD
=∠B,
∴
∠ACB
=∠ACD
+∠BCD
=∠B
+∠BCD
=
90°.
例3
如图,在
△ABC
中,CD
是边
AB
上的高,且
,求证
∠ACB=90°.
A
B
C
D
∵
方法总结:解题时需注意隐含条件,如垂直关系,三角形的高等.
1.
判断
(1)
两个等边三角形相似
(
)
(2)
两个直角三角形相似
(
)
(3)
两个等腰直角三角形相似
(
)
(4)
有一个角是50°的两个等腰三角形相似
(
)
×
√
√
×
巩固练习
2.
如图,D
是
△ABC
一边
BC
上一点,连接
AD,使
△ABC
∽
△DBA的条件是
(
)
A.
AC
:
BC=AD
:
BD
B.
AC
:
BC=AB
:
AD
C.
AB2
=
CD
·
BC
D.
AB2
=
BD
·
BC
D
A
B
C
D
3.
如图
△AEB
和
△FEC
(填
“相似”
或
“不相似”)
.
54
30
36
45
E
A
F
C
B
1
2
相似
解析:当
△ADP
∽△ACB
时,
AP
:
AB
=AD
:
AC
,∴
AP
:
12
=6
:
8
,
解得
AP
=
9;
当
△ADP
∽△ABC
时,
AD
:
AB
=AP
:
AC
,∴
6
:
12
=
AP
:
8
,
解得
AP
=
4.
∴
当
AP
的长度为
4
或
9
时,
△ADP
和
△ABC
相似.
4.
如图,已知
△ABC中,D
为边
AC
上一点,P
为边
AB上一点,AB
=
12,AC
=
8,AD
=
6,当
AP
的长
度为
时,△ADP
和
△ABC
相似.
A
B
C
D
4
或
9
P
P
5.
如图,在四边形
ABCD
中,已知
∠B
=∠ACD,
AB=6,BC=4,AC=5,CD=
,求
AD
的长.
A
B
C
D
解:∵AB=6,BC=4,AC=5,CD=
,
∴
又∵∠B=∠ACD,
∴
△ABC
∽
△DCA,
∴
,
∴
6.
如图,∠DAB
=∠CAE,且
AB
·
AD
=
AE·AC,求证
△ABC
∽△AED.
A
B
C
D
E
证明:∵
AB
·
AD
=
AE·AC,
∴
又∵
∠DAB
=∠CAE,
∴∠
DAB
+∠BAE
=∠CAE
+∠BAE
,
即∠DAE
=∠BAC,
∴
△ABC
∽△AED.
两边成比例且夹角相等的两个三角形相似
利用两边及夹角判定三角形相似
相似三角形的判定定理的运用
本节小结
第22章
相似形
沪科版数学九年级上册
