沪科版数学九年级上册22.2 第5课时 判定两个直角三角形相似课件(19张)
文档属性
| 名称 | 沪科版数学九年级上册22.2 第5课时 判定两个直角三角形相似课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 850.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 08:37:19 | ||
图片预览




文档简介
(共19张PPT)
第22章
相似形
沪科版数学九年级上册
22.2
相似三角形的判定
第5课时
判定两个直角三角形相似
1.掌握直角三角形相似的判定;(重点)
2.能熟练地运用直角三角形相似的判定定理.(难点)
学习目标
本节目标
观察两副三角尺如图,其中同样角度(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.一般地,如果两个三角形有两组对应角相等,它们一定相似吗?对于直角三角形,类似于判定三角形全等的HL方法,我们能不能通过两边来判断两个三角形相似呢?
引入新知
观察思考
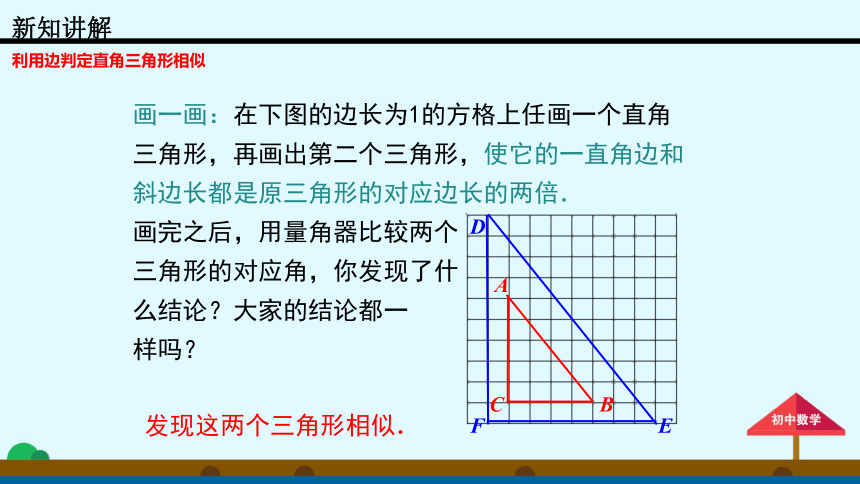
画一画:在下图的边长为1的方格上任画一个直角三角形,再画出第二个三角形,使它的一直角边和斜边长都是原三角形的对应边长的两倍.
画完之后,用量角器比较两个
三角形的对应角,你发现了什
么结论?大家的结论都一
样吗?
B
C
A
F
E
D
发现这两个三角形相似.
利用边判定直角三角形相似
新知讲解
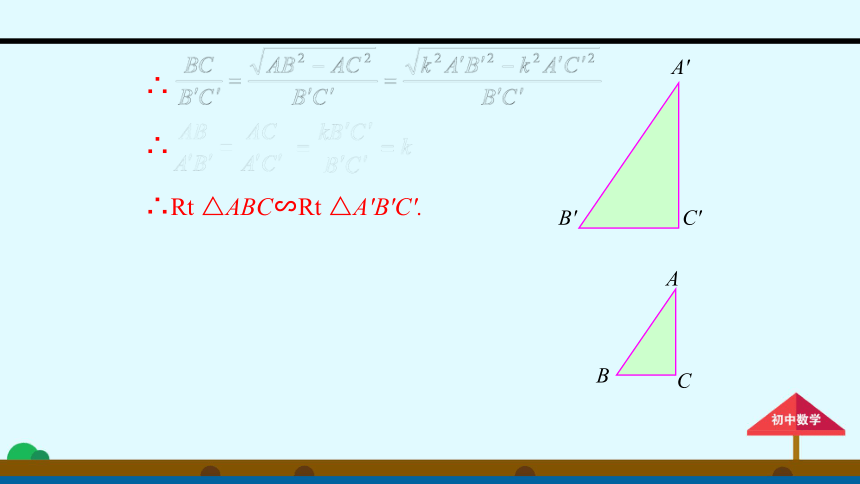
证明:设
由勾股定理
,得
在Rt△ABC和Rt△A′B′C′中∠C=90°,∠C′=90°.
,求证:
Rt△ABC∽Rt△A′B′C′.
A'
B'
C'
A
B
C
合作探究
∴
∴
∴Rt
△ABC∽Rt
△A′B′C′.
A'
B'
C'
A
B
C
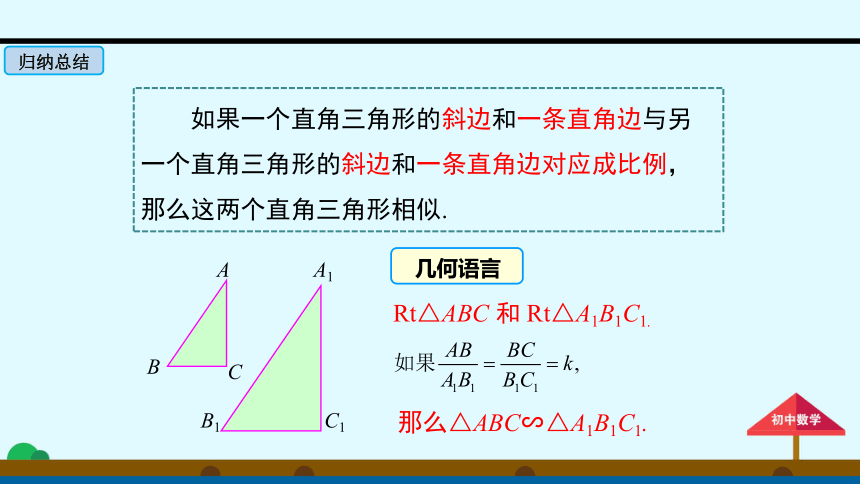
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,
那么这两个直角三角形相似.
A
B
C
那么△ABC∽△A1B1C1.
A1
B1
C1
Rt△ABC
和
Rt△A1B1C1.
几何语言
归纳总结
例1
如图,在Rt△ABC中,∠ABC=90°,AB=4,AC=5.在Rt△A′B′C′中,∠A′C′B′=90°,A′C′=6,A′B′=10.
求证:△ABC∽△B′C′A′.
证明:在Rt△ABC中,
又∵∠ABC=∠A′C′B′=90°,
∴Rt△ABC∽Rt△B′C′A′.
典例精析
例2
如图,下列四个三角形中,与△ABC相似的是(
)
【解析】设网格的边长是1,则
所以AB:AC:BC=1:2:
∴△ABC是直角形三角,且AB∶AC=1∶2,
∵选项A、D选项不是直角三角形,∴排除A、D选项;∵B选项中的三角形的两直角边的边长比为1∶2,
C选项中的三角形的两直角边的边长比为3∶2,
∴选项B正确.
B
以网格图考查的题目,要应用勾股定理分别求出各图形的三角形的三边之比,这是解题的关键.
归纳总结
例3
如图,∠ABC=∠CDB=90°,CB=a,AC=b.问当BD与a,b之间满足怎样的函数表达式时,以点A,B,C为顶点的三角形与以C,D,B为顶点的三角形相似?
解:∵∠ABC=∠CDB=90°,
当
时,△ABC∽△CDB.
当
时,△ABC∽△BDC.
∴
解:∵
ED⊥AB,∴∠EDA=90
°
.
又∠C=90
°,∠A=∠A,
∴
△AED
∽△ABC.
例4
如图,在
Rt△ABC
中,∠C
=
90°,AB
=
10,AC
=
8.
E
是
AC
上一点,AE
=
5,ED⊥AB,垂足为D.
求AD的长.
D
A
B
C
E
∴
由此得到一个判定直角三角形相似的方法:
有一个锐角相等的两个直角三角形相似.
归纳总结
1.在Rt△ABC和Rt△A′B′C′中,已知∠C=∠C′=90°.依据下列各组条件判定这两个三角形是不是相似,并说明理由.
(1)∠A=25°,∠B′=65°;
解:(1)∵
∠A=25°,∠C=90°,
∴
∠B=65°,
∴
∠B=∠B′=65°,
∠C=∠C′=90°,
∴
Rt△ABC∽Rt△A′B′C′.
巩固练习
(2)∵AC=3,BC=4,A′C′=6,B′C′=8,
且∠C=∠C′=90°,
∴
Rt△ABC∽Rt△A′B′C′.
(2)AC=3,BC=4,A′C′=6,B′C′=8;
2.如图,已知Rt△ABC和Rt△A′B′C′中∠A=∠A′=90°,AD,A′D′分别是两个三角形斜边上的高,且CD∶C′D′=AC∶A′C′
请说明:△ABC∽△A′B′C′.
相似图形三角形的判定方法:
通过定义
平行于三角形一边的直线
两角分别相等
两边对应成比例且夹角相等
三边对应成比
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(AA)
(SAS)
(HL)
(SSS)
本节小结
第22章
相似形
沪科版数学九年级上册
第22章
相似形
沪科版数学九年级上册
22.2
相似三角形的判定
第5课时
判定两个直角三角形相似
1.掌握直角三角形相似的判定;(重点)
2.能熟练地运用直角三角形相似的判定定理.(难点)
学习目标
本节目标
观察两副三角尺如图,其中同样角度(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.一般地,如果两个三角形有两组对应角相等,它们一定相似吗?对于直角三角形,类似于判定三角形全等的HL方法,我们能不能通过两边来判断两个三角形相似呢?
引入新知
观察思考
画一画:在下图的边长为1的方格上任画一个直角三角形,再画出第二个三角形,使它的一直角边和斜边长都是原三角形的对应边长的两倍.
画完之后,用量角器比较两个
三角形的对应角,你发现了什
么结论?大家的结论都一
样吗?
B
C
A
F
E
D
发现这两个三角形相似.
利用边判定直角三角形相似
新知讲解
证明:设
由勾股定理
,得
在Rt△ABC和Rt△A′B′C′中∠C=90°,∠C′=90°.
,求证:
Rt△ABC∽Rt△A′B′C′.
A'
B'
C'
A
B
C
合作探究
∴
∴
∴Rt
△ABC∽Rt
△A′B′C′.
A'
B'
C'
A
B
C
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,
那么这两个直角三角形相似.
A
B
C
那么△ABC∽△A1B1C1.
A1
B1
C1
Rt△ABC
和
Rt△A1B1C1.
几何语言
归纳总结
例1
如图,在Rt△ABC中,∠ABC=90°,AB=4,AC=5.在Rt△A′B′C′中,∠A′C′B′=90°,A′C′=6,A′B′=10.
求证:△ABC∽△B′C′A′.
证明:在Rt△ABC中,
又∵∠ABC=∠A′C′B′=90°,
∴Rt△ABC∽Rt△B′C′A′.
典例精析
例2
如图,下列四个三角形中,与△ABC相似的是(
)
【解析】设网格的边长是1,则
所以AB:AC:BC=1:2:
∴△ABC是直角形三角,且AB∶AC=1∶2,
∵选项A、D选项不是直角三角形,∴排除A、D选项;∵B选项中的三角形的两直角边的边长比为1∶2,
C选项中的三角形的两直角边的边长比为3∶2,
∴选项B正确.
B
以网格图考查的题目,要应用勾股定理分别求出各图形的三角形的三边之比,这是解题的关键.
归纳总结
例3
如图,∠ABC=∠CDB=90°,CB=a,AC=b.问当BD与a,b之间满足怎样的函数表达式时,以点A,B,C为顶点的三角形与以C,D,B为顶点的三角形相似?
解:∵∠ABC=∠CDB=90°,
当
时,△ABC∽△CDB.
当
时,△ABC∽△BDC.
∴
解:∵
ED⊥AB,∴∠EDA=90
°
.
又∠C=90
°,∠A=∠A,
∴
△AED
∽△ABC.
例4
如图,在
Rt△ABC
中,∠C
=
90°,AB
=
10,AC
=
8.
E
是
AC
上一点,AE
=
5,ED⊥AB,垂足为D.
求AD的长.
D
A
B
C
E
∴
由此得到一个判定直角三角形相似的方法:
有一个锐角相等的两个直角三角形相似.
归纳总结
1.在Rt△ABC和Rt△A′B′C′中,已知∠C=∠C′=90°.依据下列各组条件判定这两个三角形是不是相似,并说明理由.
(1)∠A=25°,∠B′=65°;
解:(1)∵
∠A=25°,∠C=90°,
∴
∠B=65°,
∴
∠B=∠B′=65°,
∠C=∠C′=90°,
∴
Rt△ABC∽Rt△A′B′C′.
巩固练习
(2)∵AC=3,BC=4,A′C′=6,B′C′=8,
且∠C=∠C′=90°,
∴
Rt△ABC∽Rt△A′B′C′.
(2)AC=3,BC=4,A′C′=6,B′C′=8;
2.如图,已知Rt△ABC和Rt△A′B′C′中∠A=∠A′=90°,AD,A′D′分别是两个三角形斜边上的高,且CD∶C′D′=AC∶A′C′
请说明:△ABC∽△A′B′C′.
相似图形三角形的判定方法:
通过定义
平行于三角形一边的直线
两角分别相等
两边对应成比例且夹角相等
三边对应成比
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(AA)
(SAS)
(HL)
(SSS)
本节小结
第22章
相似形
沪科版数学九年级上册
