沪科版数学九年级上册22.3 第1课时 相似三角形的性质定理1、2课件(39张)
文档属性
| 名称 | 沪科版数学九年级上册22.3 第1课时 相似三角形的性质定理1、2课件(39张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 08:38:57 | ||
图片预览





文档简介
(共39张PPT)
第22章
相似形
沪科版数学九年级上册
22.3
相似三角形的性质
第1课时
相似三角形的性质定理1、2
1.明确相似三角形中对应线段与相似比的关系.
(重点)
2.掌握相似三角形的周长比等于相似比及其在实际中的应用.
2.能熟练运用相似三角形的性质解决实际问题.(难点)
学习目标
本节目标
A
C
B
A1
C1
B1
问题1:
△ABC与△A1B1C1相似吗?
引入新知
A
C
B
A1
C1
B1
相似三角形对应角相等、对应边成比例.
△ABC∽
△A1B1C1
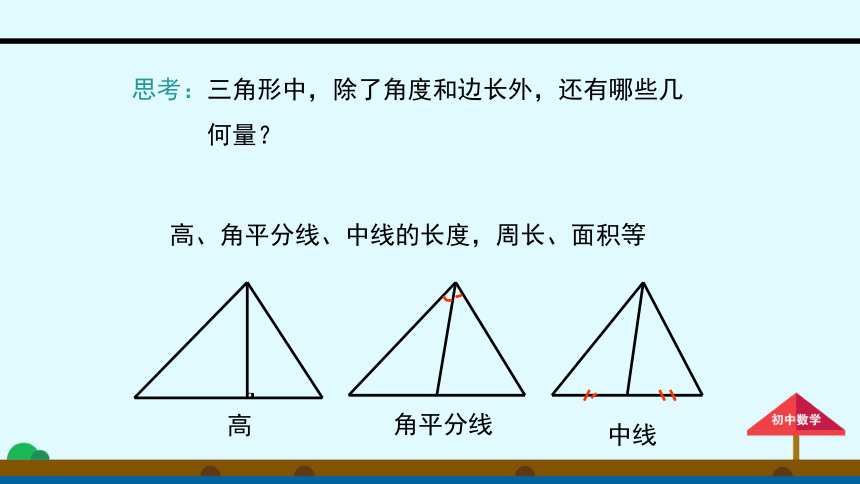
思考:三角形中,除了角度和边长外,还有哪些几
何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
D1
A1
C1
B1
∟
A
C
B
D
∟
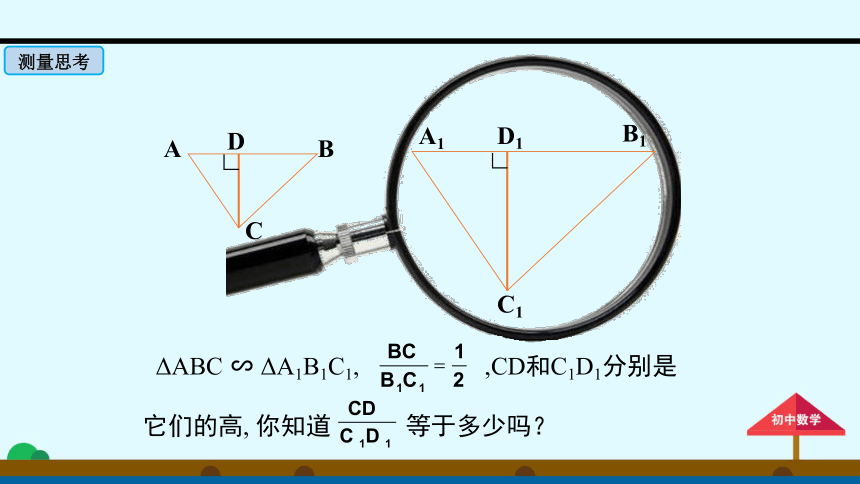
ΔABC
∽
ΔA1B1C1,
,CD和C1D1分别是它们的高,
你知道
等于多少吗?
测量思考
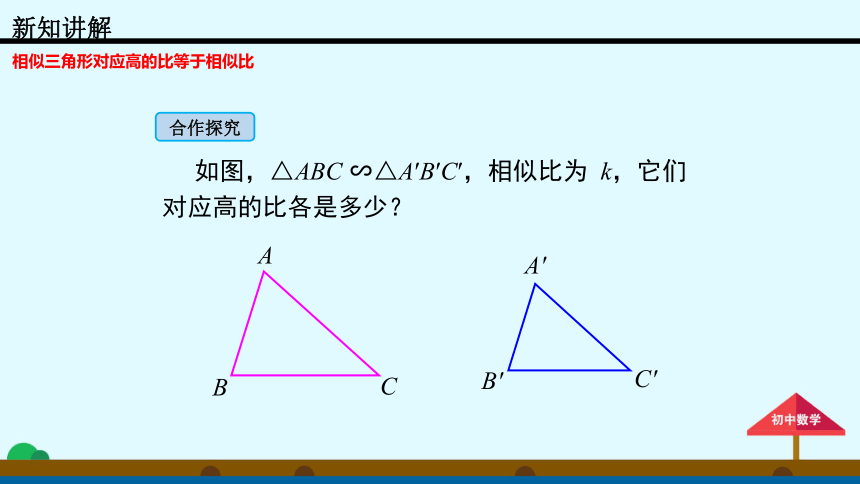
如图,△ABC
∽△A′B′C′,相似比为
k,它们对应高的比各是多少?
A
B
C
A'
B'
C'
相似三角形对应高的比等于相似比
新知讲解
合作探究
∵△ABC
∽△A′B′C′,
∴∠B=∠B'
,
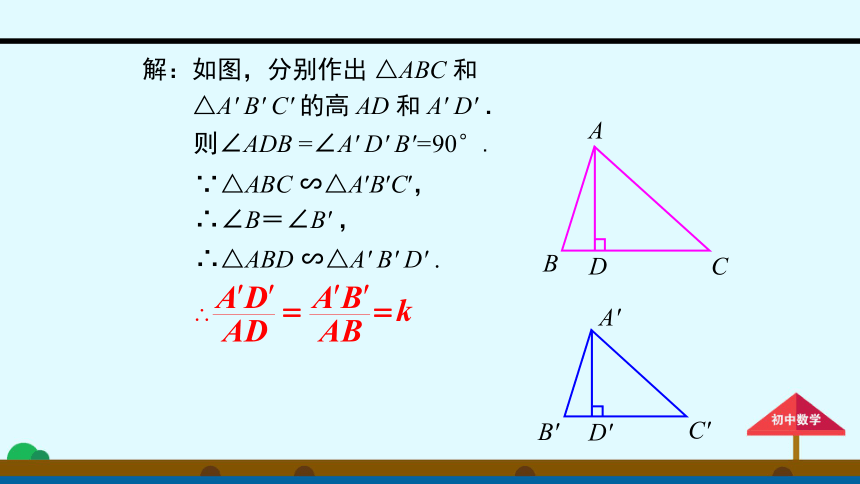
解:如图,分别作出
△ABC
和
△A'
B'
C'
的高
AD
和
A'
D'
.
则∠ADB
=∠A'
D'
B'=90°.
∴△ABD
∽△A'
B'
D'
.
A
B
C
A'
B'
C'
D'
D
由此得到:
相似三角形对应高的比等于相似比.
类似的,我们可以得到其余两组对应边上的高的比也等于相似比.
归纳总结
ΔABC∽
ΔA1B1C1
,BD和B1D1是它们的中线,
已知
,B1D1
=4cm,则BD=
cm.
6
2.ΔABC∽
ΔA1B1C1,
AD和A1D1是对应角平分
线,已知AD=8cm,
A1D1=3cm
,则
ΔABC与
ΔA1B1C1的对应高之比为
.
8:3
随堂练习
3.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是
m.
P
A
D
B
C
2
4
1.5
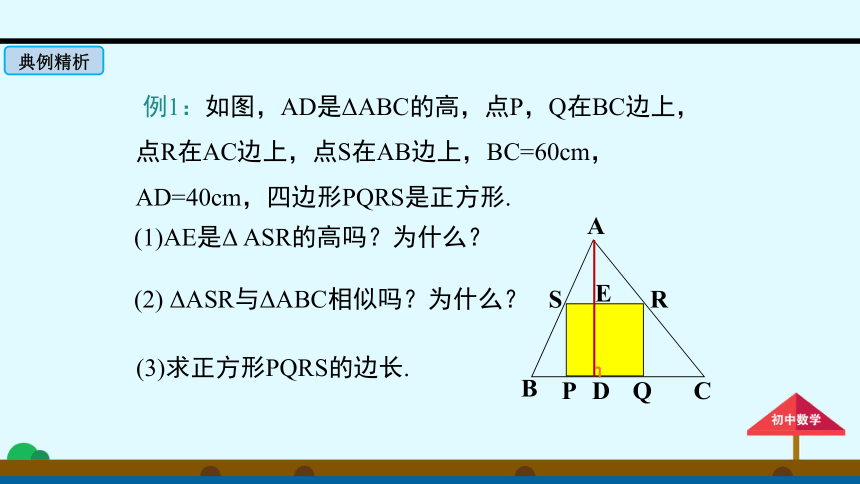
例1:如图,AD是ΔABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.
(1)AE是Δ
ASR的高吗?为什么?
(2)
ΔASR与ΔABC相似吗?为什么?
(3)求正方形PQRS的边长.
S
R
Q
P
E
D
C
B
A
典例精析
(1)AE是ΔASR的高吗?为什么?
解:
AE是ΔASR的高.
理由:
∵AD是ΔABC的高
∴
∠ADC=90°
∵四边形PQRS是正方形
∴SR∥BC
∴∠AER=∠ADC=90°
∴
AE是ΔASR的高.
BC=60cm,AD=40cm,四边形PQRS是正方形.
S
R
Q
P
E
D
C
B
A
BC=60cm,AD=40cm,四边形PQRS是正方形.
(2)
ΔASR与ΔABC相似吗?为什么?
解:
ΔASR与ΔABC相似.
理由:
∵
SR∥BC
∴
∠ASR=∠B,
∠ARS=∠C
∴
ΔASR与ΔABC相似.
S
R
Q
P
E
D
C
B
A
(3)求正方形PQRS的边长.
是方程思想哦!
解:∵
ΔASR
∽
ΔABC
AE、AD分别是ΔASR
和ΔABC
对应边上的高
∴
设正方形PQRS的边长为
x
cm,
则SR=DE=x
cm,AE=(40-x)cm
∴
解得:x=24
∴正方形PQRS的边长为24cm.
S
R
Q
P
E
D
C
B
A
变式:
如图,AD是ΔABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=5cm,AD=10cm,若矩形PQRS的长是宽的2倍,你能求出这个矩形的面积吗?
S
R
Q
P
E
D
C
B
A
如图,AD是ΔABC的高,BC=5cm,AD=10cm.
设SP=xcm,则SR=2x
cm
得到:
所以
x=2
2x=4
S矩形PQRS=
2×4=8cm2
S
R
Q
P
E
D
C
B
A
分析:
情况一:SR=2SP
设SR=xcm,则SP=2x
cm
得到:
所以
x=2.5
2x=5
S矩形PQRS=2.5×5=12.5cm2
原来是分类思想呀!
S
R
Q
P
E
D
C
B
A
分析:
情况二:SP=2SR
如图,AD是ΔABC的高,BC=5cm,AD=10cm
例2:如图,一块铁皮呈锐角三角形,它的边长BC=80cm,高AD=60cm,要把该铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形的边长.
S
R
Q
P
E
D
C
B
A
解
如图,矩形PQRS为加工后的零件,边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E.设PS=xcm,则PQ为2xcm.
S
R
Q
P
E
D
C
B
A
∵PQ∥BC,
∴∠APQ=∠ABC,∠AQP=∠ACB,
∴△APQ∽△ABC.
解方程,得x=24,2x=48.
答:这个矩形的零件的边长分别是48cm和24cm.
问题:把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
图中△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
A
B
C
D
E
A'
B'
D'
C'
E'
相似三角形对应角平分线的比、对应中线的比都等于相似比
已知:△ABC∽△A′B′C′,相似比为k,
求证:
证明:∵
△ABC∽△A′B′C′.
∴
∠B′=
∠B,
.
又AD,AD′分别为对应边的中线.
∴
△ABD∽△A′B′D′.
A'
B'
D'
C'
E'
A
B
C
D
E
猜想验证1
由此得到:
相似三角形对应的中线的比也等于相似比.
同学们可以试着自己用同样的方法求证三角形对应边上的角平分中线的比等于相似比.
归纳总结
已知:△ABC∽△A′B′C′,相似比为k,即
求证:
证明:∵
△ABC∽△A′B′C′
∴
∠B′=
∠B,
∠B′A′C′=
∠BAC.
又AD,AD′分别为对应角的平方线
∴
△ABD∽△A′B′D′.
A'
B'
D'
C'
E'
A
B
C
D
E
猜想验证2
相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
归纳总结
例2:两个相似三角形的两条对应边的长分别是6cm和8cm,如果它们对应的两条角平分线的和为42cm,那么这两条角平分线的长分别是多少?
解:设较短的角平分线长为xcm,
则由相似性质有
.
解得x=18.
较长的角平分线长为24cm.
故这两条角平分线的长分别为18cm,24cm.
问题:图中(1)(2)(3)分别是边长为1,2,3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
(1)与(2)的相似比=______,
(1)与(2)的周长比=______,
(1)与(3)的相似比=______,
(1)与(3)的周长比=______.
1∶
2
结论:
相似三角形的周长比等于______.
相似比
(都相似)
1∶
3
1∶
2
1∶
3
有什么规律吗?
相似三角形周长比等于相似比
证明:设△ABC∽△A1B1C1,相似比为k,
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
想一想:怎么证明这一结论呢?
相似三角形周长的比等于相似比.
归纳总结
∴
△DEF∽△ABC,相似比为
∴△DEF的周长=
△ABC的周长,
△DEF的周长=12.
例3.如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,求△DEF的周长.
A
B
C
D
E
F
又
∠D=∠A
解:在△ABC和△DEF中,
∵
AB=2DE,AC=2DF
∴
3.两个相似三角形对应中线的比为
,
则对应高的比为______
.
2.相似三角形对应边的比为2∶3,那么对应角的角平分线的比为______.
2∶
3
1.两个相似三角形的相似比为
,
则对应高的比为_________,
则对应中线的比为_________.
巩固练习
解:∵
△ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2cm.
A
G
B
C
D
E
F
H
4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
5.
若△ABC
∽△
A′B′C′
,它们的周长分别为60cm和72cm,且AB=15cm,B′C′=24cm,求BC,AC,A′B′,A′C′的长.
B
A
C
解:∵
△ABC
∽△
A′B′C′
,它们的周长分别为60cm和72cm,
∵AB=15cm,B′C′=24cm,
∴BC
=
20cm,
AC
=
25cm,
A′B′=18cm,A′C′=30cm.
6.如图,AD是△ABC的高,AD=h,
点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当
时,求DE的长.如果
呢?
∴△ASR∽△ABC
(两角分别相等的两个三角形相似).
解:∵SR⊥AD,BC⊥AD,
B
A
E
R
C
D
S
∴SR∥BC.
∴∠ASR=∠B,∠ARS=∠C.
(相似三角形对应高的比等于相似比),
当
时,得
解得
B
A
E
R
C
D
S
当
时,得
解得
7.
一块直角三角形木板的一条直角边AB长为1.5m,面积为1.5m2,要把它加工成一个面积尽可能大的正方形桌面,甲乙两位同学的加工方法如图(1)、(2)所示,请你用学过的知识说明哪位同学的加工方法更好。(加工损耗忽略不计,计算结果中的分数可保留)
F
A
B
C
D
E
(1)
F
G
B
A
C
E
D
(2)
相信自己是最棒的!
拓展提高
S
R
Q
P
E
D
C
B
A
8.AD是ΔABC的高,BC=60cm,AD=40cm,求图中小正方形的边长.
A
C
B
D
(1)
A
C
B
D
(5)
D
C
B
A
(4)
A
C
B
D
(3)
D
C
B
A
(1)
A
C
B
D
(2)
相似三角形的性质
相似三角形对应高的比、对应中线的比和对应角平分线的比等于相似比
相似三角形周长之比等于相似比
本节小结
第22章
相似形
沪科版数学九年级上册
第22章
相似形
沪科版数学九年级上册
22.3
相似三角形的性质
第1课时
相似三角形的性质定理1、2
1.明确相似三角形中对应线段与相似比的关系.
(重点)
2.掌握相似三角形的周长比等于相似比及其在实际中的应用.
2.能熟练运用相似三角形的性质解决实际问题.(难点)
学习目标
本节目标
A
C
B
A1
C1
B1
问题1:
△ABC与△A1B1C1相似吗?
引入新知
A
C
B
A1
C1
B1
相似三角形对应角相等、对应边成比例.
△ABC∽
△A1B1C1
思考:三角形中,除了角度和边长外,还有哪些几
何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
D1
A1
C1
B1
∟
A
C
B
D
∟
ΔABC
∽
ΔA1B1C1,
,CD和C1D1分别是它们的高,
你知道
等于多少吗?
测量思考
如图,△ABC
∽△A′B′C′,相似比为
k,它们对应高的比各是多少?
A
B
C
A'
B'
C'
相似三角形对应高的比等于相似比
新知讲解
合作探究
∵△ABC
∽△A′B′C′,
∴∠B=∠B'
,
解:如图,分别作出
△ABC
和
△A'
B'
C'
的高
AD
和
A'
D'
.
则∠ADB
=∠A'
D'
B'=90°.
∴△ABD
∽△A'
B'
D'
.
A
B
C
A'
B'
C'
D'
D
由此得到:
相似三角形对应高的比等于相似比.
类似的,我们可以得到其余两组对应边上的高的比也等于相似比.
归纳总结
ΔABC∽
ΔA1B1C1
,BD和B1D1是它们的中线,
已知
,B1D1
=4cm,则BD=
cm.
6
2.ΔABC∽
ΔA1B1C1,
AD和A1D1是对应角平分
线,已知AD=8cm,
A1D1=3cm
,则
ΔABC与
ΔA1B1C1的对应高之比为
.
8:3
随堂练习
3.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是
m.
P
A
D
B
C
2
4
1.5
例1:如图,AD是ΔABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.
(1)AE是Δ
ASR的高吗?为什么?
(2)
ΔASR与ΔABC相似吗?为什么?
(3)求正方形PQRS的边长.
S
R
Q
P
E
D
C
B
A
典例精析
(1)AE是ΔASR的高吗?为什么?
解:
AE是ΔASR的高.
理由:
∵AD是ΔABC的高
∴
∠ADC=90°
∵四边形PQRS是正方形
∴SR∥BC
∴∠AER=∠ADC=90°
∴
AE是ΔASR的高.
BC=60cm,AD=40cm,四边形PQRS是正方形.
S
R
Q
P
E
D
C
B
A
BC=60cm,AD=40cm,四边形PQRS是正方形.
(2)
ΔASR与ΔABC相似吗?为什么?
解:
ΔASR与ΔABC相似.
理由:
∵
SR∥BC
∴
∠ASR=∠B,
∠ARS=∠C
∴
ΔASR与ΔABC相似.
S
R
Q
P
E
D
C
B
A
(3)求正方形PQRS的边长.
是方程思想哦!
解:∵
ΔASR
∽
ΔABC
AE、AD分别是ΔASR
和ΔABC
对应边上的高
∴
设正方形PQRS的边长为
x
cm,
则SR=DE=x
cm,AE=(40-x)cm
∴
解得:x=24
∴正方形PQRS的边长为24cm.
S
R
Q
P
E
D
C
B
A
变式:
如图,AD是ΔABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=5cm,AD=10cm,若矩形PQRS的长是宽的2倍,你能求出这个矩形的面积吗?
S
R
Q
P
E
D
C
B
A
如图,AD是ΔABC的高,BC=5cm,AD=10cm.
设SP=xcm,则SR=2x
cm
得到:
所以
x=2
2x=4
S矩形PQRS=
2×4=8cm2
S
R
Q
P
E
D
C
B
A
分析:
情况一:SR=2SP
设SR=xcm,则SP=2x
cm
得到:
所以
x=2.5
2x=5
S矩形PQRS=2.5×5=12.5cm2
原来是分类思想呀!
S
R
Q
P
E
D
C
B
A
分析:
情况二:SP=2SR
如图,AD是ΔABC的高,BC=5cm,AD=10cm
例2:如图,一块铁皮呈锐角三角形,它的边长BC=80cm,高AD=60cm,要把该铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形的边长.
S
R
Q
P
E
D
C
B
A
解
如图,矩形PQRS为加工后的零件,边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E.设PS=xcm,则PQ为2xcm.
S
R
Q
P
E
D
C
B
A
∵PQ∥BC,
∴∠APQ=∠ABC,∠AQP=∠ACB,
∴△APQ∽△ABC.
解方程,得x=24,2x=48.
答:这个矩形的零件的边长分别是48cm和24cm.
问题:把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
图中△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
A
B
C
D
E
A'
B'
D'
C'
E'
相似三角形对应角平分线的比、对应中线的比都等于相似比
已知:△ABC∽△A′B′C′,相似比为k,
求证:
证明:∵
△ABC∽△A′B′C′.
∴
∠B′=
∠B,
.
又AD,AD′分别为对应边的中线.
∴
△ABD∽△A′B′D′.
A'
B'
D'
C'
E'
A
B
C
D
E
猜想验证1
由此得到:
相似三角形对应的中线的比也等于相似比.
同学们可以试着自己用同样的方法求证三角形对应边上的角平分中线的比等于相似比.
归纳总结
已知:△ABC∽△A′B′C′,相似比为k,即
求证:
证明:∵
△ABC∽△A′B′C′
∴
∠B′=
∠B,
∠B′A′C′=
∠BAC.
又AD,AD′分别为对应角的平方线
∴
△ABD∽△A′B′D′.
A'
B'
D'
C'
E'
A
B
C
D
E
猜想验证2
相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
归纳总结
例2:两个相似三角形的两条对应边的长分别是6cm和8cm,如果它们对应的两条角平分线的和为42cm,那么这两条角平分线的长分别是多少?
解:设较短的角平分线长为xcm,
则由相似性质有
.
解得x=18.
较长的角平分线长为24cm.
故这两条角平分线的长分别为18cm,24cm.
问题:图中(1)(2)(3)分别是边长为1,2,3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
(1)与(2)的相似比=______,
(1)与(2)的周长比=______,
(1)与(3)的相似比=______,
(1)与(3)的周长比=______.
1∶
2
结论:
相似三角形的周长比等于______.
相似比
(都相似)
1∶
3
1∶
2
1∶
3
有什么规律吗?
相似三角形周长比等于相似比
证明:设△ABC∽△A1B1C1,相似比为k,
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
想一想:怎么证明这一结论呢?
相似三角形周长的比等于相似比.
归纳总结
∴
△DEF∽△ABC,相似比为
∴△DEF的周长=
△ABC的周长,
△DEF的周长=12.
例3.如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,求△DEF的周长.
A
B
C
D
E
F
又
∠D=∠A
解:在△ABC和△DEF中,
∵
AB=2DE,AC=2DF
∴
3.两个相似三角形对应中线的比为
,
则对应高的比为______
.
2.相似三角形对应边的比为2∶3,那么对应角的角平分线的比为______.
2∶
3
1.两个相似三角形的相似比为
,
则对应高的比为_________,
则对应中线的比为_________.
巩固练习
解:∵
△ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2cm.
A
G
B
C
D
E
F
H
4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
5.
若△ABC
∽△
A′B′C′
,它们的周长分别为60cm和72cm,且AB=15cm,B′C′=24cm,求BC,AC,A′B′,A′C′的长.
B
A
C
解:∵
△ABC
∽△
A′B′C′
,它们的周长分别为60cm和72cm,
∵AB=15cm,B′C′=24cm,
∴BC
=
20cm,
AC
=
25cm,
A′B′=18cm,A′C′=30cm.
6.如图,AD是△ABC的高,AD=h,
点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当
时,求DE的长.如果
呢?
∴△ASR∽△ABC
(两角分别相等的两个三角形相似).
解:∵SR⊥AD,BC⊥AD,
B
A
E
R
C
D
S
∴SR∥BC.
∴∠ASR=∠B,∠ARS=∠C.
(相似三角形对应高的比等于相似比),
当
时,得
解得
B
A
E
R
C
D
S
当
时,得
解得
7.
一块直角三角形木板的一条直角边AB长为1.5m,面积为1.5m2,要把它加工成一个面积尽可能大的正方形桌面,甲乙两位同学的加工方法如图(1)、(2)所示,请你用学过的知识说明哪位同学的加工方法更好。(加工损耗忽略不计,计算结果中的分数可保留)
F
A
B
C
D
E
(1)
F
G
B
A
C
E
D
(2)
相信自己是最棒的!
拓展提高
S
R
Q
P
E
D
C
B
A
8.AD是ΔABC的高,BC=60cm,AD=40cm,求图中小正方形的边长.
A
C
B
D
(1)
A
C
B
D
(5)
D
C
B
A
(4)
A
C
B
D
(3)
D
C
B
A
(1)
A
C
B
D
(2)
相似三角形的性质
相似三角形对应高的比、对应中线的比和对应角平分线的比等于相似比
相似三角形周长之比等于相似比
本节小结
第22章
相似形
沪科版数学九年级上册
