沪科版数学九年级上册23.2 第3课时 方向角问题(27张PPT)
文档属性
| 名称 | 沪科版数学九年级上册23.2 第3课时 方向角问题(27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 689.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-24 07:32:37 | ||
图片预览





文档简介
(共27张PPT)
第23章
解直角三角形
沪科版数学九年级上册
23.2
解直角三角形及其应用
第3课时
方向角问题
1.正确理解方向角的概念;(重点)
2.能运用解直角三角形知识解决方向角的问题.
(难点)
学习目标
本节目标
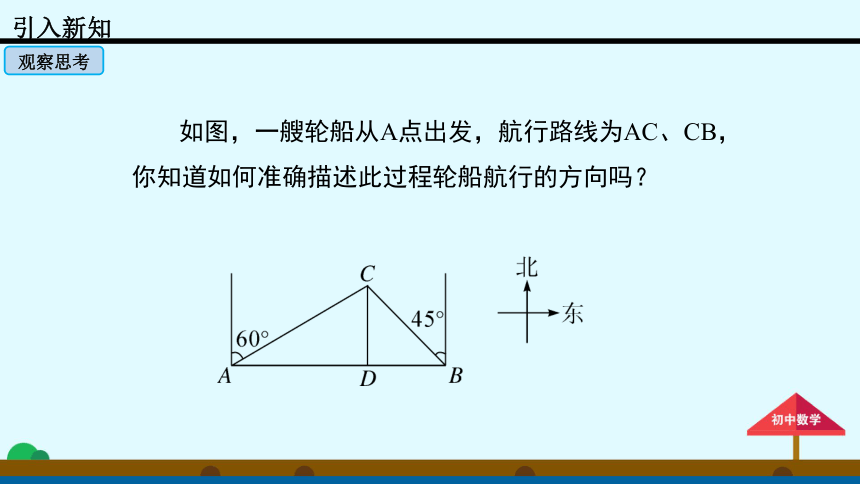
如图,一艘轮船从A点出发,航行路线为AC、CB,你知道如何准确描述此过程轮船航行的方向吗?
引入新知
观察思考
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角.
如图所示:
30°
45°
B
O
A
东
西
北
南
45°
45°
西南
O
东北
东
西
北
南
西北
东南
北偏东30°
南偏西45°
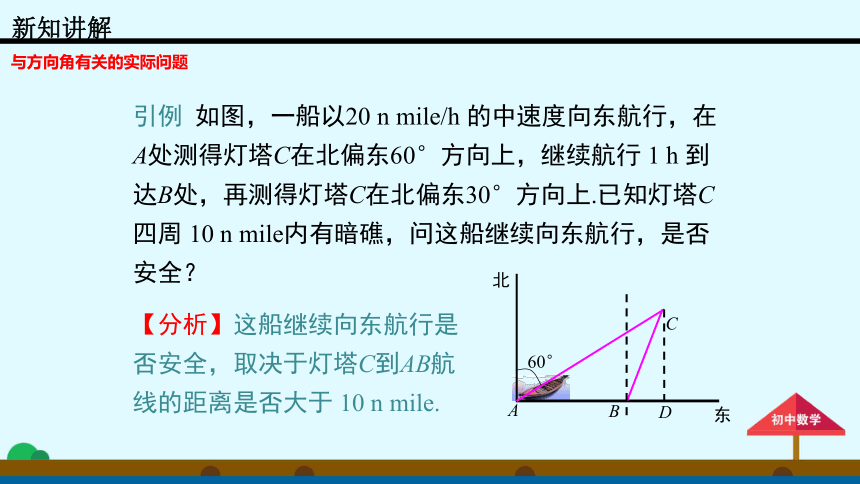
引例
如图,一船以20
n
mile/h
的中速度向东航行,在A处测得灯塔C在北偏东60°方向上,继续航行
1
h
到达B处,再测得灯塔C在北偏东30°方向上.已知灯塔C四周
10
n
mile内有暗礁,问这船继续向东航行,是否安全?
A
C
B
60°
D
【分析】这船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于
10
n
mile.
北
东
与方向角有关的实际问题
新知讲解
解:由点C作CD⊥AB,
设CD=
x
,
则在Rt△ACD中,
在Rt△BCD中,
解得
所以,这船继续向东航行是安全的.
A
C
B
D
30°
60°
北
东
由AB=AD-CD,得
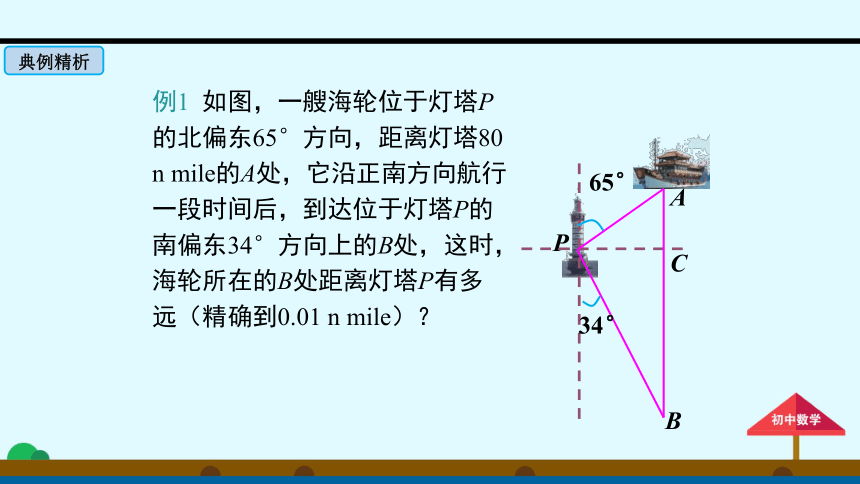
例1
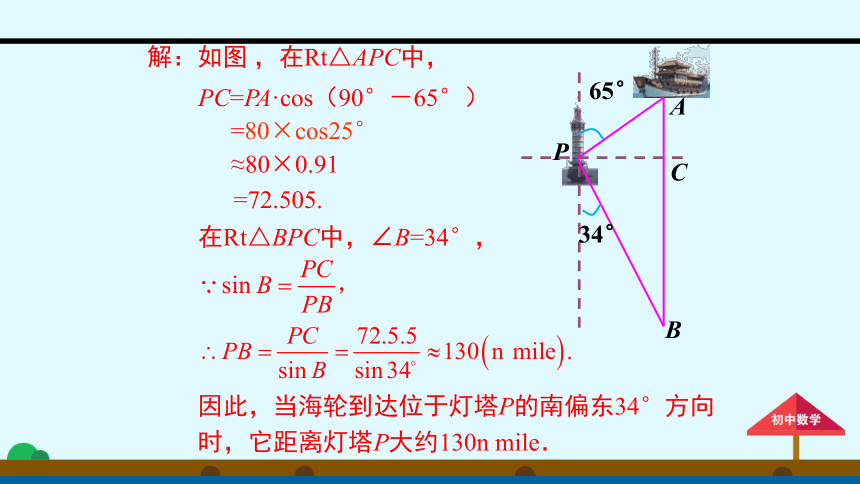
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80
n
mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01
n
mile)?
65°
34°
P
B
C
A
典例精析
解:如图
,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.505.
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向
时,它距离灯塔P大约130n
mile.
65°
34°
P
B
C
A
如图所示,A、B两城市相距200km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,100km为半径的圆形区
域内,请问:计划修
筑的这条高速公路会
不会穿越保护区(参考
数据:
≈1.732,
≈1.414).
200km
随堂演练
200km
解:过点P作PC⊥AB,C是垂足.
则∠APC=30°,∠BPC=45°,
AC=PC·tan30°,BC=PC·tan45°.
∵AC+BC=AB,
∴PC
·
tan30°+PC
·
tan45°=200,
即
PC+PC=200,
解得
PC≈126.8km>100km.
答:计划修筑的这条高速公
路不会穿越保护区.
C
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
知识总结
例2
一条东西走向的高速公路上有两个加油站A,B,在A的北偏东45°方向还有一个加油站C,C到高速公路的最短距离是30km,B,C间的距离是60km,想要经过C修一条笔直的公路与高速公路相交,使两路交叉口P到B,C的距离相等,请求出交叉口P到加油站A的距离(结果保留根号).
分析:此题针对点P的位置分两种情况讨论,即点P可能在线段AB上,也可能在BA的延长线上.
解:分两种情况:
(1)如图①,在Rt△BDC中,CD=30km,BC=60km,
∴∠B=30°.
∵PB=PC,∴∠BCP=∠B=30°.
∴在Rt△CDP中,∠CPD=∠B+∠BCP=60°.
在Rt△ADC中,∵∠A=45°,
∴AD=DC=30km.
(2)如图②,同理可求得
km,
AD=30km.
求一般三角形的边长或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
知识总结
例3
如图,一架飞机从A地飞往B地,两地相距600km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成30°角的方向飞行,飞行到中途,再沿与原来的飞行方向成45°角的方向继续飞行直到终点.这样飞机的飞行路程比原来的路程600km远了多少?
解:过点C作CD⊥AB于点D,
∵AD+BD=AB,
∴在Rt△BCD中,
∴AC+BC=
在Rt△ACD中,
747-600=147(km).
答:飞机的飞行路程比原来的路程600km远了147km.
求一般三角形的边长或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
知识总结
1.
如图,某渔船如图所示,某渔船在海面上朝正东方
向匀速航行,在A处观测到灯塔M在北偏东60°方
向上,航行半小时后到达B处,此时观测到灯塔M
在北偏东30°方向上,那么该船继续航行到达离灯
塔距离最近的位置所需的时间是
(
)
A.
10分钟
B.
15分钟
C.
20分钟
D.
25分钟
B
巩固练习
2.
如图,C岛在A岛的北偏东50°方向,C岛在B岛的
北偏西40°方向,则从C岛看A,B两岛的视角
∠ACB等于
.
90°
3.
如图,海上B、C两岛分别位于A岛的正东和正北方
向,一艘船从A岛出发,以18海里/时的速度向正北
方向航行2小时到达C岛,此时测得B岛在C岛的南
偏东43°方向,则A、B两岛之间的距离为
.
(结果精确到0.1海里,参考数据:sin43°=0.68,
cos43°=0.73,tan43°=0.93)
33.5海里
4.
如图有一个古镇建筑A,它周围800米内有古建筑,
乡村路要由西向东修筑,在B点处测得古建筑A在北
偏东60°方向上,向前直行1200米到达D点,这时
测得古建筑A在D点北偏东30°方向上,如果不改变
修筑的方向,你认为古建筑会不会遭到破坏?
E
答案:AE=
米.
>800,
所以古建筑会遭到破坏.
5.
某海滨浴场东西走向的海岸线可近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号.他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲、乙的游泳速度都是2米/秒,则谁先到达B处?请说明理由.
分析:
在Rt△CDB中,利用三角函数即可求得BC,BD的长,则可求得甲、乙所用的时间,比较二者之间的大小即可.
(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43).
方向角:指北方向或指南方向与目标方向线所成的小于90°的水平角,叫方向角.
解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系.
本节小结
第23章
解直角三角形
沪科版数学九年级上册
第23章
解直角三角形
沪科版数学九年级上册
23.2
解直角三角形及其应用
第3课时
方向角问题
1.正确理解方向角的概念;(重点)
2.能运用解直角三角形知识解决方向角的问题.
(难点)
学习目标
本节目标
如图,一艘轮船从A点出发,航行路线为AC、CB,你知道如何准确描述此过程轮船航行的方向吗?
引入新知
观察思考
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角.
如图所示:
30°
45°
B
O
A
东
西
北
南
45°
45°
西南
O
东北
东
西
北
南
西北
东南
北偏东30°
南偏西45°
引例
如图,一船以20
n
mile/h
的中速度向东航行,在A处测得灯塔C在北偏东60°方向上,继续航行
1
h
到达B处,再测得灯塔C在北偏东30°方向上.已知灯塔C四周
10
n
mile内有暗礁,问这船继续向东航行,是否安全?
A
C
B
60°
D
【分析】这船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于
10
n
mile.
北
东
与方向角有关的实际问题
新知讲解
解:由点C作CD⊥AB,
设CD=
x
,
则在Rt△ACD中,
在Rt△BCD中,
解得
所以,这船继续向东航行是安全的.
A
C
B
D
30°
60°
北
东
由AB=AD-CD,得
例1
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80
n
mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01
n
mile)?
65°
34°
P
B
C
A
典例精析
解:如图
,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.505.
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向
时,它距离灯塔P大约130n
mile.
65°
34°
P
B
C
A
如图所示,A、B两城市相距200km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,100km为半径的圆形区
域内,请问:计划修
筑的这条高速公路会
不会穿越保护区(参考
数据:
≈1.732,
≈1.414).
200km
随堂演练
200km
解:过点P作PC⊥AB,C是垂足.
则∠APC=30°,∠BPC=45°,
AC=PC·tan30°,BC=PC·tan45°.
∵AC+BC=AB,
∴PC
·
tan30°+PC
·
tan45°=200,
即
PC+PC=200,
解得
PC≈126.8km>100km.
答:计划修筑的这条高速公
路不会穿越保护区.
C
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
知识总结
例2
一条东西走向的高速公路上有两个加油站A,B,在A的北偏东45°方向还有一个加油站C,C到高速公路的最短距离是30km,B,C间的距离是60km,想要经过C修一条笔直的公路与高速公路相交,使两路交叉口P到B,C的距离相等,请求出交叉口P到加油站A的距离(结果保留根号).
分析:此题针对点P的位置分两种情况讨论,即点P可能在线段AB上,也可能在BA的延长线上.
解:分两种情况:
(1)如图①,在Rt△BDC中,CD=30km,BC=60km,
∴∠B=30°.
∵PB=PC,∴∠BCP=∠B=30°.
∴在Rt△CDP中,∠CPD=∠B+∠BCP=60°.
在Rt△ADC中,∵∠A=45°,
∴AD=DC=30km.
(2)如图②,同理可求得
km,
AD=30km.
求一般三角形的边长或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
知识总结
例3
如图,一架飞机从A地飞往B地,两地相距600km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成30°角的方向飞行,飞行到中途,再沿与原来的飞行方向成45°角的方向继续飞行直到终点.这样飞机的飞行路程比原来的路程600km远了多少?
解:过点C作CD⊥AB于点D,
∵AD+BD=AB,
∴在Rt△BCD中,
∴AC+BC=
在Rt△ACD中,
747-600=147(km).
答:飞机的飞行路程比原来的路程600km远了147km.
求一般三角形的边长或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
知识总结
1.
如图,某渔船如图所示,某渔船在海面上朝正东方
向匀速航行,在A处观测到灯塔M在北偏东60°方
向上,航行半小时后到达B处,此时观测到灯塔M
在北偏东30°方向上,那么该船继续航行到达离灯
塔距离最近的位置所需的时间是
(
)
A.
10分钟
B.
15分钟
C.
20分钟
D.
25分钟
B
巩固练习
2.
如图,C岛在A岛的北偏东50°方向,C岛在B岛的
北偏西40°方向,则从C岛看A,B两岛的视角
∠ACB等于
.
90°
3.
如图,海上B、C两岛分别位于A岛的正东和正北方
向,一艘船从A岛出发,以18海里/时的速度向正北
方向航行2小时到达C岛,此时测得B岛在C岛的南
偏东43°方向,则A、B两岛之间的距离为
.
(结果精确到0.1海里,参考数据:sin43°=0.68,
cos43°=0.73,tan43°=0.93)
33.5海里
4.
如图有一个古镇建筑A,它周围800米内有古建筑,
乡村路要由西向东修筑,在B点处测得古建筑A在北
偏东60°方向上,向前直行1200米到达D点,这时
测得古建筑A在D点北偏东30°方向上,如果不改变
修筑的方向,你认为古建筑会不会遭到破坏?
E
答案:AE=
米.
>800,
所以古建筑会遭到破坏.
5.
某海滨浴场东西走向的海岸线可近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号.他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲、乙的游泳速度都是2米/秒,则谁先到达B处?请说明理由.
分析:
在Rt△CDB中,利用三角函数即可求得BC,BD的长,则可求得甲、乙所用的时间,比较二者之间的大小即可.
(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43).
方向角:指北方向或指南方向与目标方向线所成的小于90°的水平角,叫方向角.
解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系.
本节小结
第23章
解直角三角形
沪科版数学九年级上册
